A small body tied to one end of the string is whirled in a vertical circle. Find the velocity and tension at the lowest and highest point of the circle respectively. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Let a body of mass (m) attached to one end of a massless and inextensible string. It executes circular motion in a vertical plane with the other end of the string which is fixed. The length of the string becomes the radius $(\to r)$ of the circular path as shown in the figure (motion in vertical circle).

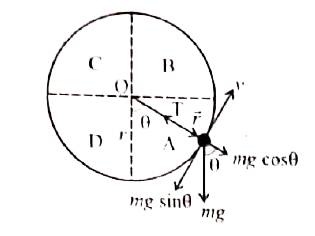
Let us discuss the motion of the body by taking the free body diagram (FBD) at a position where the position vector $(\to r)$ makes an angle $θ$ with the vertically downward direction. The instantaneous velocity is as shown in figure. There are two forces acting on the mass. They are
(i) Gravitational force that acts downward.
(ii) Tension acts along the string.
Applying Newton's second law on the mass, in the tangential direction, we get
$m g sin θ = m a_{1}$
$m g sin θ = - m (\frac{d v}{d t}) ... (1)$
where, $a t = - \frac{d v}{d t}$ is tangential retardation In the radial direction,
$T - m g cos θ = m a_{r}$
$T - m g cos θ = \frac{m v^{2}}{r} ... (2)$
Where, $a_{r} = \frac{v^{2}}{r}$ is the centripetal acceleration
Let the circle can be divided into four sections A, B, C, D for better understanding of the motion. The four important facts to be understood from the two equations are as follows:
(i) The mass is having tangential acceleration $(g sin θ)$ for all values of $θ$ (except $θ = 0^{\circ}$ ), from this it is clear that this vertical circular motion is not a uniform circular motion.
(iii) From the equations (1) and (2) it is understood that as the magnitude of velocity is not a constant in the course of motion, the tension in the string is also not constant.
(iii) The equation (2), $T = m g cos θ + \frac{m v^{2}}{r}$ highlights that in sections A and D of the circle, (for $- \frac{π}{2} < θ < \frac{π}{2}, cos θ$ is positive), the term $m g cos θ$ is always greater than zero. Hence the tension cannot be vanished even when the velocity vanishes.
(iv) The equation (2), $\frac{m v^{2}}{r} = T - m g cos θ$ , further highlights that in sections B and C of the circle, (for $- \frac{π}{2} < θ < \frac{3 π}{2}, cos θ$ is negative) the second term is always greater than zero. Hence velocity cannot be vanished, even when the tension is vanished.
The important points which are to be kept in mind are related to motion in vertical circle.
(a) To start with let us consider only two positions, say the lowest point 1 and the highest point 2 as shown in the figure for further analysis.
(b) Let the velocity of the body at the lowest point 1 be ${\to v}_{1}$ , at the highest point 2 be ${\to v}_{2}$ and $\to v$ at any other point.
(c ) The direction of velocity is tangential to the circular path at all points.
(d) Let ${\to T}_{1}$ be the tension in the string at the lowest point let ${\to T}_{2}$ be the tension at the highest point and $\to T$ be the tension at any other point.
(e) Tension at each point acts towards the centre. The tensions and velocities at these two points can be found by applying the law of conservation of energy.
For the lowest point (1): When the body is at the lowest point 1, the gravitational force $m \to g$ that acts on the body vertically downwards and another one is the tension ${\to T}_{1}$ acting vertically upwards, i.e., towards the centre. From the equation (2), we get
$T_{1} - m g = \frac{m v_{1}^{2}}{r} ... (3)$
$T_{1} = \frac{m v_{1}^{2}}{r} + m g ... (4)$

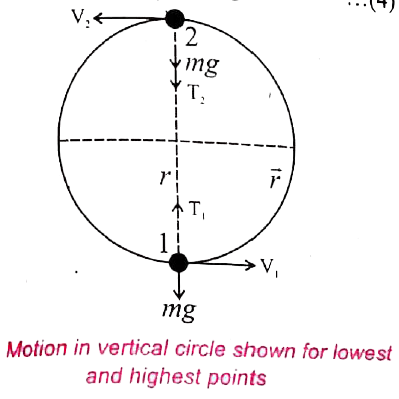
For the highest point (2): At the highest point 2, both the gravitational force $m \to g$ on the body and the tension ${\to T}_{2}$ act downwards, i.e., towards the centre again.
$T_{2} + m g = \frac{m v_{2}^{2}}{r_{2}} ... (5)$
$T_{2} = \frac{m v_{2}^{2}}{r_{2}} - m g ... (6)$
From equations (4) and (5), it is understood that $T_{1} > T_{2}$ .
By subtracting equation (6) from equation (4). The difference in tension $T_{1} - T_{2}$ is obtained.
$T_{1} - T_{2} = \frac{m v_{1}^{2}}{r} + m g - (\frac{m v_{2}^{2}}{r} - m g)$
$= \frac{m v_{1}^{2}}{r} + m g - \frac{m v_{2}^{2}}{r} + m g$
$T_{1} - T_{2} = \frac{m}{r} [v_{1}^{2} - v_{2}^{2}] + 2 m g ... (7)$
The term $[v_{1}^{2} - v_{2}^{2}]$ can be found easily by applying law of conservation of energy at point 1 and also at point 2.
But total energy at point $1 (E_{1})$ is same as the total energy at a point $2 (E_{2})$
$E_{1} = E_{2} ... (8)$
Potential energy at point 1, $U_{1} = 0$ (by taking reference as point 1)
Kinetic energy at point 1,
$K E_{1} = \frac{1}{2} m v_{1}^{2}$
Total energy at point 1,
$E_{1} = U_{1} + K E_{1} = 0 + \frac{1}{2} m v_{1}^{2}$
$= \frac{1}{2} m v_{1}^{2}$
Similarly, potential energy at point 2,
$U_{2} = m g (2 r)$ ( $h = 2 r$ from point 1)
Kinetic energy at point 2,
$K E_{2} = \frac{1}{2} m v_{2}^{2}$
Total energy at pont 2,
$E_{2} = U_{2} + K E_{2} = 2 m g r + \frac{1}{2} m v_{2}^{2}$
From the law of conservation of energy given in equation (8), we get
$\frac{1}{2} m v_{1}^{2} = 2 m g r + \frac{1}{2} m v_{2}^{2}$
After rearranging,
$\frac{1}{2} m [v_{1}^{2} - v_{2}^{2}] = 2 m g r$
$v_{1}^{2} - v_{2}^{2} = 4 g r ... (9)$
Substituting equatoin (9) in equation (7) we get,
$T_{1} - T_{2} = \frac{m}{r} [4 g r] + 2 m g$
Hence, the difference in tension is
$T_{1} - T_{2} = 6 m g$
Minimum speed at the highest point (2): The body must have a minimum speed at point 2 otherwise, the string will slack before reaching point 2. So the body will not loop the circle. To find this minimum speed let us take the tension $T_{2} = 0$ in equation (6).
$0 = \frac{m v_{2}^{2}}{r} - m g \Rightarrow \frac{m v_{2}^{2}}{r} = m g$
$v_{2}^{2} = r g$
$v_{2} = \sqrt{g r} ... (10)$
The body must have a speed at point 2, $v_{2} \geq \sqrt{g r}$ to stay in the circular path.
Minimum speed at the lowest pont 1: To have this minimum speed $(v_{2} = \sqrt{g r})$ at point 2, the body must have minimum speed also at point 1.
By making use of equation (9) we can find the minimum speed at point 1.
$v_{1}^{2} - v_{2}^{2} = 4 g r$
Substituting equation (10) in (8),
$v_{1}^{2} - g r = 4 g r$
$v_{1}^{2} = 5 g r$
$v_{1} = \sqrt{5 g r}$

Updated on:21/07/2023

|

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

PREMIERS PUBLISHERS-WORK, ENERGY AND POWER -LONG ANSWER QUESTIONS

Home
Ask Doubt
Profile