A small lamp having the form of a unfromly luminous sphere of radius is suspended at a height above the floor. The luminance o fthe lamp is equal to and is independent of direction. Find the illuminance of the floor directly below the lamp.
See the figure below. The light emitted by an element of the illuminant towards the point under consideration is
The element has the area
The disatnce
We also have
From the diagram
if we imagine a small area at then
Hence, the illuminance at is

The limit of to that value for which , for the light is emitted tangentially. Thus
.
Thus
we put
So,
Substitution gives: lux
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light33videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light60videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems92videos
MECHANICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
Similar Questions
A small lamp having the from of a unifromly sphere of radius R=6 cm is suspended at a height h=3m above the floor. The luminance of the lampis equal to L=2×104cd/m2. Find the illuminance of the floor below the lamp.
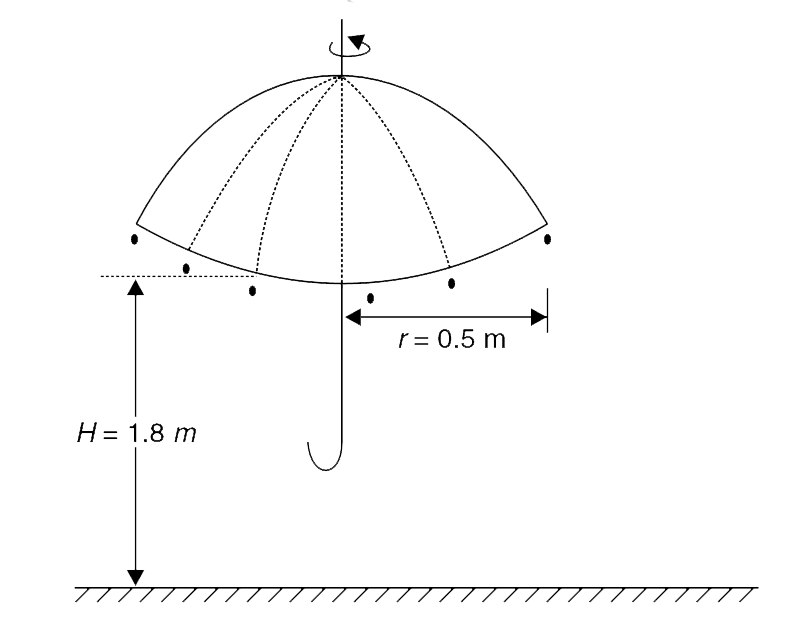
(Hint:P=∑LΔScosθ=L×πR2)View SolutionA wet umbrella is held upright (see figure). The man holding it is rotating it about its vertical shaft at an angular speed of ω=5 rad s–1. The rim of the umbrella has a radius of r=0.5 m and it is at a height of H=1.8 m from the floor. The man holding the umbrella gradually increases the angular speed to make it 2ω. Calculate the area of the floor that will get wet due to water drops spun off the rim and hitting the floor. [g=10m/s2].
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A man of 50kg mass is standing in a gravity free space at a height of 10m above the floor. He throws a stone of 0.5kg mass downwards with a speed 2m/s. When the stone reaches the floor, the distance of the man above the floor will be
A9.9mB10.1mC1.0mD20m
street lamps of 10 cm diameter and 1.8×105cdm2 luminance are suspended at a height of 12 m the distance bewteen them being 40 m Find the illuminance under each lamp and mid-way between them.
View SolutionStreet lamps of 10 cm diamter and of 1.8×105 cd/ m2 brigghtneess are suspended at a height of 12 m, the distanse between them being 40 m. Findhe illuminance under each lamp and midway between them.
View SolutionA point source is suspended at a hight h=1.0m over the centre of a round table of radius R=1.0m. The luminous intensity I of the source depends on direction so that illuminance at all points of the table is the same. Find the function I(θ), where θ is the angle between the radiation direction and the vertical, as well as the luminous flux reaching the table if I(0)=I0=100cd.
View SolutionAn illuminant shaped as a plane horizontal disc S=100cm2 in area is suspended over the centre of a round table of radius R=1.0m. Its luminance does not depend on direction and is equal illuminant be suspended to provide maximum illuminance at the circumference of the table ? How great will that illuminance be? The liuminant is assumed to be a point source.
View SolutionIf anelectric lamp be suspended at a height h from a circular table of radius r, prove that the intensity of illumination at thecentre of the table is (1+r2h2)3/2 times that at the edge of the table.
View SolutionAn object is placed in front of convex surface of a glass plano-convex lens of thickness d=9.0cm. The image of that object is formed on the plane surface of the lens serving as a screen. Find:
(a) the transverse magnification if the curvature radius of the lens's convex surface is R=2.5cm,
(b) the image illuminance if the luminance of the object i sL=7700cd/m2 and the entrance apertune diameter of the lens is D=5.0mm, losses of light are negligible.View SolutionA thin converging lens with aperture ratio D:f=1:35(D is the lens diameter, f is its focal length) provided the image of a sufficiently distance object on a photographic plate. The object luminance is L=260cd/m2. The losses of light in the lens amount to α=0.10 . Find the illuminance of the image.
View Solution

