A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O and constant angular speed . If the angular momentum of the system. calculated about O and P are denoted. by respectively, then.

and do not vary with time.
varies with time while remains constant
remains constant while varies with time
and both vary with time
The correct Answer is:C
(c ) The angular
momentum of the mass
m about O is and
is directed toward +z
direction for all
locations of m.
The angular
momentum of mass m
about P is mvl and is directed for the given location of m as shown
in the figure.
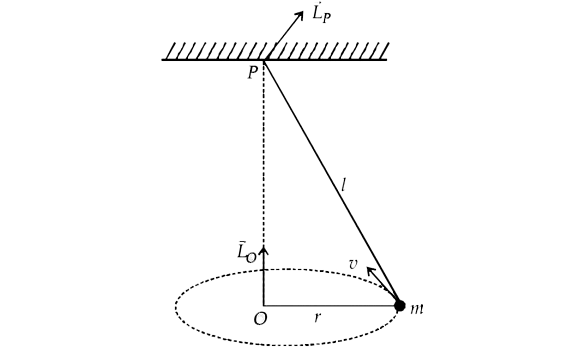
The direction of remains changing for different
locations of m.
Topper's Solved these Questions
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer1videos
ROTATIONAL MOTION
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced63videos
MOTION
- BOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced69videos
SIMPLE HARMONIC MOTION
Similar Questions
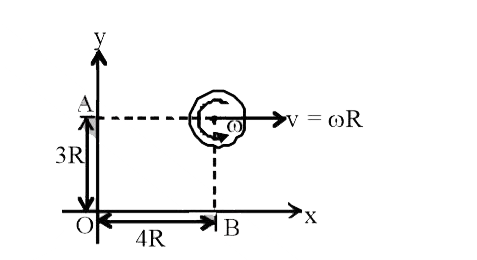
A disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
 View Solution
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View Solution
Knowledge Check
- Question 1 - Select One
A particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
 Av√a2+b2BvbCvb(a2+b2)Dva
Av√a2+b2BvbCvb(a2+b2)Dva - Question 2 - Select One
A cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
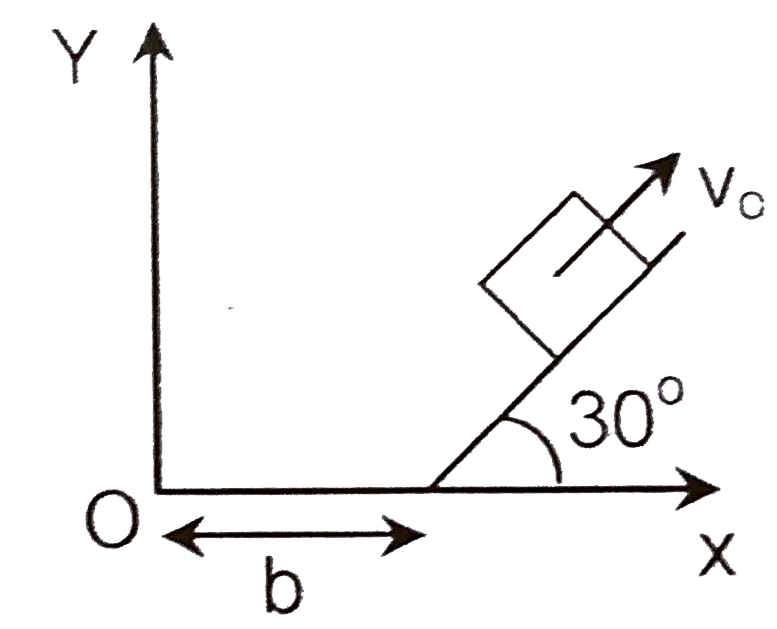 Amvob2B√3mvob2Cmvo(b−a2)DNone of these
Amvob2B√3mvob2Cmvo(b−a2)DNone of these - Question 3 - Select One or More
A mass m is attached to a rigid rod of negligible mass as shown in figure. The system is pivoted at point O and rotates about the indicated z-axis with angular velocity →ω, maintaining a fixed angle θ with the axis.
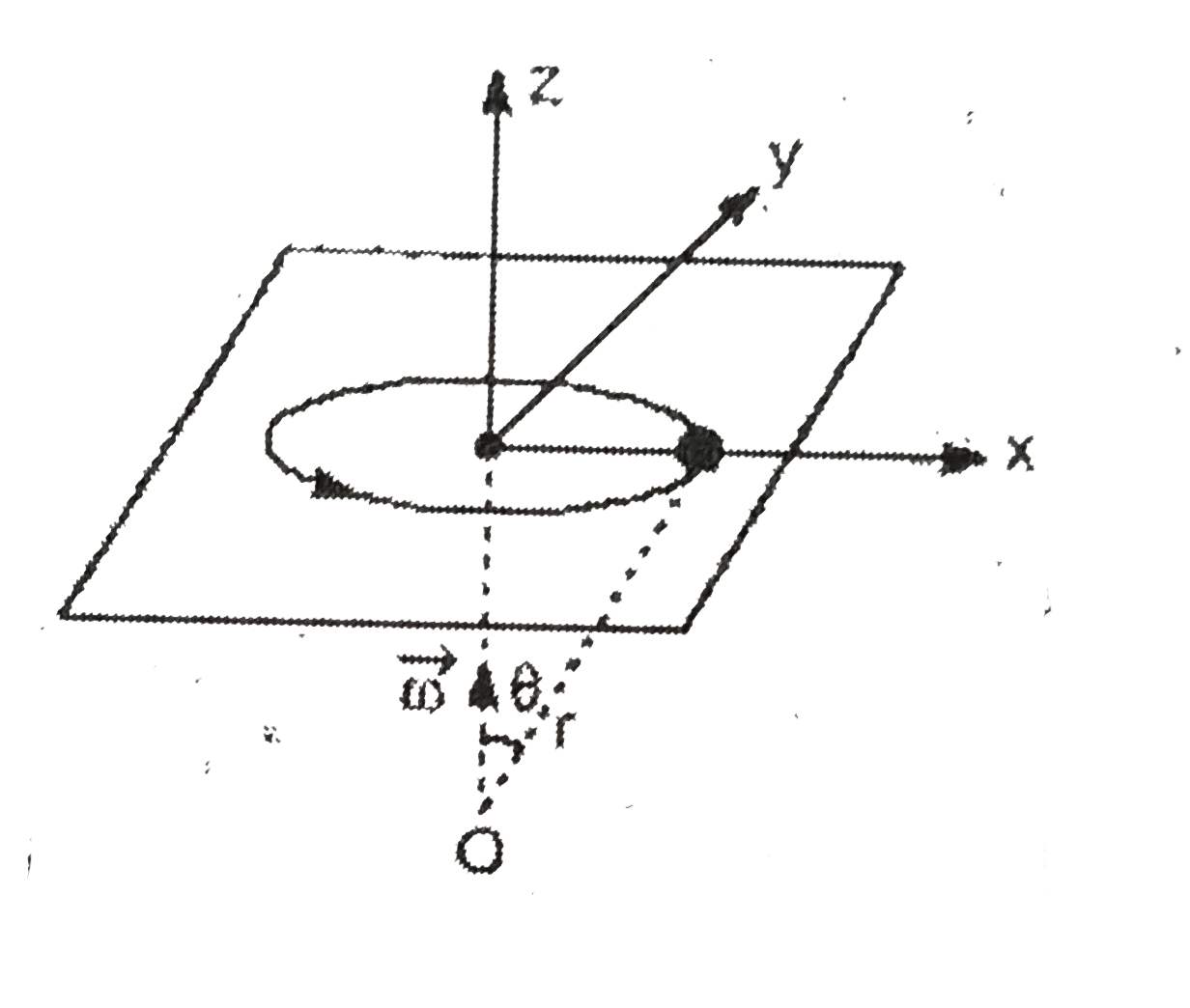 AAngular momentum →L of mass m about pivot is parallel to vector →ωBAngular momentum →L of mass m about pivot is never parallel to →ωC→L0=−mr2ωsinθcosθˆi+mr2ωsin2θˆkDAngular momentum of particle about P is parallel
AAngular momentum →L of mass m about pivot is parallel to vector →ωBAngular momentum →L of mass m about pivot is never parallel to →ωC→L0=−mr2ωsinθcosθˆi+mr2ωsin2θˆkDAngular momentum of particle about P is parallel
Two small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 View Solution
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 View Solution
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 View Solution
View Solution

