A small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
52R
52(R−r)
2510(R−r)
2710R−17r10
The correct Answer is:D
The minimum velolcity of P, topo of the loop, should be v=√g(R−r) if the sphere keeps on rolling at top v=ωR

mgh=12mv2+12Iω2+mg(2R−r)
=12mg(R−r)+12(25)mR22ω2+mg(2R−r)
=710mg(R−r)+mg(2R−r)[ωr=v=√g(R−r)]
=mg10(27R−17r)orh=110(27r−17r)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere having mass m and radius r rolls down an inclined plane. Then its kinetic energy is
View SolutionA small solid marble of mass M and radius r rolls down along the loop track, without slipping. Find the height h above the base, from where it has to start rolling down the incline such that the sphere just completes the vertical circular loop of radius R.

View Solution
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
A√34ghB√43ghC√4ghD√2ghA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
A3u24gB5u22gC7u210gDu22gA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
A√2ghB√43ghC√34ghD√4gh
A body slides down an inclined surface which ends into a vertical loop of radius R = 40cm.
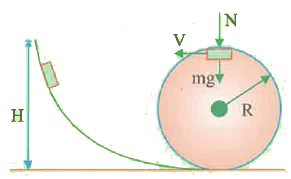
What must be the height H of the inclined surface for the body so that it does not leave contact with the surface even at the uppermost point of the loop? Assume friction to be absent.
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View SolutionA ring, a solid cylinder and sphere are rolled down on an inclined plane without slipping. Velocity of centre of mass is
View SolutionA solid sphere of mass M and radius R, rolling down a smooth inclined plane, without slipping, reaches the bottom with a velocity v. What is the height of the inclined plane in terms of the velocity v ?

View SolutionWhat is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?
View Solution
