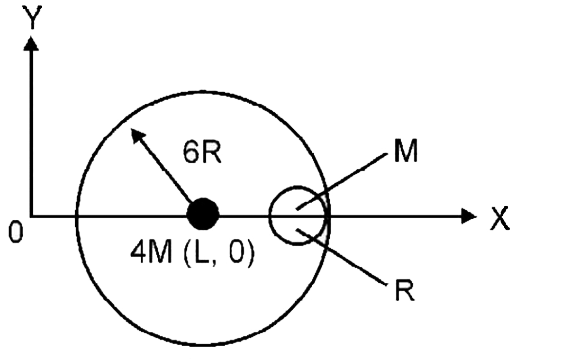
A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
The correct Answer is:B
KEY CONCEPT : The concept of centre of mass can be
applied in this problem.
When small sphere M change its position to other extreme
position, there is no external force in the horizontal direction.
Therefore the x-coordinate of c.m. will not change.
[xc.m.]∈itial=[xc.m.]f∈al
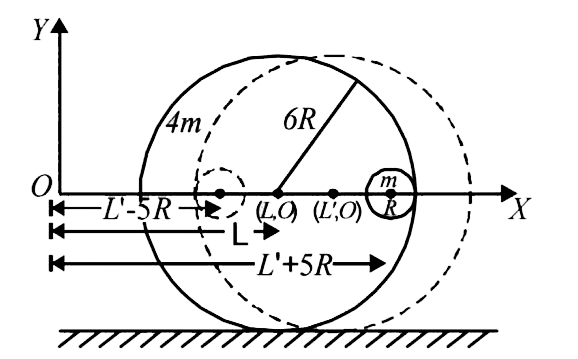
Thin line of sphere represents intial state, dotted line of
sphere represents final state.
frm(i)
(xc.m._(∈itial)=(xc.m._(f∈al)
⇒M1x1+M2x2M1+M2=M1x'1+M2x'2M1+M2
⇒(4m×L+m×5R+L4m+m=(4m×L'+m×L'−5R4m+m
⇒5L+5R=5L'−5R
⇒5L+10R=5L⇒L+2R=L'
Since, the individual center of mass of the two spheres
has a y co-rodinate zero in its initial state and its final state
therefore the y-coordinate of c.m of the two sphere system
will remain zero.
Therefore the coordinate of c.m. of bigger sphere is (L
+ 2R, 0).
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
A small sphere of radius R is held against the inner surface of α larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
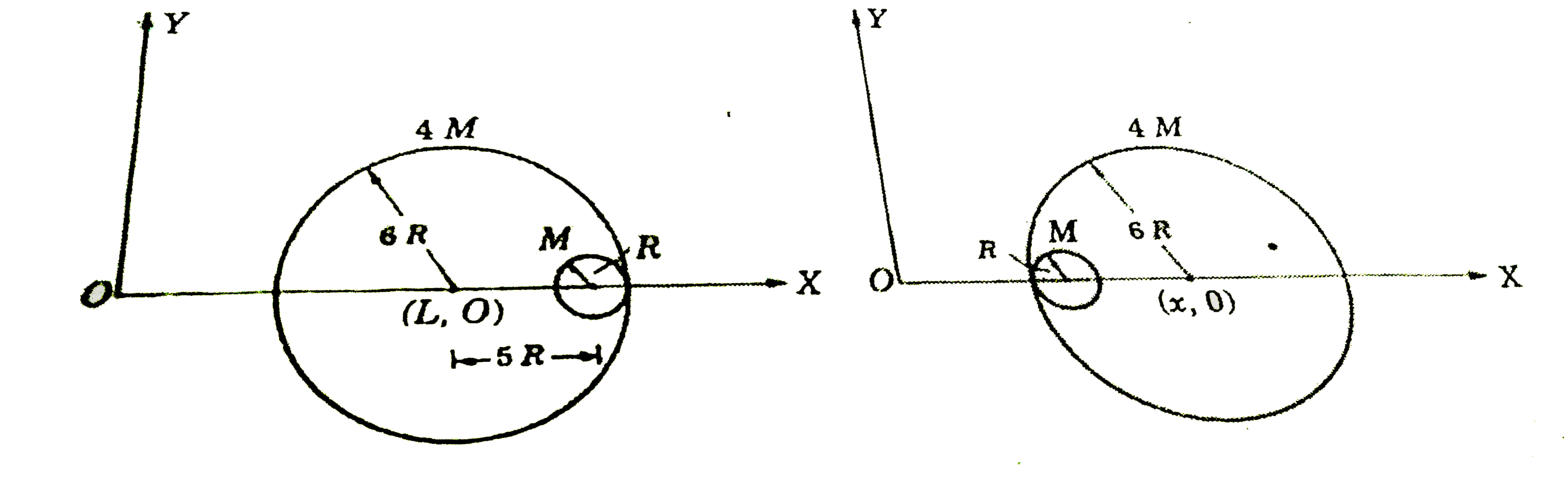
View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View Solution
Knowledge Check
A small conducting sphere of radius r is lying concentrically inside a bigger hollow conducting sphere of radius R. The bigger and smaller spheres are charged with Q and q(Q>q) and are insulated from each other. The potential difference between the spheres will be
A14πε0(qr−QR)B14πε0(QR+qr)C14πε0(qr−qR)D14πε0(qR−Qr)A solid metallic sphere of radius 6 cm is melted to form 27 equal small solid spheres. The ratio of the surface area of this sphere to that of a small sphere is
A3:1B9:1C1:9D1:3A solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres . The ratio of the surface area of this sphere to that of a small sphere is
A4:1B1:16C16:1D1:4
A sphere of mass M and radius R is held on the inner wall of a hollow sphere of mass 4M and radius 6R .The bigger sphere is kept on a smooth horizontal table and the centres of the two spheres lie on horizontal line.The system of two spheres is released from this position. The smaller sphere slides on the inner smooth wall to reach the other extreme position (shown in dotted line).The displacement of the centre of the larger sphere as the smaller sphere moves from one extreme to another is xcm. Value of x is: ( Take R=4.5cm) qquad y qquad yR Delta M
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA sphere of radius 6 cm is melted and made three small spheres of radius 3 cm, 4 cm and r cm respectively, the value of r is ....................
View SolutionA solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres. The ratio of the surface area of this sphere to that of a small sphere is
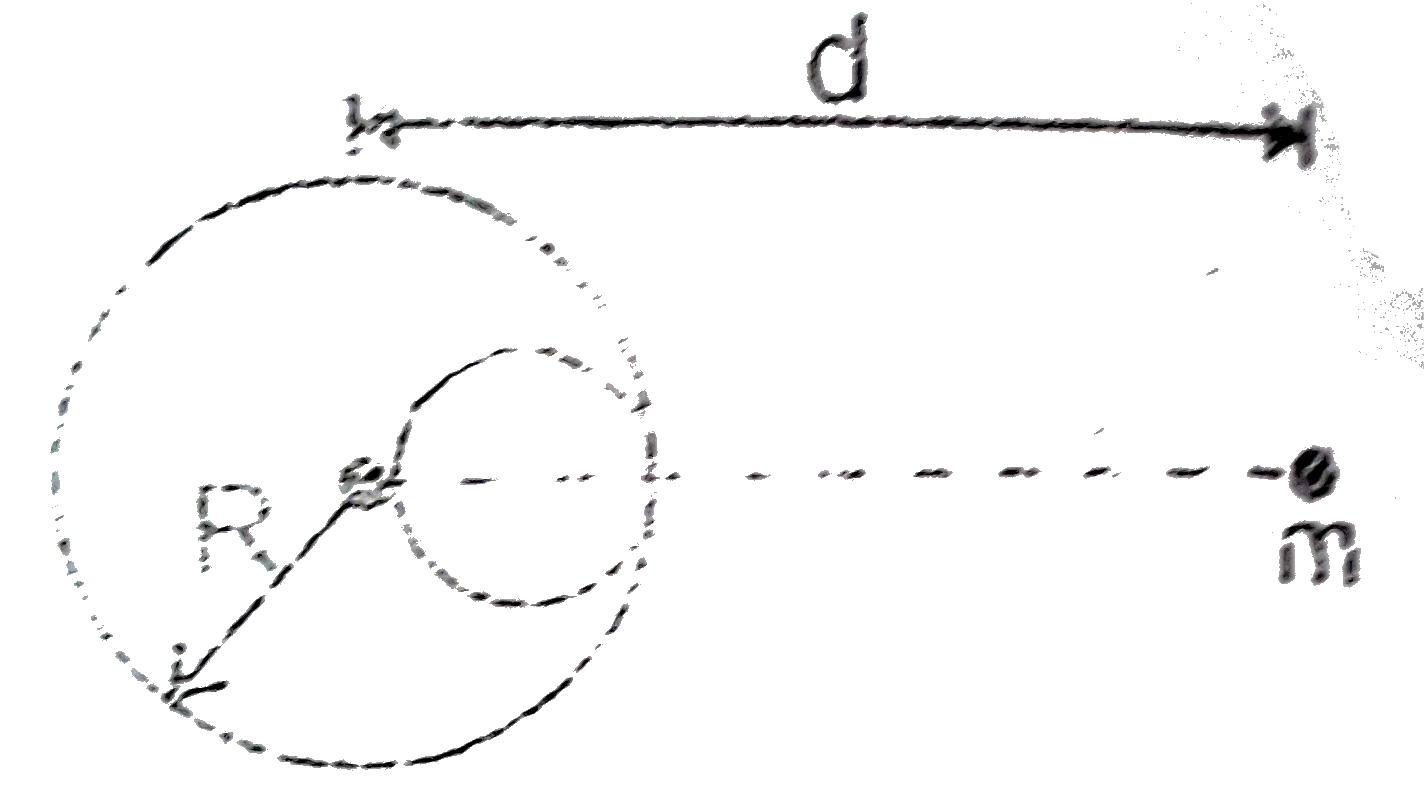
View SolutionA spherical hollow cavity is made in a lead sphere of radius R such that is surface touches the outside surface of the lead sphere and passes through its centre. The mass of the sphere before hollowing was M with what gravitational force will the hollowed out lead sphere attract a small sphere of mass m which lies at a distacne d from the centre of the lead sphere on the straight line connecting the centeres of the spheres and that of the hollow if d=2R
 .
.
View Solution
