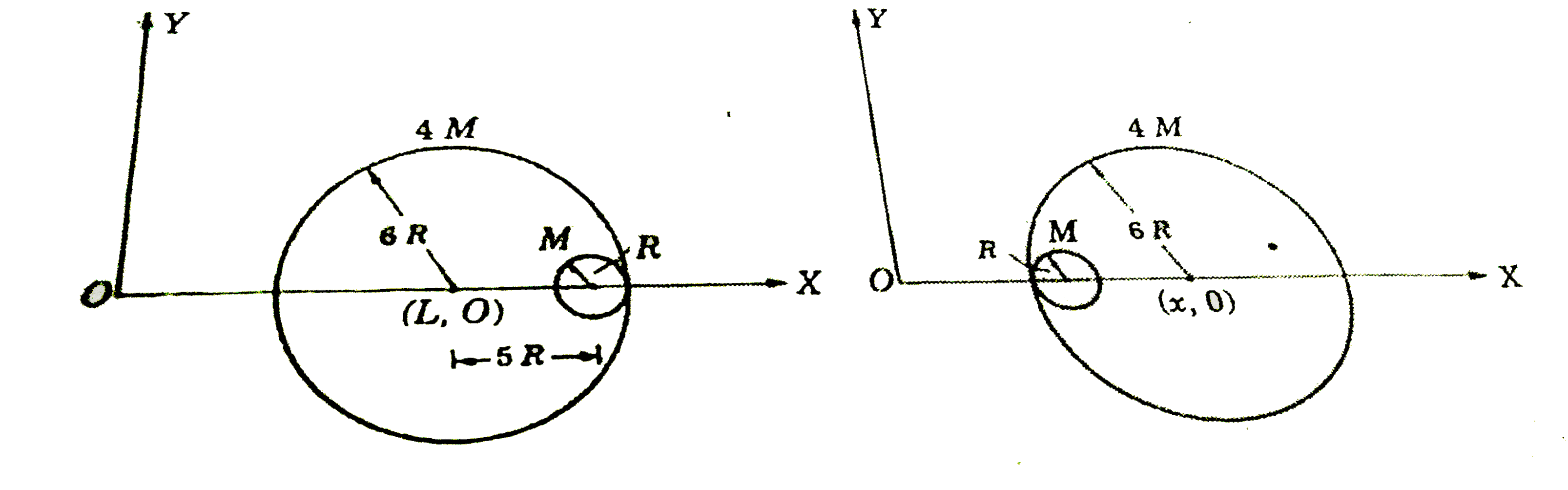
A small sphere of radius R is held against the inner surface of larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
Step by step video solution for A small sphere of radius R is held against the inner surface of alpha larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
Similar Questions
A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
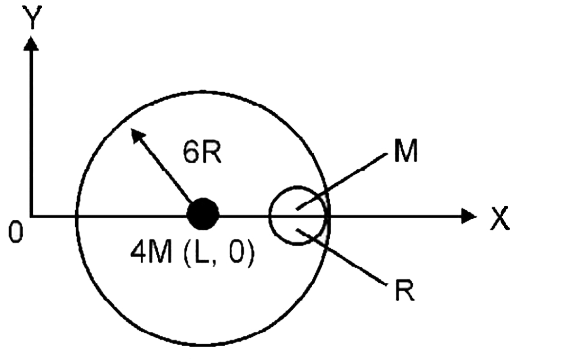
View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View Solution
Knowledge Check
A small conducting sphere of radius r is lying concentrically inside a bigger hollow conducting sphere of radius R. The bigger and smaller spheres are charged with Q and q(Q>q) and are insulated from each other. The potential difference between the spheres will be
A14πε0(qr−QR)B14πε0(QR+qr)C14πε0(qr−qR)D14πε0(qR−Qr)A solid metallic sphere of radius 6 cm is melted to form 27 equal small solid spheres. The ratio of the surface area of this sphere to that of a small sphere is
A3:1B9:1C1:9D1:3A solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres. The ratio of the surface area of this sphere to that of a small sphere is
A4:1B1:16C16:1D1:4
A sphere of mass M and radius R is held on the inner wall of a hollow sphere of mass 4M and radius 6R .The bigger sphere is kept on a smooth horizontal table and the centres of the two spheres lie on horizontal line.The system of two spheres is released from this position. The smaller sphere slides on the inner smooth wall to reach the other extreme position (shown in dotted line).The displacement of the centre of the larger sphere as the smaller sphere moves from one extreme to another is xcm. Value of x is: ( Take R=4.5cm) qquad y qquad yR Delta M
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionThree identical spheres each of radius 'R' are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is.
View SolutionA small box of mass m is placed on the outer surface of a smooth fixed sphere of radius R at a point where the radius makes a angle Pse with the vertical. The box is released from this position. Find the distance travelled by the box before it leaves contact with the sphere.
View SolutionA solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres . The ratio of the surface area of this sphere to that of a small sphere is
View Solution
