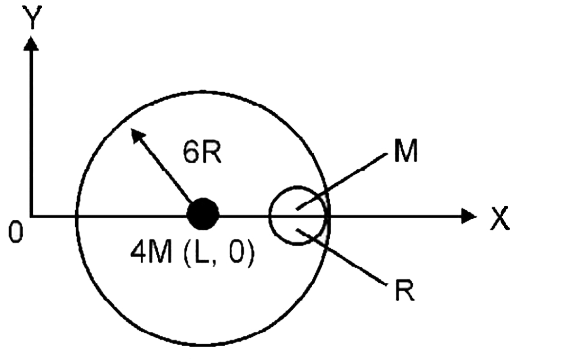
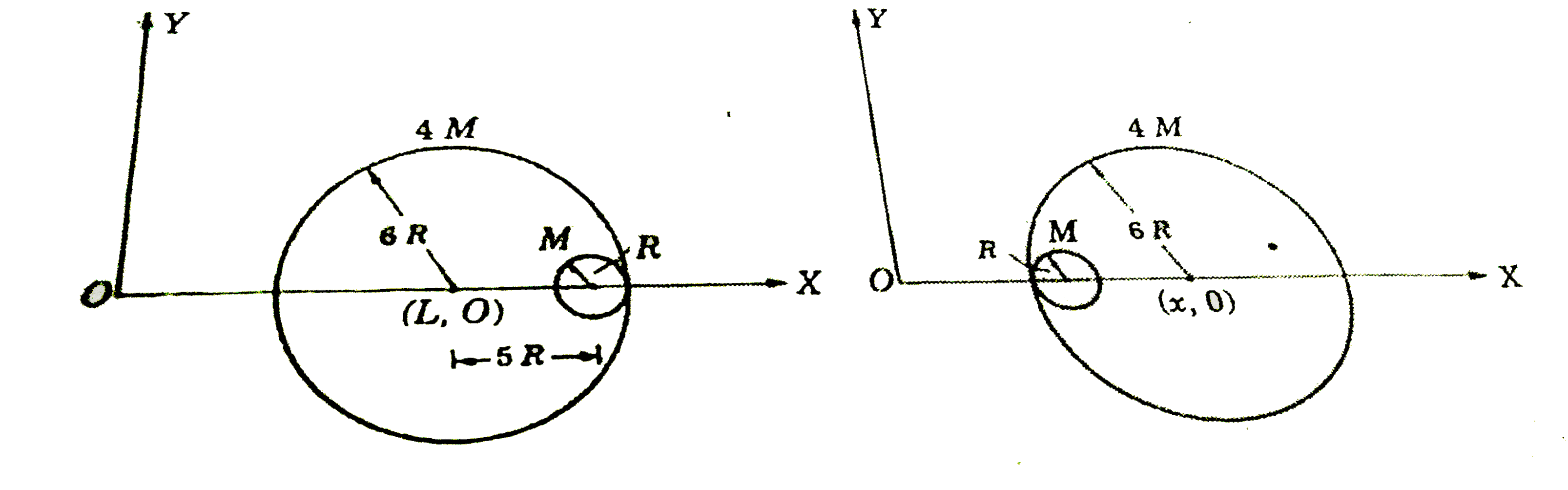
A small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

Step by step video & image solution for A small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Example50videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - Level 1110videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type13videos
FORCE ANALYSIS
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN12videos
RIGID BODY MOTION
Similar Questions
A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
 View Solution
View SolutionA small sphere of radius R is held against the inner surface of α larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20 - Question 2 - Select One or More
A small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
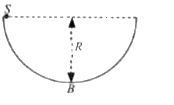 AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2
AThe fraction of translational kinetic energy at the sphere is 5/7.BThe fraction of rotational kinetic energy of the sphere is 2/7.CThe fraction of rotational kinetic energy of the sphere is 27mv2.DThe total kinetic energy of the sphere at the bottom of the bowl is 27mv2 - Question 3 - Select One or More
A solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)
 AWork done by force F when the centre of mass move a distance S is 2 FSBspeed of the CM when CM moves a distance S is √207FSMCwork done by the Force F when CM move a distance S is FSDspeed of the CM when CM moves a distance S is √65FSM
AWork done by force F when the centre of mass move a distance S is 2 FSBspeed of the CM when CM moves a distance S is √207FSMCwork done by the Force F when CM move a distance S is FSDspeed of the CM when CM moves a distance S is √65FSM
A sphere of mass M and radius R is held on the inner wall of a hollow sphere of mass 4M and radius 6R .The bigger sphere is kept on a smooth horizontal table and the centres of the two spheres lie on horizontal line.The system of two spheres is released from this position. The smaller sphere slides on the inner smooth wall to reach the other extreme position (shown in dotted line).The displacement of the centre of the larger sphere as the smaller sphere moves from one extreme to another is xcm. Value of x is: ( Take R=4.5cm) qquad y qquad yR Delta M
View SolutionThree identical spheres each of radius 'R' are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is.
View SolutionA solid metallic sphere of radius 6 cm is melted to form 27 equal small solid spheres. The ratio of the surface area of this sphere to that of a small sphere is
View SolutionA solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres. The ratio of the surface area of this sphere to that of a small sphere is
View SolutionA solid metallic sphere of radius 8 cm is melted to form 64 equal small solid spheres . The ratio of the surface area of this sphere to that of a small sphere is
View Solution

