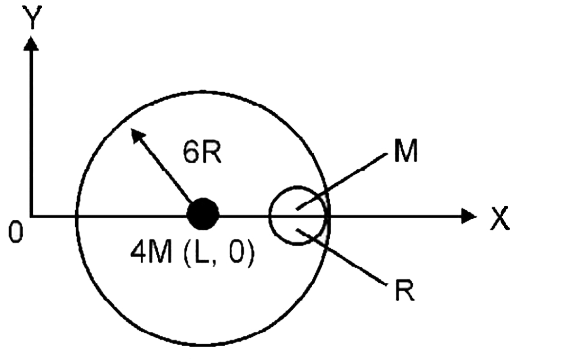
A small sphere of radius R is kept attached to the smooth inner wall of a hollow sphere of radius 6 R Fig. The system is kept on a frictionless horizontal table. On releasing the small sphere, as it reaches the other end of the diameter, what will be the coordinates of the centre of the large sphere? Masses of the small and large sphere are M and 4M respectively.
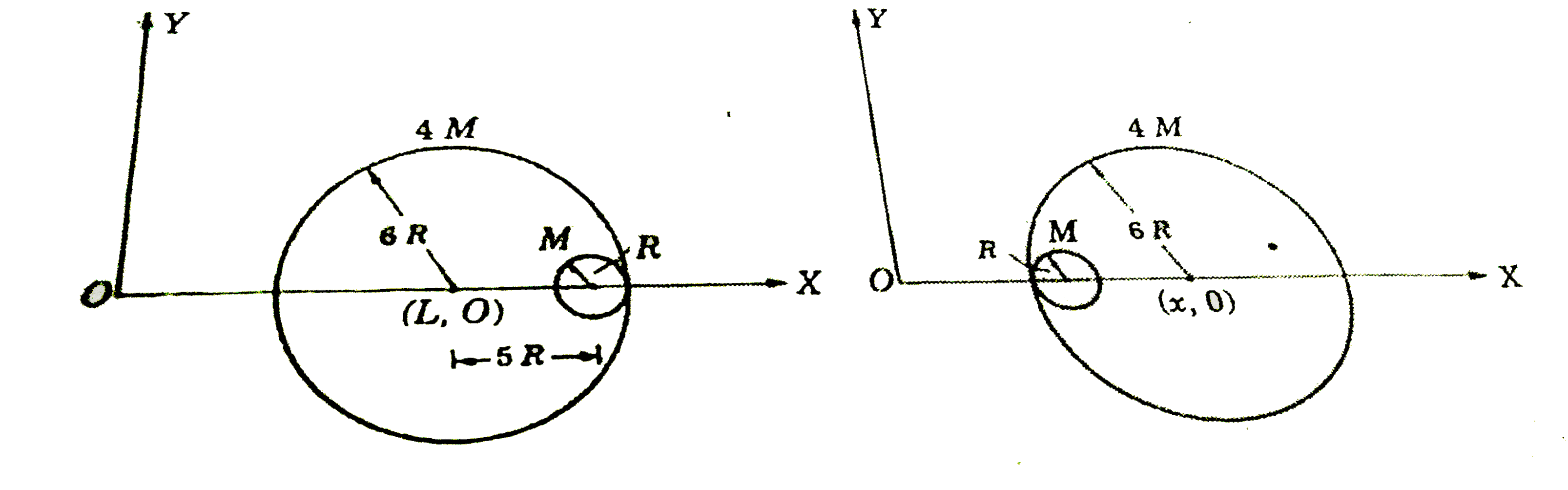
As shown in Fig the coordinates of the centre of the large sphere is (L,0). Hence, coordinates of the centre of the small sphere is ( L+6R-R,0) or (L+5R,0). So, if (xcm) are the coordinates of the centre of mass, then,
xcm=m1x1+m2x2m1+m2
=4ML+M(L+5R)5M=5M(L+R)5M=L+R
The coordinates of the centre of mass remain unchanged in the absence of any external force.
Let the coordinates of the centre of the large sphere be (a,0) when the small sphere reaches the opposite end A. The coordinates of the centre of the small sphere become (a-5R,0). As the position coordinates of the centre of mass remain unchanged,
L+R=4Ma+M(a−5R)4M+M=5Ma−5MR5M=a−R
∴ a=L+R+R=L+2R
Hence, the new coordinates of the centre of the large sphere will be (L+2R,0).

Topper's Solved these Questions
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - HIGHER ORDER THINKING SKILL (HOTS) QUESTIONS
18 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - EXERCISE (Multiple Choice Questions )
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - CBSE SCANNER
16 Videos
- SUPERPOSITION OF WAVESBOOK - CHHAYA PUBLICATIONCHAPTER - SUPERPOSITION OF WAVESEXERCISE - CBSE Scanner
14 Videos
Similar Questions
A small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The mass of large and small spheres are 4M and M respectively. This arrangement is placed on a horizontal table. There is no friction between any surface of contact. The small sphere is now released. The x coordinate of the centre of the larger sphere when the smaller sphere reaches the other extreme position, is found to be (L+nR) , find n.
View SolutionA small sphere of radius R is held against the inner surface of a larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively , this arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
View SolutionA sphere of mass M and radius R is held on the inner wall of a hollow sphere of mass 4M and radius 6R .The bigger sphere is kept on a smooth horizontal table and the centres of the two spheres lie on horizontal line.The system of two spheres is released from this position. The smaller sphere slides on the inner smooth wall to reach the other extreme position (shown in dotted line).The displacement of the centre of the larger sphere as the smaller sphere moves from one extreme to another is xcm. Value of x is: ( Take R=4.5cm) qquad y qquad yR Delta M
View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View SolutionA small sphere of radius R is held against the inner surface of larger sphere of radius 6R (as shown in figure). The masses of large and small spheres are 4M and M respectivley. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the coordinates of the centre of the large spheres, when the smaller sphere reaches the other extreme position.

View SolutionA small sphere of radius R is held against the inner surface of α larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
View SolutionA large solid sphere of diameter 15m is melted and recast into several small spheres of diameter 3m. What is the percentage increase in the surface area of the smaller spheres over that of the large sphere?
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View Solution
