Question

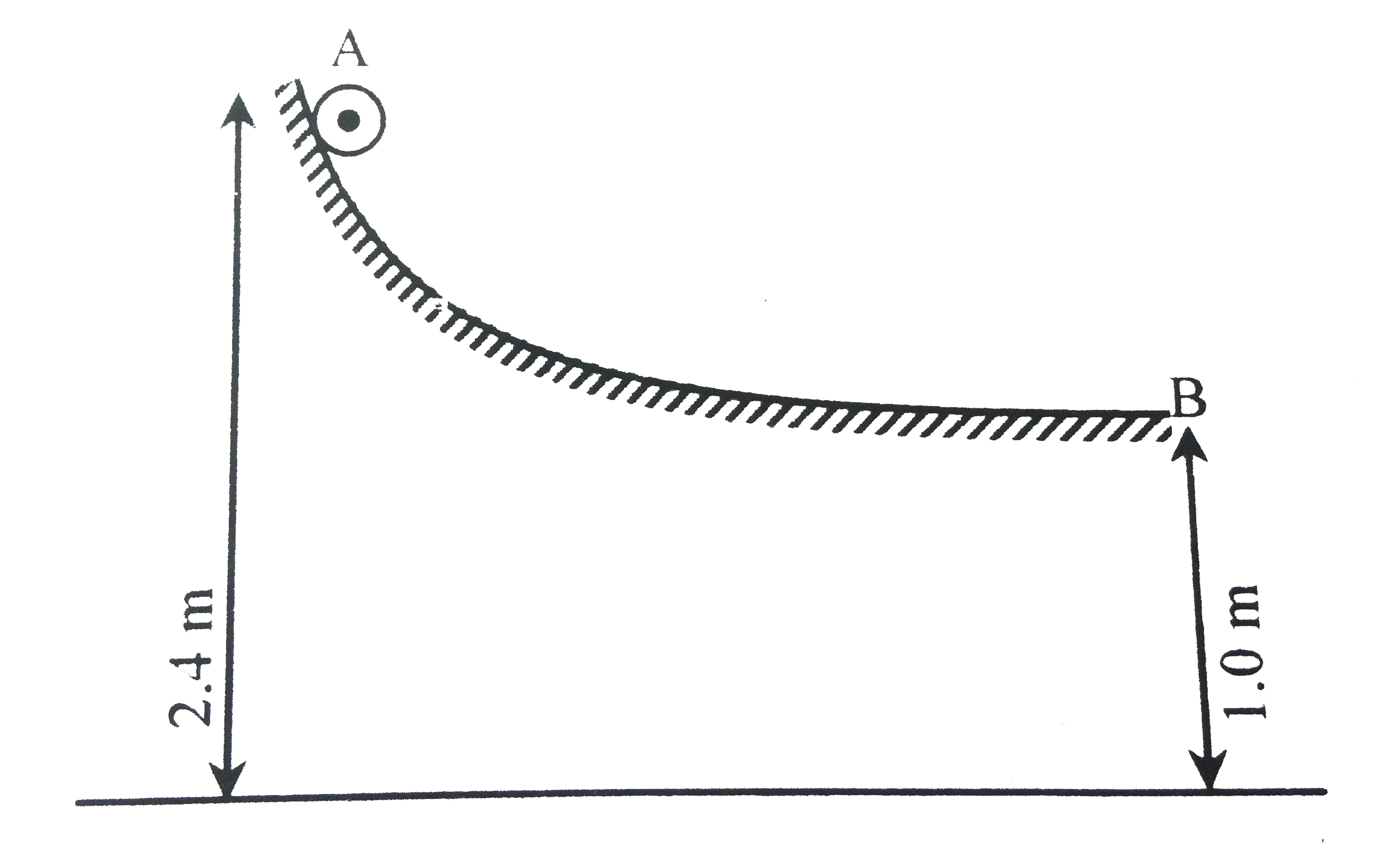
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground lenvel and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown i fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? Explain.

Answer

B

Explanation

KEY CONCEPT : Applying law of conservation of energy
at point D and Point A
`P.E. at D = P.E. at Q + (K.E)_T + (K.E.)_R where` (K.E)_T = Translational K.E and (K.E)_R = Rotational K.E.
`rArr mg)2.4) mg(1) + (1) + (1)/(2)mv^2 +(1)/(2) I omega^2 ....(i)`
Since the case is of rolling without slipping
`:. v = romega`
`:. omega = (v)/(r )` where r is the radius of the sphere

Also, `I= (2)/(5)mr^2`
Putting in equation (i)
`mg(2.4 - 1) = (1)/(2)mv^2 +(1)/(2) ((2)/(5) mr^2)) (v^2)/(r^2)`
or, ` gxx1.4 = (7v^2)/(10) rArr v = 4.43 m/s`
After point Q, the body takes a parablic path,
The vertical motion perameters of parabolic motion will be
`u_y = 0 S_y = 1m`
`a_y = 9.8m/s^2 1 = 4.9t_y^2`
`t_y =(1)/(sqrt(4.9) = 0.45 sec`
Applying this time in horizontal motion of parabolic paht,
BC = 4.43xx0.45 = 2m