A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.
![A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as rho(L)=rho(0)[4-(3h//h(0))].The density of the ball is (5//2)rho(0). The height of the vessel is h(0)=12//pi^(2) Consider r lt lt h(0) and g = 10 m//s^(2). Where will the ball come in the equilibrium?](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_C04_E01_185_Q01.png)
Where will the ball come in the equilibrium?
At a depth h0/2 from top
At the bottom of the vessel
At a depth 3h0/4 from top
The ball will never be at equilirbium
The correct Answer is:A
Let the net force on this particle be zero at height h. Then weight
= upthrust (at h)
⇒43πr3g52ρ0−43πr2gρ0[4−3hh0]
⇒3hh0=4−52=32⇒h=h02………..i
Therefore, at h=h02, the equilibrium position, the particle has a speed in downward direction due to which it will move downward. Let at a further depth x from h02.
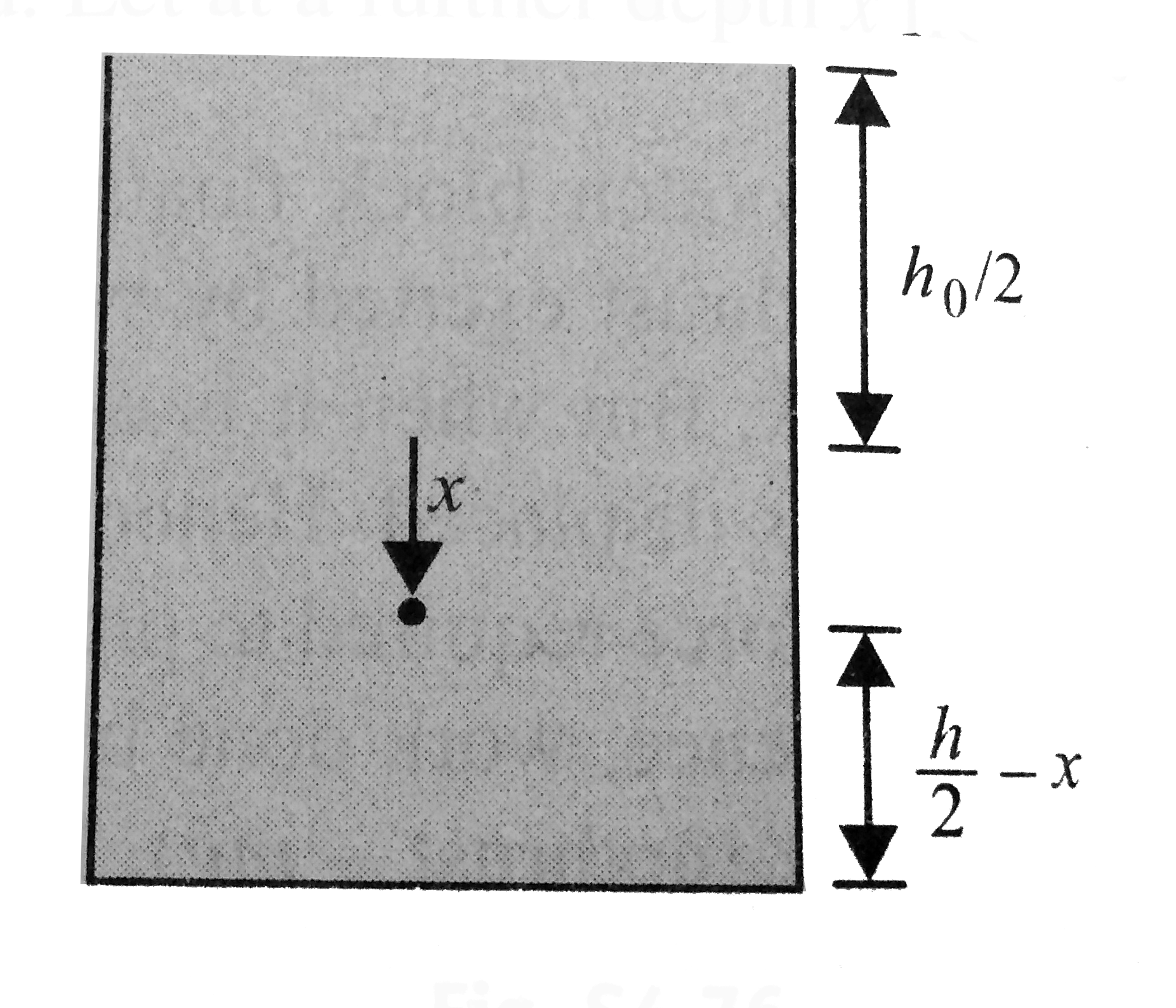
Fnet= upthrust − weight
=43πr3gρ0⎡⎢
⎢⎣4−3(h02−x)h0⎤⎥
⎥⎦−43πr3g52ρ0
=43πr3ρ0g[4−32+3xh0−52]=4πr3ρ0gh0x
∴F=4πr3ρ0gh0x
Since the net force on the and displacement of ball from its mean position are oppositely directed the particle executes SHM about its mean position i.e. h=h02
∴F=ma=−4πr3ρ0gh0x
=43πr352ρ0a=−4πr3ρ0gh0x
⇒a=−6g5h0x=−(12h0)x=−ω2x
where ω=√12h0=s√1212πr2=π
Hence, time taken by the particle to reach the bottom is
t=T2=122πω=πω=ππ=1s
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Linked Comprehension
43 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
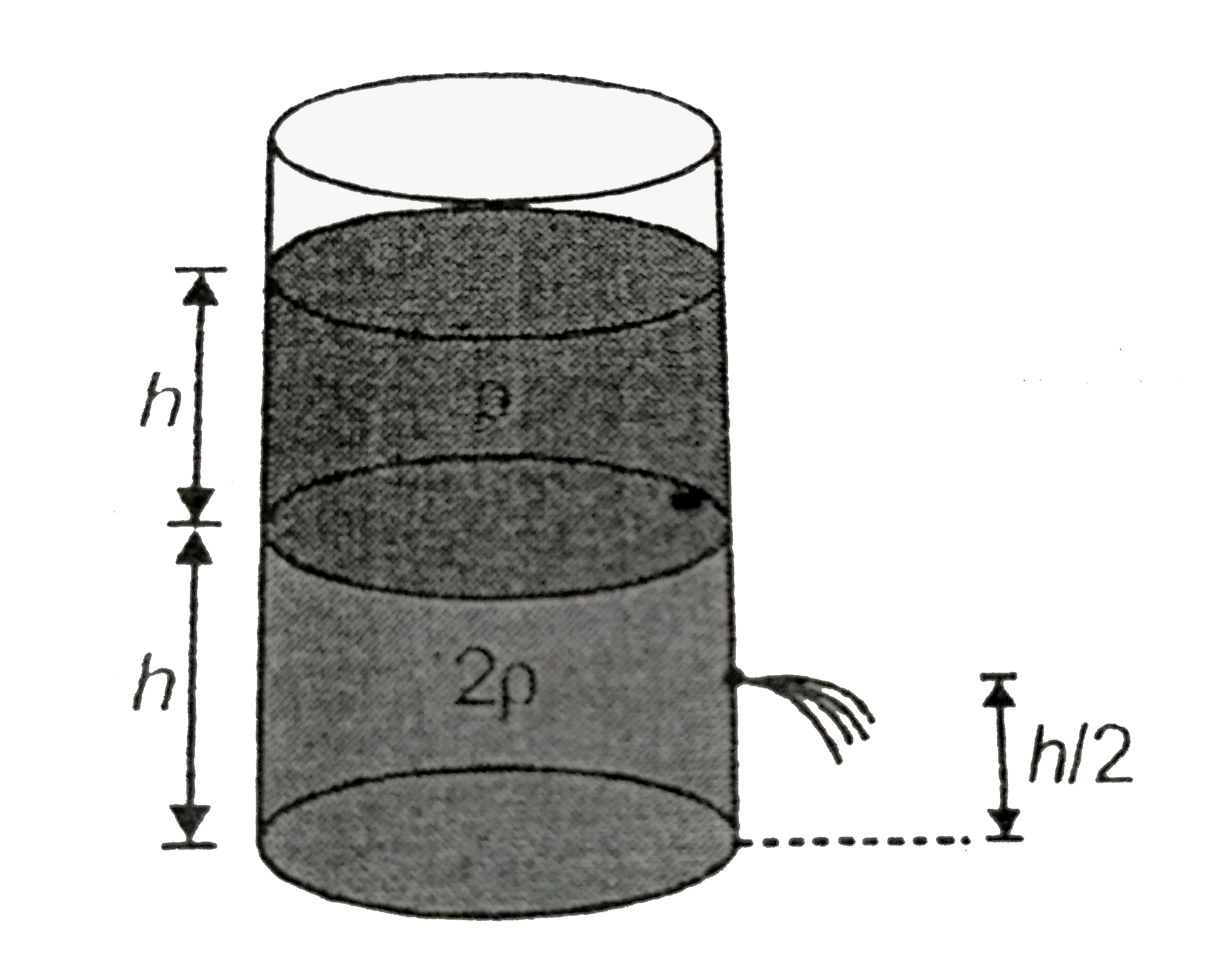
A vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is
View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View Solution
Knowledge Check
A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The ball will reach at the bottom of the vesselAin 1sBin 2sCin 0.5sDthe ball will not reach at the bottom of the vesselA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The motion of the ball in the vessel isAoscillatory but not simple harmonic motionBsimple harmonic motion with time period 2sCsimple harmonic motion with time period 1sDthe motion is not oscillatoryA uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
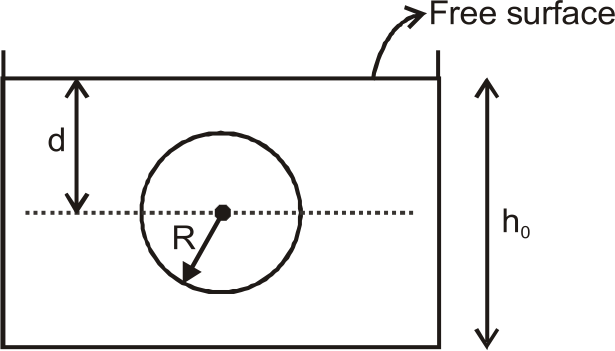 Aσ=ρ0(1+d2h0)Bσ=ρ0(1−d2h0)Cσ=ρ0(1+2dh0)Dσ=ρ0(1+dh0)
Aσ=ρ0(1+d2h0)Bσ=ρ0(1−d2h0)Cσ=ρ0(1+2dh0)Dσ=ρ0(1+dh0)
A spherical region of space has a distribution of charge such that the volume charge density varies with the radial distance from the centre r as ρ=ρ0r3,0≤r≤R where ρ0 is a positive constant. The total charge Q on sphere is
View SolutionA sperical ball of radius r and relative density 0.5 is floating in equilibrium in water with half of it immersed in water. The work done in pushing the ball down so that whole of it is just immersed in water is [ρ is the density of water]-
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
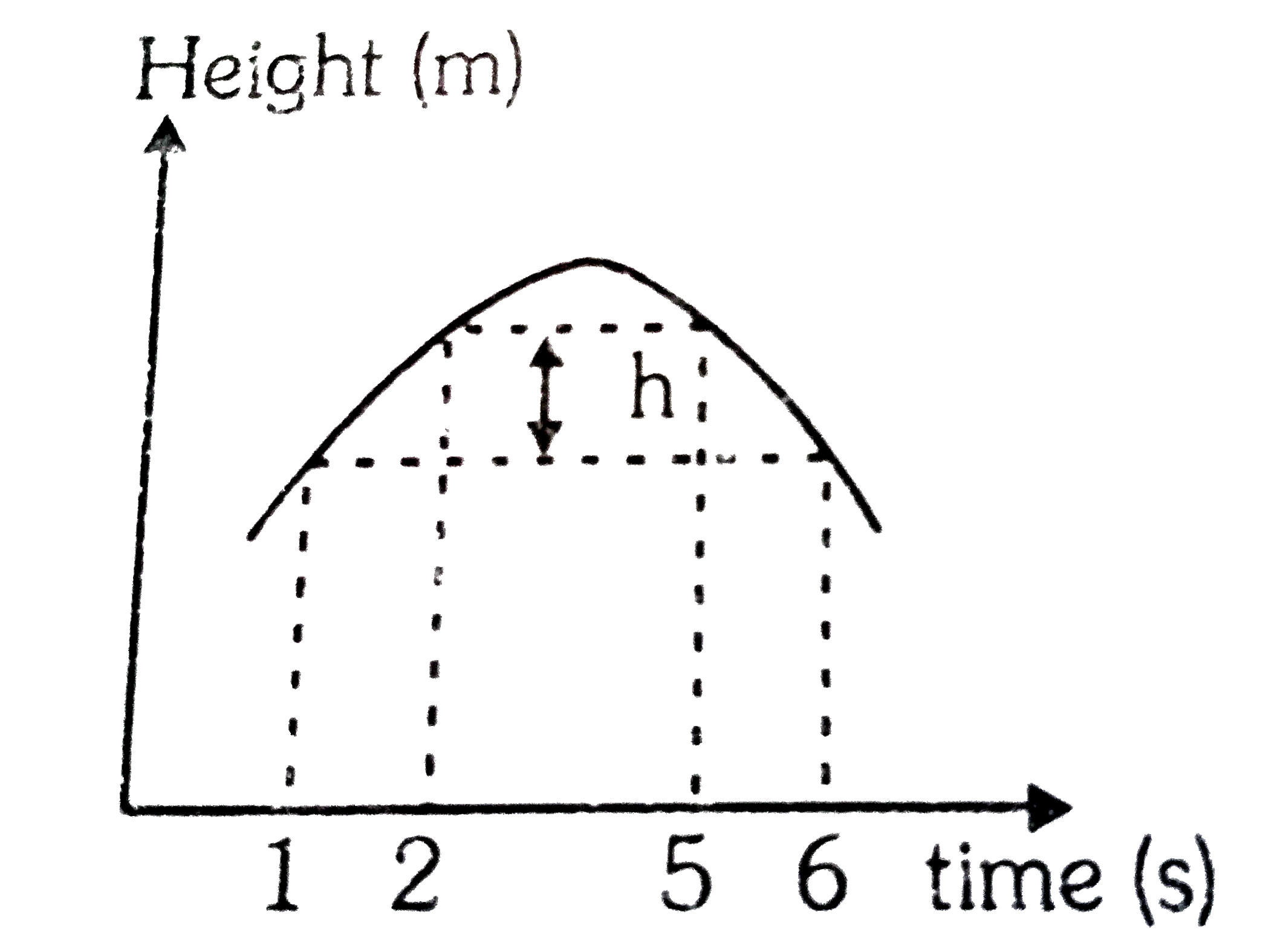
View SolutionA small ball of density 4ρ0 is released from rest just below the surface of a liquid. The density of liquid increases with depth as ρ=ρ0(1+ay) where a=2m−1 is a constant. Find the time period of its oscillation. (Neglect the viscosity effects).
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View Solution
