A small spherical ball of radius is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height (measured from the bottom) as .The density of the ball is (. The height of the vessel is Consider and .
![A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as rho(L)=rho(0)[4-(3h//h(0))].The density of the ball is (5//2)rho(0). The height of the vessel is h(0)=12//pi^(2) Consider r lt lt h(0) and g = 10 m//s^(2). The motion of the ball in the vessel is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_VOL2_C04_E01_186_Q01.png)
The motion of the ball in the vessel is
oscillatory but not simple harmonic motion
simple harmonic motion with time period
simple harmonic motion with time period
the motion is not oscillatory
The correct Answer is:B
Let the net force on this particle be zero at height . Then weight
upthrust (at )
………..i
Therefore, at , the equilibrium position, the particle has a speed in downward direction due to which it will move downward. Let at a further depth from .

upthrust weight
Since the net force on the and displacement of ball from its mean position are oppositely directed the particle executes about its mean position i.e.
where
Hence, time taken by the particle to reach the bottom is
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is

View SolutionA ball of radius R is uniformly charged with the volume density ρ. Find the flux if the electric field strength vector across the balls section formed by the plane located at a distance r0<R from the centre of the ball.
View Solution
Knowledge Check
A small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

The ball will reach at the bottom of the vesselAin 1sBin 2sCin 0.5sDthe ball will not reach at the bottom of the vesselA small spherical ball of radius r is released from its completely submerged Position (as shown in the figure) in a liquid whose density varies with height h (measured from the bottom) as ρL=ρ0[4−(3h/h0)].The density of the ball is (5/2)ρ0. The height of the vessel is h0=12/π2 Consider r<<h0 and g=10m/s2.

Where will the ball come in the equilibrium?AAt a depth h0/2 from topBAt the bottom of the vesselCAt a depth 3h0/4 from topDThe ball will never be at equilirbiumA uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
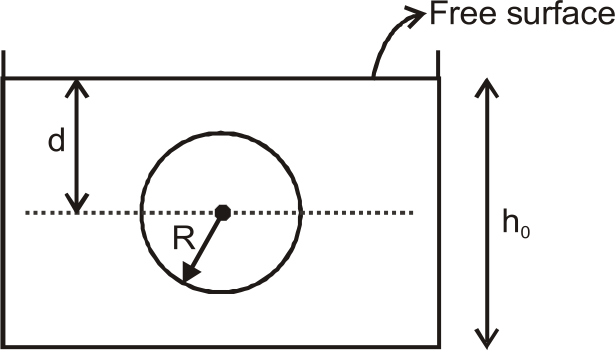 Aσ=ρ0(1+d2h0)Bσ=ρ0(1−d2h0)Cσ=ρ0(1+2dh0)Dσ=ρ0(1+dh0)
Aσ=ρ0(1+d2h0)Bσ=ρ0(1−d2h0)Cσ=ρ0(1+2dh0)Dσ=ρ0(1+dh0)
A spherical region of space has a distribution of charge such that the volume charge density varies with the radial distance from the centre r as ρ=ρ0r3,0≤r≤R where ρ0 is a positive constant. The total charge Q on sphere is
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
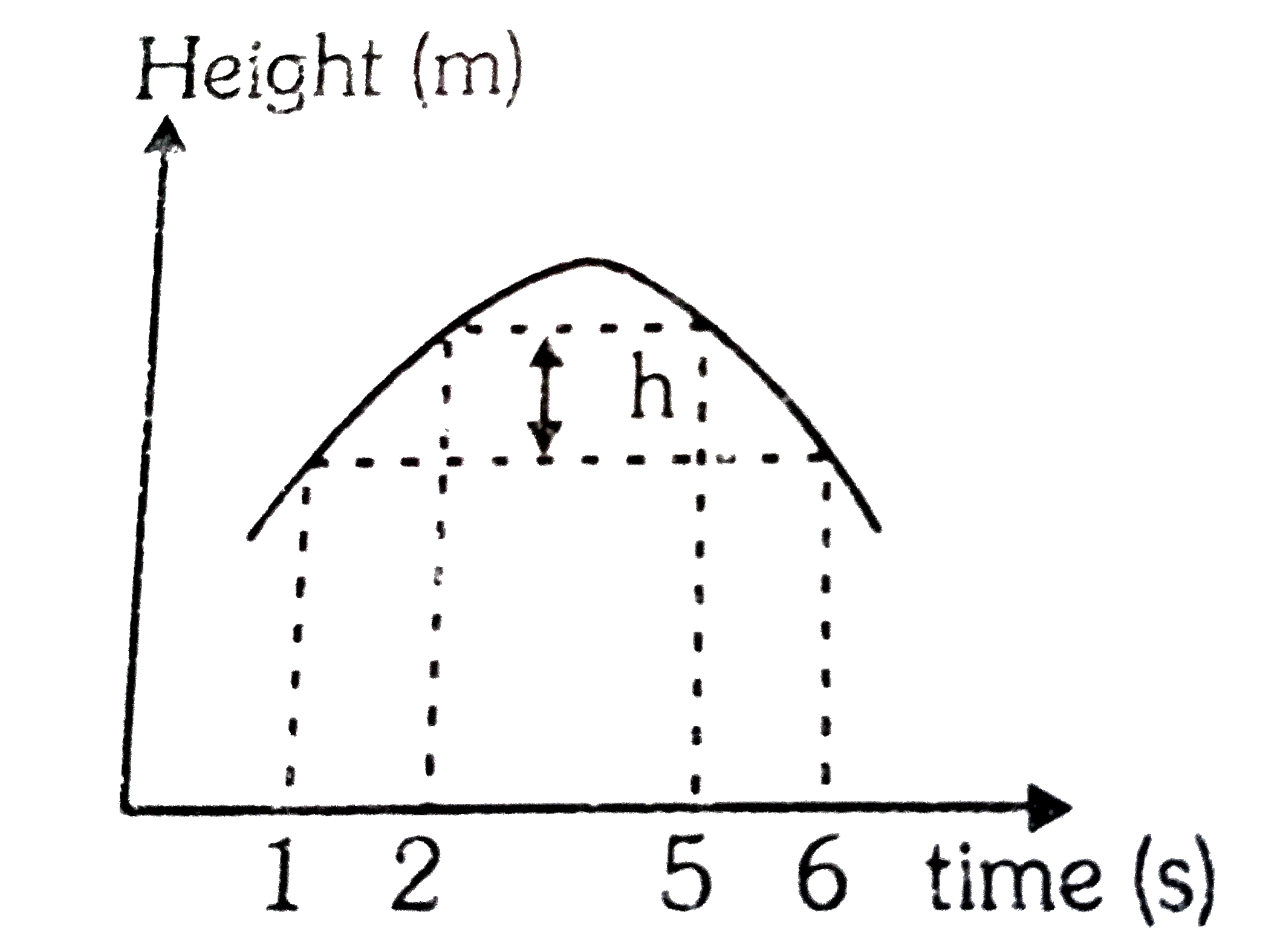
View SolutionA small ball of density 4ρ0 is released from rest just below the surface of a liquid. The density of liquid increases with depth as ρ=ρ0(1+ay) where a=2m−1 is a constant. Find the time period of its oscillation. (Neglect the viscosity effects).
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View Solution
