A small spherical monoatomic ideal gas bubble $(γ = 5 / 3)$ is trapped inside a liquid of density $ρ$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is $T_{0}$ , the height of the liquid is H and the atmospheric pressure $P_{0}$ (Neglect surface tension).

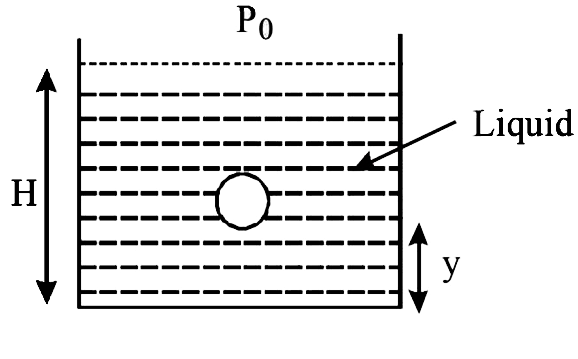
When the gas bubble is at a height y from the bottom, its temperature is-

$p_{1} n R g T_{0} \frac{(P_{0} + p_{1} g H)}{{(P_{0} + p_{1} g y)}_{0}^{\frac{7}{2}}}$

$\frac{p_{1} n R g T_{0}}{{(P_{0} + p_{1} g H)}_{0}^{\frac{2}{5}} (P_{0} + p_{1} {g (H - y)}^{\frac{3}{5}})}$

$p_{1} n R g T_{0} \frac{{(P_{0} + p_{1} g H)}_{0}^{3 - 5}}{{(P_{0} + p_{1} g y)}_{0}^{\frac{8}{5}}}$

$\frac{p_{1} n R g T_{0}}{{(P_{0} + p_{1} p_{1} g H)}_{0}^{\frac{2}{5}} [P_{0} + p_{1} {g (H - y)}^{\frac{3}{5}})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

For ideal gas we can write
PV=nRT
Substituting appropriate values for the point at a height y from the bottom we can write the following :
$V = \frac{n R T}{P} = \frac{\frac{n R T_{0} {[P_{0} + p_{1} g (H - y)]}_{0}^{\frac{2}{6}}}{{[P_{0} + p_{1} g H]}_{0}^{\frac{2}{5}}}}{[P_{0} + p_{1} g (H - y)]}$
$V = \frac{n R T_{0}}{{[P_{0} + p_{1} g H]}_{0}^{\frac{2}{5}} {[P_{0} + p_{1} g (H - y)]}_{0}^{\frac{3}{5}}}$

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Knowledge Check

A small spherical monoatomic ideal gas bubble $(γ = \frac{5}{3})$ is trapped inside a liquid of density $ρ_{l}$ (see figure) . Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is $T_{0}$ , the height of the liquid is H and the atmospheric pressure is $P_{0}$ (Neglect surface tension).

When the gas bubble is at a height y from the bottom , its temperature is :-
A $T_{0} {(\frac{P_{0} + ρ_{l} g H}{P_{0} + ρ_{l} g y})}^{2 / 5}$
B $T_{0} {(\frac{P_{0} + ρ_{l} g (H - y)}{P_{0} + ρ_{l} g H})}^{2 / 5}$
C $T_{0} {(\frac{P_{0} + ρ_{l} g H}{P_{0} + ρ_{l} g y})}^{3 / 5}$
D $T_{0} {(\frac{P_{0} + ρ_{l} g (H - y)}{P_{0} + ρ_{l} g H})}^{3 / 5}$
A small spherical monoatomic ideal gas bubble $(γ = 5 / 3)$ is trapped inside a liquid of density $ρ$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is $T_{0}$ , the height of the liquid is H and the atmospheric pressure $P_{0}$ (Neglect surface tension).

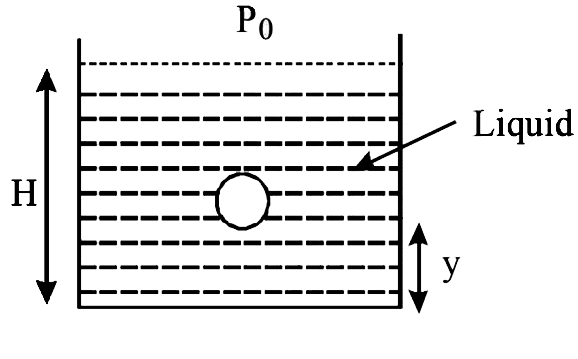
The buyoncy force acting on the gas bubble is (Assume R is the universal gas constant)
A $ρ_{l} n R g T_{0} \frac{{(P_{0} + ρ_{l} g H)}_{0}^{2 / 5}}{{[P_{0} + ρ_{l} g y]}_{0}^{7 / 5}}$
B $\frac{ρ_{l} n R g T_{0}}{{(P_{0} + ρ_{l} g H)}_{0}^{2 / 5} {[P_{0} ρ_{l} g (H - y)]}_{0}^{3 / 5}}$
C $ρ_{l} n R g T_{0} \frac{{(P_{0} + ρ_{l} g H)}_{0}^{3 / 5}}{{[P_{0} + ρ_{l} g y]}_{0}^{8 / 5}}$
D $\frac{ρ_{l} n R g T_{0}}{{(P_{0} + ρ_{l} g H)}_{0}^{3 / 5} {[P_{0} ρ_{l} g (H - y)]}_{0}^{2 / 5}}$
A small spherical monoatomic ideal gas bubble $(γ = 5 / 3)$ is trapped inside a liquid of density $ρ$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is $T_{0}$ , the height of the liquid is H and the atmospheric pressure $P_{0}$ (Neglect surface tension).

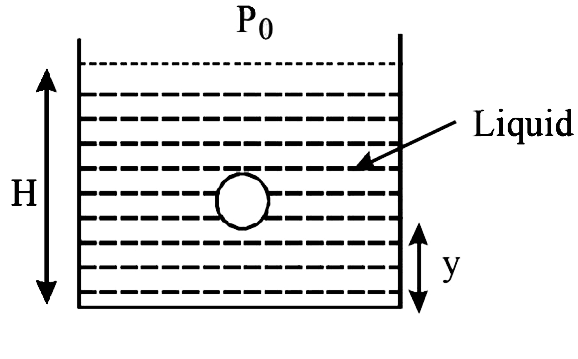
As the bubble moves upwards, besides the buyoncy force the following forces are acting on it
AOnly the force of gravity
BThe force due to gravity and the force due to the pressure of the liquid
CThe force due to gravity, the force due to the pressure of the liquid and the force due to viscocity of the liquid
DThe force due to gravity and the force due to viscocity of the liquid