A small square loop of wire of side y is placed inside a large square loop of side x(x>>y). The loops are coplanar and their centres coincide. Find the mutual inductance of the system.Solution in Bengali
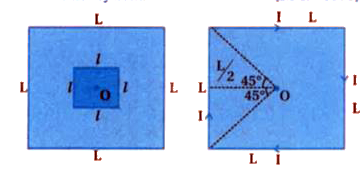
Let I be the current flowing through a square loop of side L.
Magnetic field at the centre of the loop, B=4B1
[where B1 is magnetic field at the centre of the loop due to one of its sides] Now, for the large square loop, L = x
∴B1=μ04π.Ix2(sin45∘+sin45∘) [∵ distance of the centre from each side of the large loop = x2]
=μ02π.Ix(1√2+1√2)=μ0I√2πx
∴B=4μ0I√2πx=2√2μ0Iπx
Now, magnetic flux linked with the small square loop,
ϕ=B× area of the small square loop
=B×y2=2√2μ0Iy2πx ... (1)
If M be the mutual inductance between the two loops,then
ϕ=MI ... (2)
From equations (1) and (2), M=2√2μ0y2πx
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - SECTION RELATED QUESTIONS29videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - HOTS19videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner13videos
ELECTRIC POTENTIAL
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVES EXERCISE - CBSE SCANNER17videos
ELECTROMAGNETIC WAVES
Similar Questions
What do you mean by electromagnetic induction?
09:02View SolutionA cylindrical bar magnet is placed along the axis of a circular coil. If the magnet is rotated about that axis, will any current be induced in the coil?
03:23View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.05:49View SolutionWhat are the directions of electric and magnetic field vectors relative to each other and relative to the direction of propagation of electromagnetic waves?
05:49View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
03:36View SolutionA small square loop of wire of side l is placed inside a large squre loop of wire of side L(>>l). The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
03:36View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l) .The loops are coplanar and their centers coincide.The mutual inductance of the system is proportional to
03:36View SolutionA small square loop of wire of side I is placed inside a large square loop of wire of side L(L>> I ) .The loops are coplanar and their centers coincide. The mutual inductance of the system is proportional to
04:42View SolutionA small square loop of wire of side 'I' is placed inside a large square loop of side L (L > I). If the loops are coplanar and their centres coincide, the mutual inducation of the system is directly proportional to
02:47View SolutionA small square loop of wire of side 'I' is placed inside a large square loop of side L (L > I). If the loops are coplanar and their centres coincide, the mutual inducation of the system is directly proportional to
View SolutionA small square loop of wire of side 'I' is placed inside a large square loop of side L (L > I). If the loops are coplanar and their centres coincide, the mutual inducation of the system is directly proportional to
05:01View SolutionA small square loop of wire of side l is placed inside a large square loop of side L. (L gt gt l) . The loops are coplanar and their centres coincide. The mutual induction of the system is :
03:28View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are coplanar and their centres coincide. Find the mutual inductance of the system.
 01:56View Solution
01:56View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L ( > > l) . The loops are coplanar and their centres coincide. What is the mutual inductance of the system?
View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L (L gt gt l) . The loops are coplanar and their centre coincide. What is the mutual inductance of the system ?
View Solution

