A small steel ball falls through a syrup at a constant speed of 10cms−1. If the steel ball is pulled upwards with a force equal to twice its effective weight, how fast will it move upwards?
10cms−1
20cms−1
5cms−1
zero
The correct Answer is:A
To solve the problem, we need to analyze the forces acting on the steel ball when it is pulled upwards with a force equal to twice its effective weight. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the forces acting on the ball
When the steel ball is falling through the syrup at a constant speed of 10 cm/s, it experiences three main forces:
1. Weight of the ball (W): This is the gravitational force acting downwards, given by W=mg, where m is the mass of the ball and g is the acceleration due to gravity.
2. Buoyant force (B): This is the upward force exerted by the syrup, which acts against the weight of the ball.
3. Viscous drag force (F_v): This is the resistance force due to the syrup, which also acts upwards.
At terminal velocity (constant speed), the net force acting on the ball is zero. Therefore, we can write:
W−B−Fv=0
This implies:
Fv=W−B
The effective weight of the ball is defined as:
Weffective=W−B
Step 2: Determine the effective weight
Since the ball is falling at a constant speed, the effective weight can be expressed as:
Weffective=Fv
Given that the ball is falling at a constant speed of 10 cm/s, we can denote this speed as v=10cm/s.
Step 3: Calculate the upward force applied
According to the problem, the steel ball is pulled upwards with a force equal to twice its effective weight:
Fup=2Weffective
Step 4: Analyze the net force when pulling the ball upwards
When the ball is pulled upwards, the forces acting on it are:
- The upward force Fup=2Weffective
- The downward forces, which include the weight of the ball W and the viscous drag force Fv.
The net force Fnet acting on the ball when it is pulled upwards can be expressed as:
Fnet=Fup−(W+Fv)
Substituting Fup and Fv:
Fnet=2Weffective−(W+Weffective)
Fnet=2Weffective−W−Weffective
Fnet=Weffective−W
Step 5: Determine the acceleration
The net force will cause the ball to accelerate upwards. According to Newton's second law:
Fnet=ma
Where a is the acceleration of the ball. Therefore:
Weffective−W=ma
Step 6: Calculate the upward speed
Since the ball was initially moving downwards at a constant speed of 10 cm/s, when it is pulled upwards with a force equal to twice its effective weight, it will start moving upwards. The new speed will be equal to the initial speed because the forces are balanced in a similar manner. Thus, the speed of the ball moving upwards will also be:
v=10cm/s
Conclusion
The steel ball will move upwards at a speed of 10 cm/s.
---
When the steel ball is falling through the syrup at a constant speed of 10 cm/s, it experiences three main forces:
1. Weight of the ball (W): This is the gravitational force acting downwards, given by W=mg, where m is the mass of the ball and g is the acceleration due to gravity.
2. Buoyant force (B): This is the upward force exerted by the syrup, which acts against the weight of the ball.
3. Viscous drag force (F_v): This is the resistance force due to the syrup, which also acts upwards.
W−B−Fv=0
This implies:
Fv=W−B
The effective weight of the ball is defined as:
Weffective=W−B
Since the ball is falling at a constant speed, the effective weight can be expressed as:
Weffective=Fv
Given that the ball is falling at a constant speed of 10 cm/s, we can denote this speed as v=10cm/s.
According to the problem, the steel ball is pulled upwards with a force equal to twice its effective weight:
Fup=2Weffective
When the ball is pulled upwards, the forces acting on it are:
- The upward force Fup=2Weffective
- The downward forces, which include the weight of the ball W and the viscous drag force Fv.
Fnet=Fup−(W+Fv)
Fnet=2Weffective−(W+Weffective)
Fnet=2Weffective−W−Weffective
Fnet=Weffective−W
The net force will cause the ball to accelerate upwards. According to Newton's second law:
Fnet=ma
Where a is the acceleration of the ball. Therefore:
Weffective−W=ma
Since the ball was initially moving downwards at a constant speed of 10 cm/s, when it is pulled upwards with a force equal to twice its effective weight, it will start moving upwards. The new speed will be equal to the initial speed because the forces are balanced in a similar manner. Thus, the speed of the ball moving upwards will also be:
v=10cm/s
The steel ball will move upwards at a speed of 10 cm/s.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Problems Based On Mixed Concepts34videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Assertion Reasoning20videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Pressure Difference And Capillarity23videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
A baseball of mass m is thrown upward with some initial speed. If air resistance is neglected, what is the force on the ball: (a) when it reaches half its maximum height, and (b) when it reaches its peak?
View SolutionA player throwsa a ball upwards with an initial speed of 29.4ms−1.
(i) What is the direction of acceleration during the upwared motion of the ball?
(ii) What are the velocity and acceleration of the ball at the highest point of its motion?
(iii) Choose the x=0 and t=0 to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of X-axis, and give the signs of positive, velocity and acceleration of the ball during its upward, and downward motion.
(iv) To what height does the ball rise and after how long does the ball return to the player's hand?( Take g=9.8ms−2, and neglect air resistance).View Solution
Knowledge Check
- Question 1 - Select One
A small steel ball bounces on a steel plate held horizontally. On each bounce the speed of the ball arriving at the plate is reduced by a factor e (coefficient of restitution) in the rebound, so that vupward=eVdownward. If the ball is initially dropped from a height of 0.4 m above the plate and if 10 seconds later the bouncing ceases, the value of e is
A√27B34C1318D1718 - Question 2 - Select One
A simple pendulum is made from a 0.65m long string and a small ball attached to its free end. The ball is pulled to one side through a small angle and then released from rest. After the ball is released, how much time elaspses before it attains its greatest speed?
A0.40sB0.10sC0.80sD0.20s - Question 3 - Select One
Consider the motion of a small spherical steel body of mass m, falling freely through a long column of a fluid that opposes its motion with a force proportional to its speed. Initially, the body moves down fast, but after some time attains a constant velocity known as terminal velocity. If weight mg, opposing force (F,) and buoyant force (Fb) act on the body, then the correct equation relating these forces, after the terminal velocity is reached, is :
Amg+Fv=FbBmg+Fv−FbCmg=Fv+FbDNone
A 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
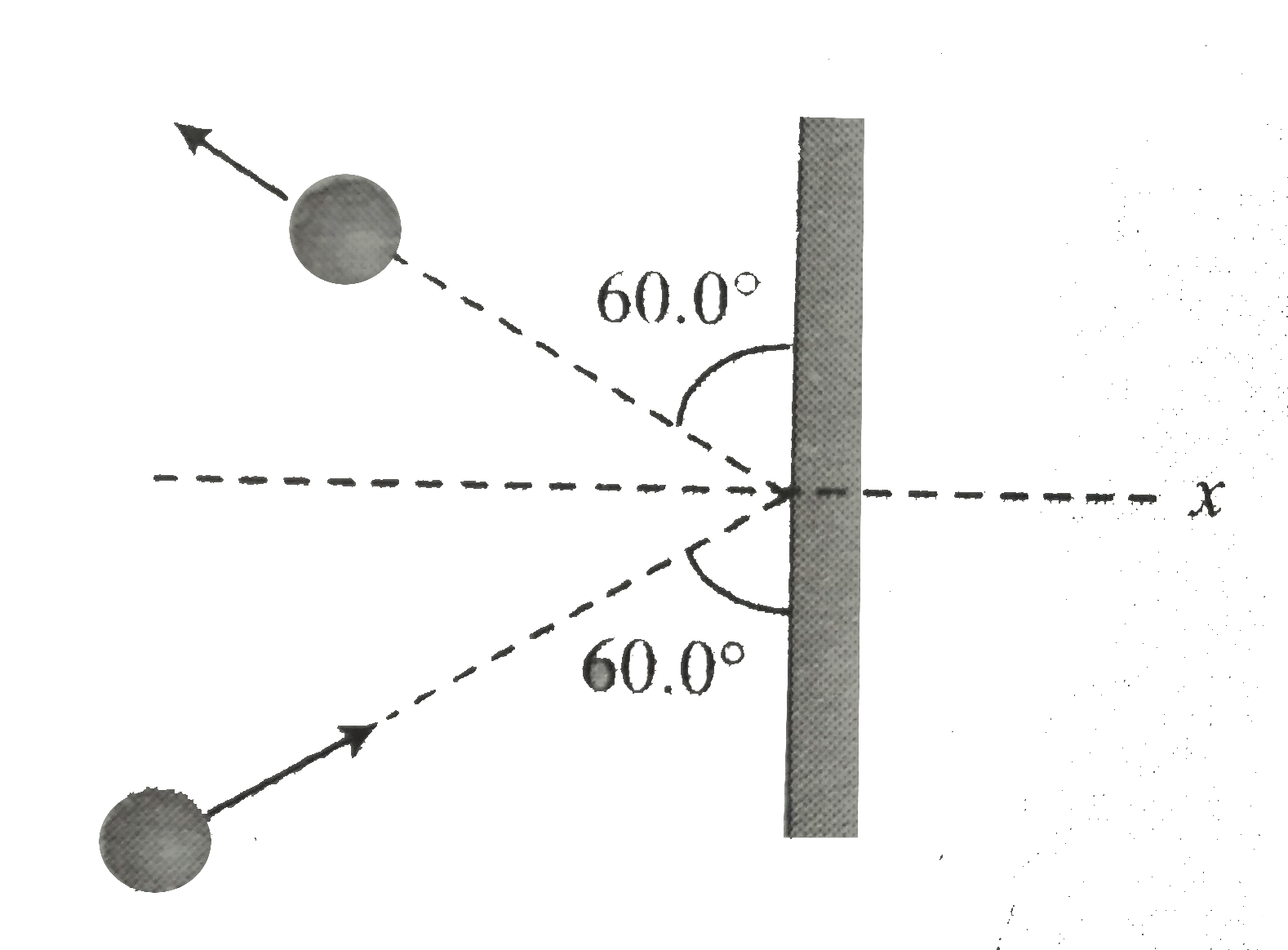 View Solution
View SolutionA small steel ball A is suspended by an inextensible thread of length l=1.5m from O. Another identical ball is thrown vertically downwards such that its surface remains just in contact with thread during downward motion and collides elastically with the suspended ball. If the suspended ball just completes vertical circle after collision, calculate the velocity (in cm/s) of the falling ball just before collision (g=10ms−2).
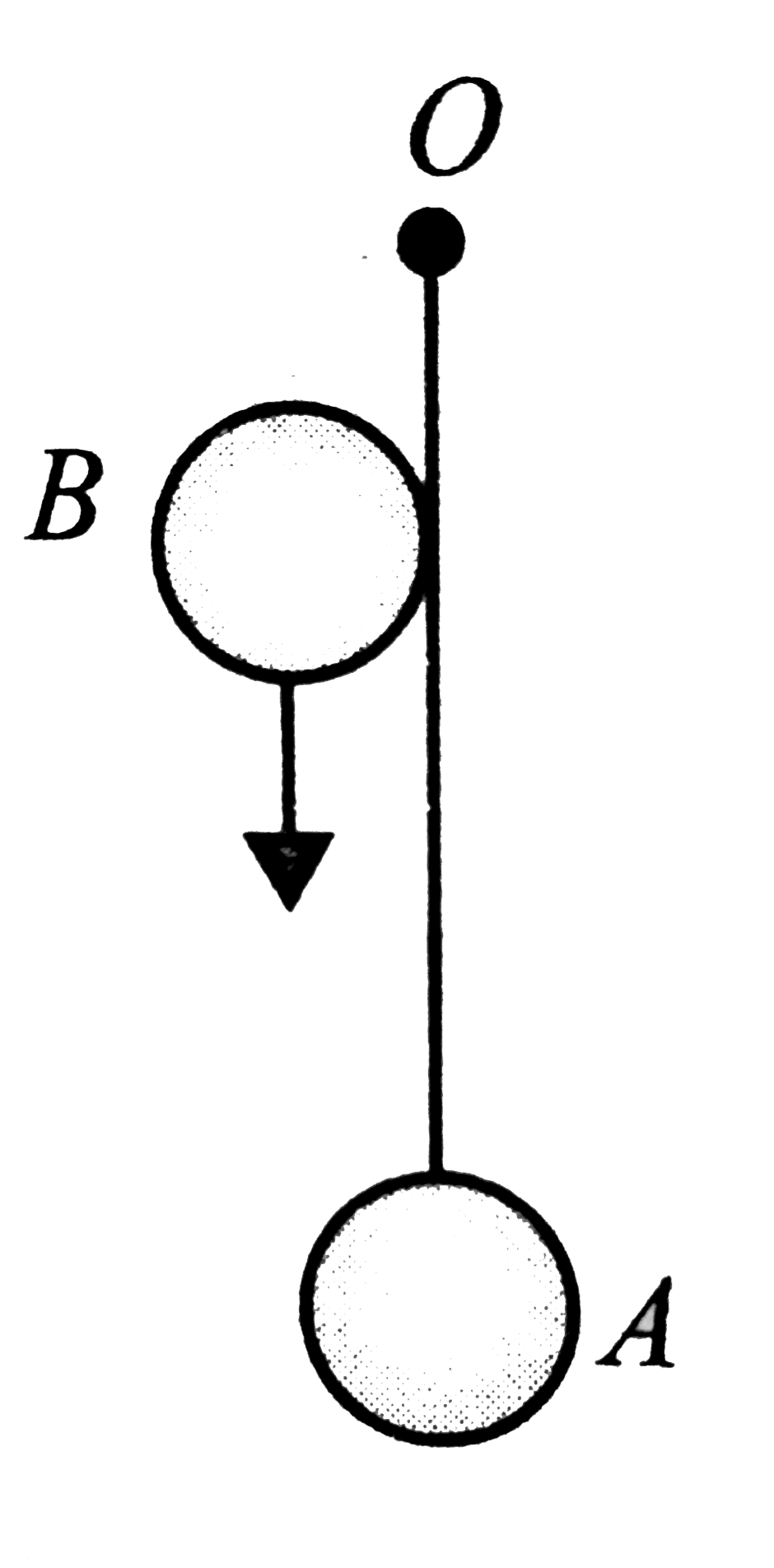 View Solution
View SolutionA boy standing on a stationary lift ( open from above ) thrown a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can , how hoes the ball take to return to his hands ?
View SolutionA ball is throw vertically upward. It has a speed of 10m/s when it has reached one half of its maximum height. How high does the ball rise ? (Taking g=10m/s2).
View SolutionA ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
View Solution

