A smooth block of mass m is released from rest from a height h. It slides and compresses the spring of stiffness k. Find the maximum compression of the spring .
Taking block spring a system. Now external force is doing work on system and no non-conservative force is present. The mechanincal energy should be conserved.
ΔK+ΔU=0
To solve the problem of finding the maximum compression of the spring when a block of mass m is released from a height h and compresses a spring of stiffness k, we can use the principle of conservation of mechanical energy. Here’s the step-by-step solution:
Step 1: Identify the energies involved
When the block is released from height h, it has gravitational potential energy and no kinetic energy since it starts from rest. As it falls and compresses the spring, the gravitational potential energy is converted into kinetic energy and then into spring potential energy at maximum compression.
Step 2: Write the expression for gravitational potential energy
The gravitational potential energy (U) at height h is given by:
U=mgh
Step 3: Write the expression for spring potential energy
The potential energy stored in the spring when it is compressed by a distance x is given by:
Uspring=12kx2
Step 4: Apply the conservation of mechanical energy
According to the conservation of mechanical energy, the total mechanical energy at the initial position (when the block is at height h) should equal the total mechanical energy at the point of maximum compression of the spring (when the block momentarily comes to rest):
Initial Energy=Final Energy
mgh=12kx2
Step 5: Solve for maximum compression x
Rearranging the equation to find x:
12kx2=mgh
kx2=2mgh
x2=2mghk
x=√2mghk
Final Answer
The maximum compression of the spring is:
x=√2mghk
---
When the block is released from height h, it has gravitational potential energy and no kinetic energy since it starts from rest. As it falls and compresses the spring, the gravitational potential energy is converted into kinetic energy and then into spring potential energy at maximum compression.
The gravitational potential energy (U) at height h is given by:
U=mgh
The potential energy stored in the spring when it is compressed by a distance x is given by:
Uspring=12kx2
According to the conservation of mechanical energy, the total mechanical energy at the initial position (when the block is at height h) should equal the total mechanical energy at the point of maximum compression of the spring (when the block momentarily comes to rest):
Initial Energy=Final Energy
mgh=12kx2
Rearranging the equation to find x:
12kx2=mgh
kx2=2mgh
x2=2mghk
x=√2mghk
The maximum compression of the spring is:
x=√2mghk
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass m is relesed from rest from a height h onto a smooth surface of mass M fitted with an ideal spring of stiffness k. find the maximum compression in the spring.

View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m strikes a light pan fitted with a vertical spring after falling through a distance h. If the stiffness of the spring is k, find the maximum compression of the spring.
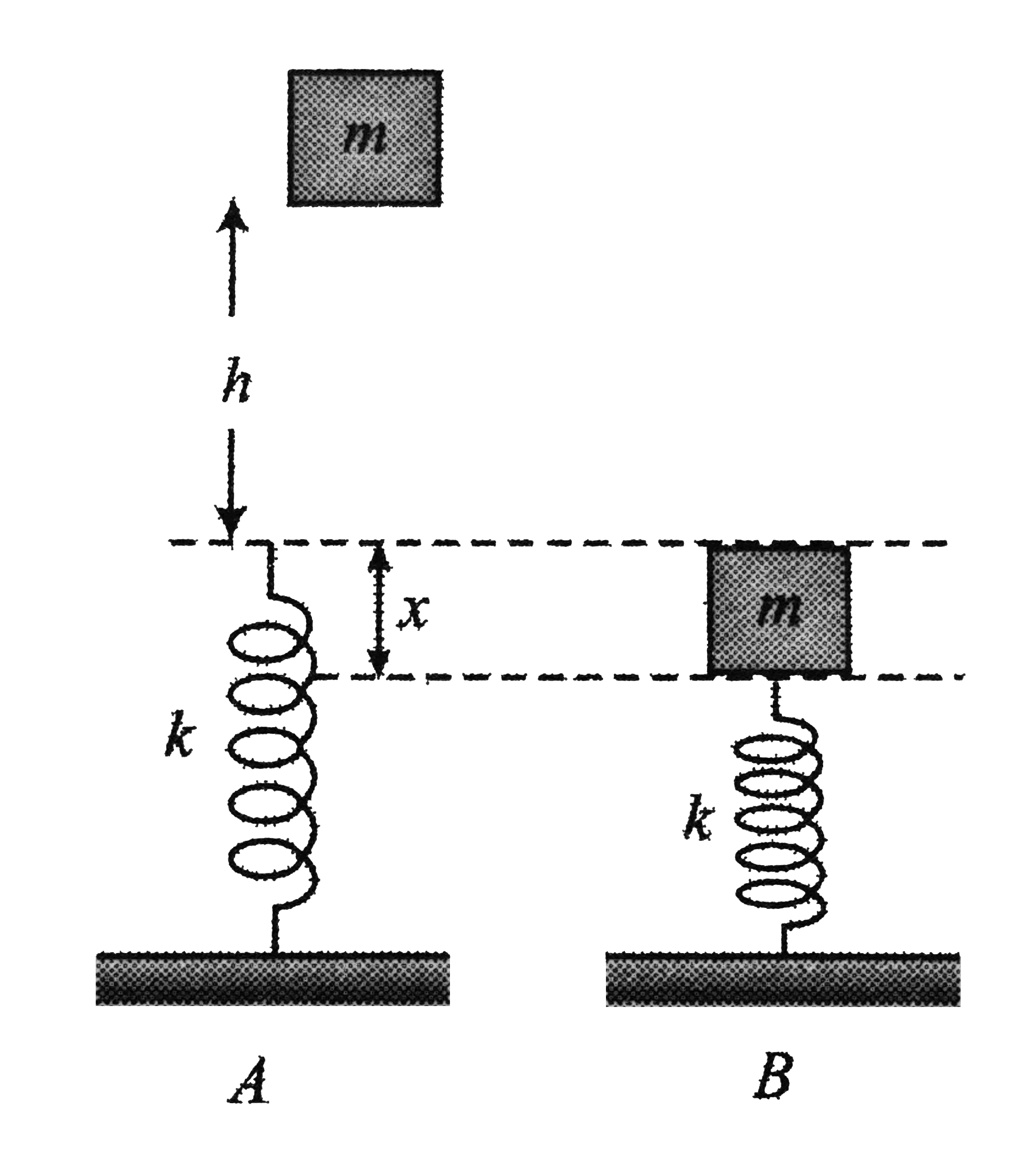
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

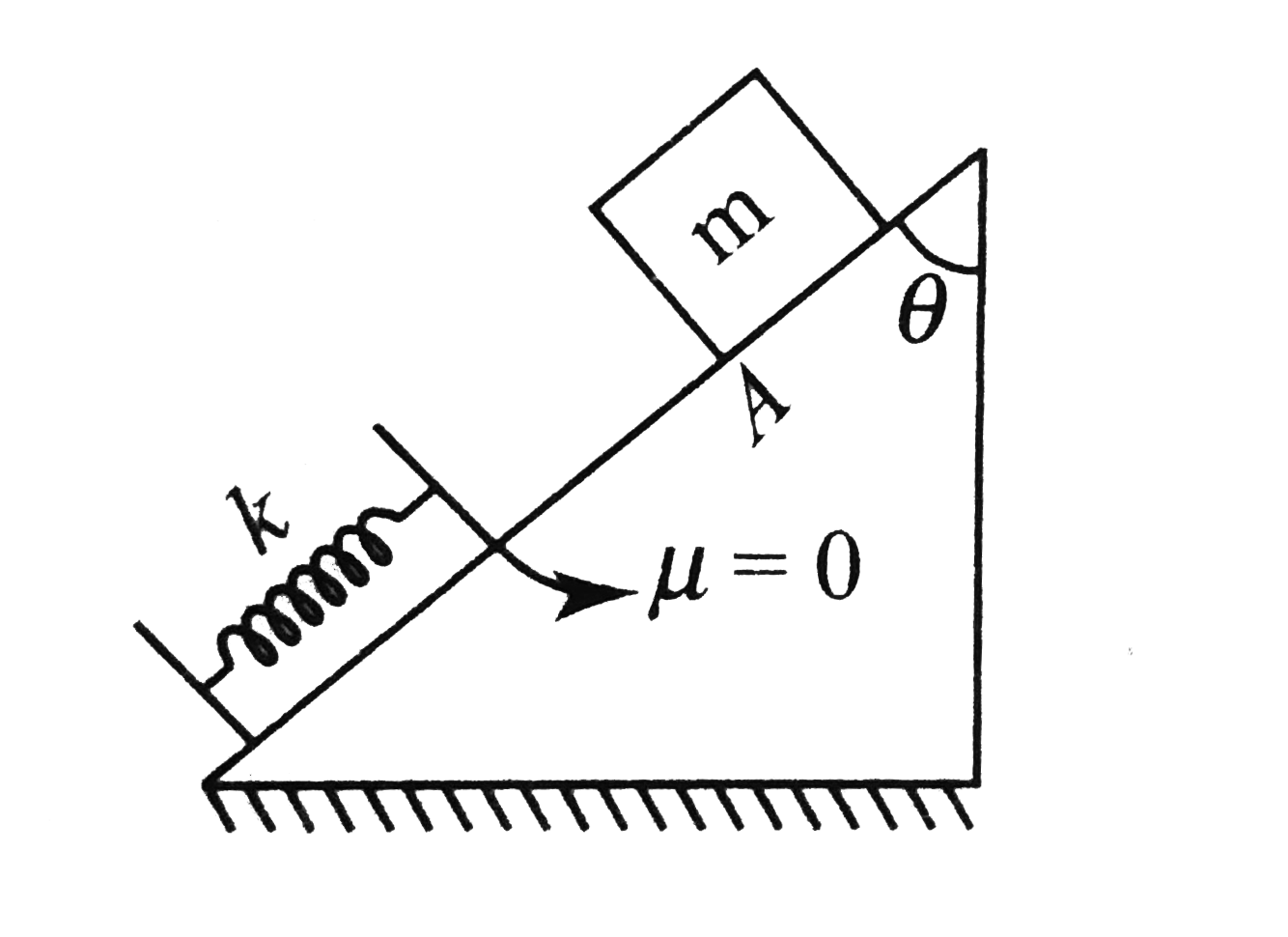
View SolutionA block of mass m is released from rest at point A. The compression in spring (force constant k) when the speed of block is maximum is found to be nmgcosθ4k. What should be the value of n?
View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?
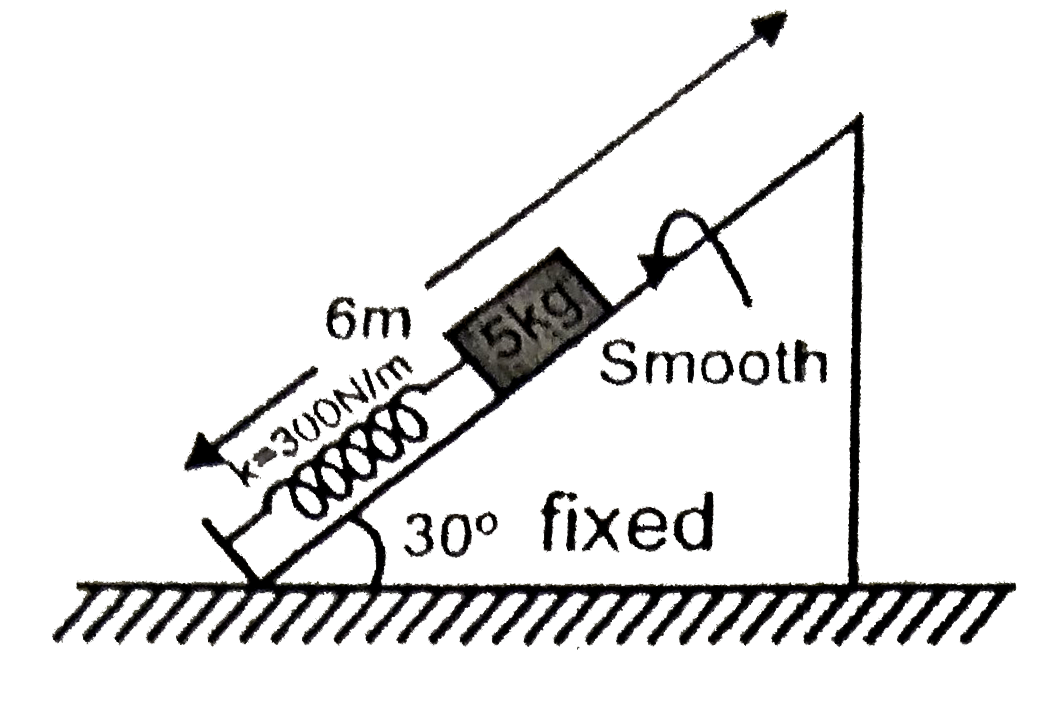
View SolutionA block of mass 5kg is released from rest when compression in spring is 2m. Block is not attached with spring and natural length of the spring in 4m. Maximum height of block from ground is :(g=10m/s2)
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionA block of mass 2 kg is dropped from a height of 40 cm on a spring whose force-constant 1960Nm−1. The maximum distance through which the spring is compressed by
View Solution
