A smooth chain (AB) of mass (m) rests against a surface in the form of a quarter of circle of radius R. If it is released from rest, the form of a quarter of a circle of radius R. If it is releaded from, the velocity of the chain after it comes over the horizontal part of the surface is .

(a)
(b)
(c)
(d)
The correct Answer is:C
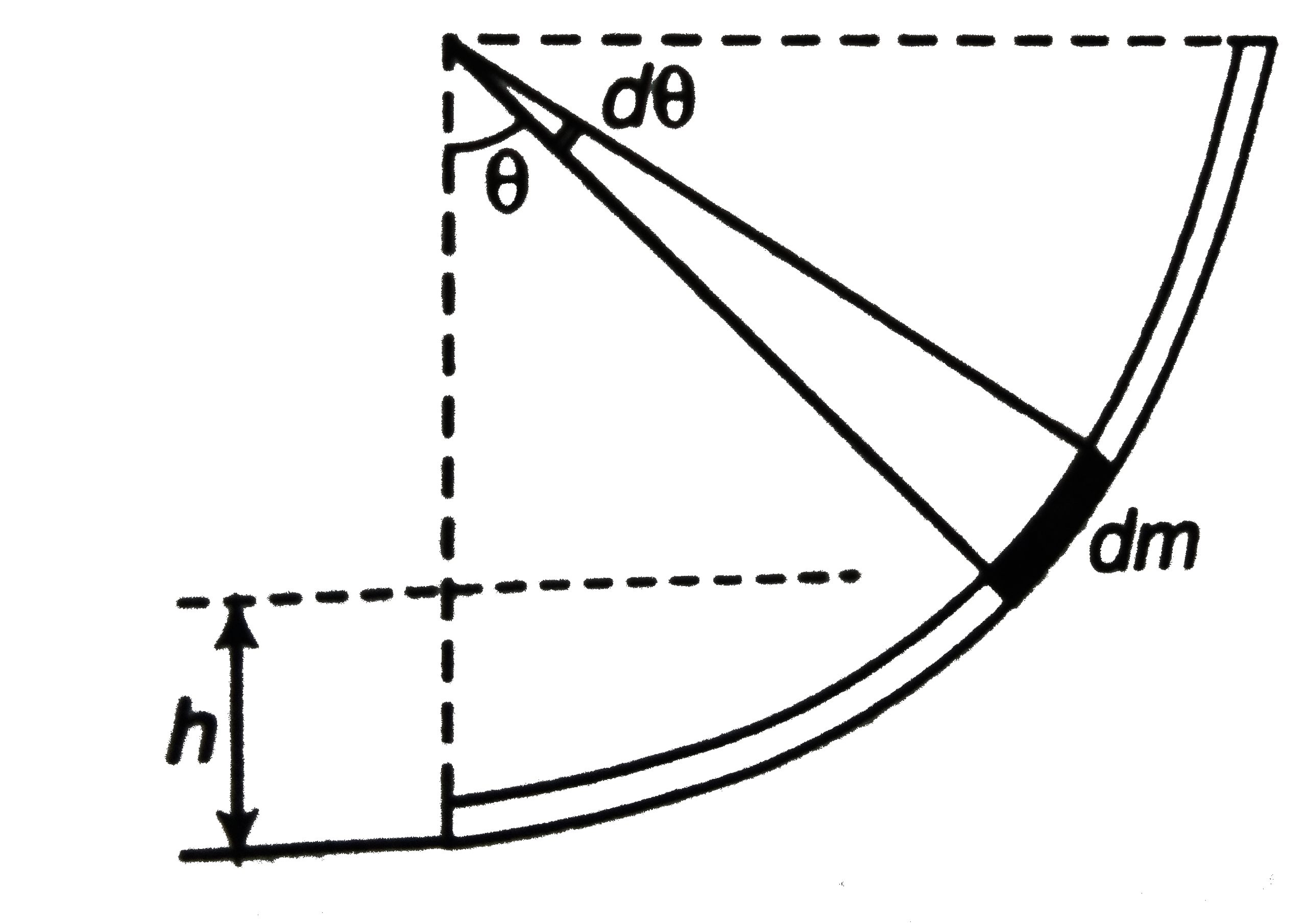
Now,
or
Similar Questions
A chain AB of length equal to the quarter of a circle of radius R is placed on a smooth hemisphere as shown in figure -3.66. When it is released, it starts falling. Find the velocity of the chain when it falls of the end B from the hemisphere.

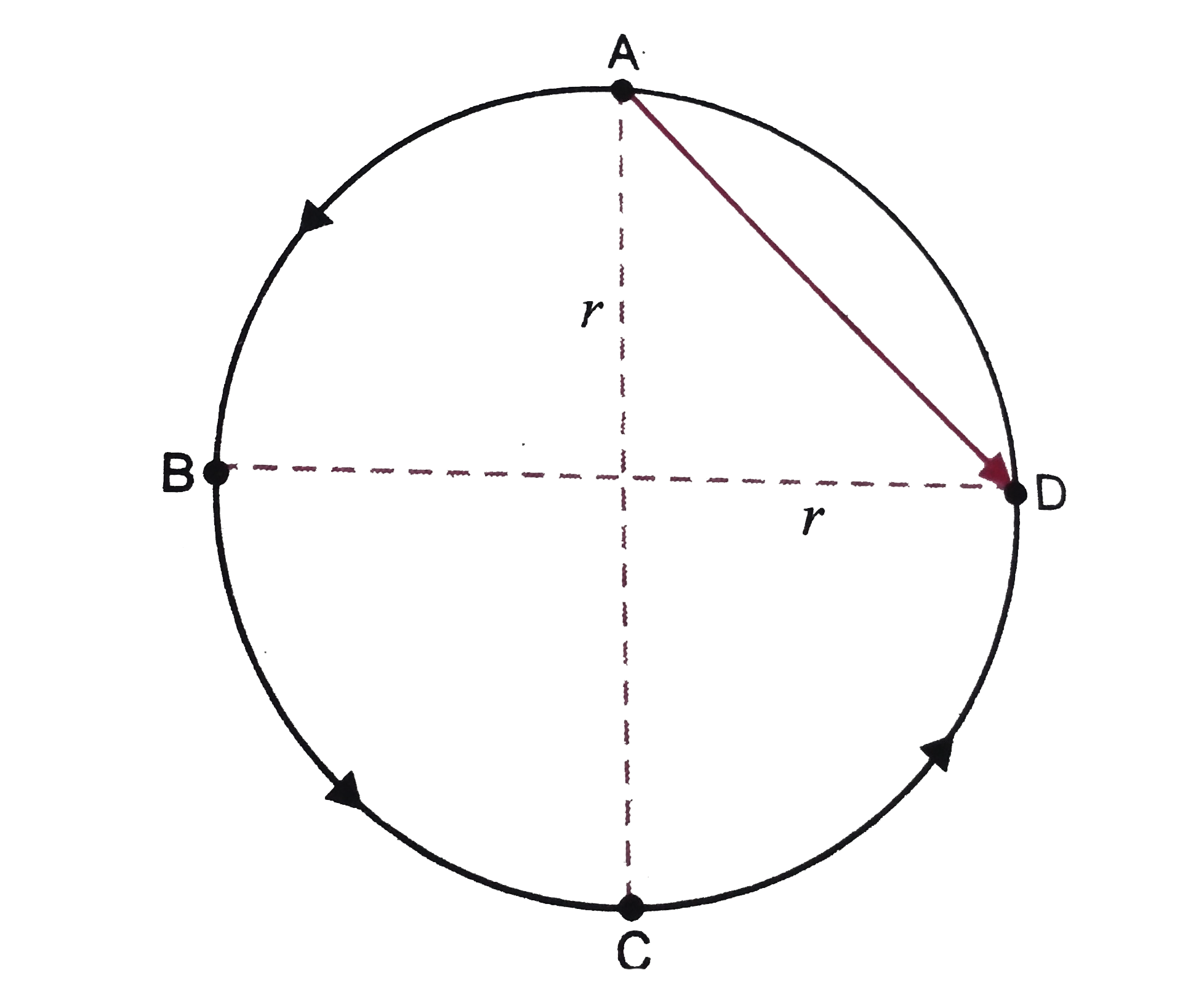
View SolutionA particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?
View Solution
Knowledge Check
A ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
.A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)A small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
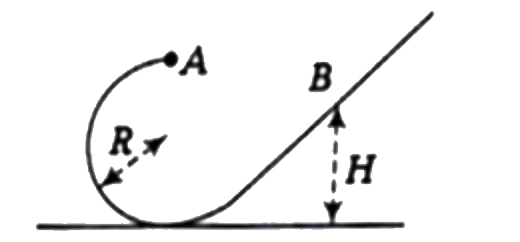 ARB2 RC3R2D5R2
ARB2 RC3R2D5R2Starting from rest, a particle rotates in a circle of radius R 2 m with an angular acceleration = /4 rad/s2.The magnitude of average velocity of the particle over the time it rotates quarter circle is:
A1.5m/sB2m/sC1m/sD1.25m/s
A particle moves over three quarters of a circle of radius r. What is the magnitude of its displacement ?

View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View SolutionA roadway bridge over a rivulet is in the form of quarter of a circle of radius 60 m. What is the maximum speed with which a car can pass over the bridge without leaving the ground at any point ?
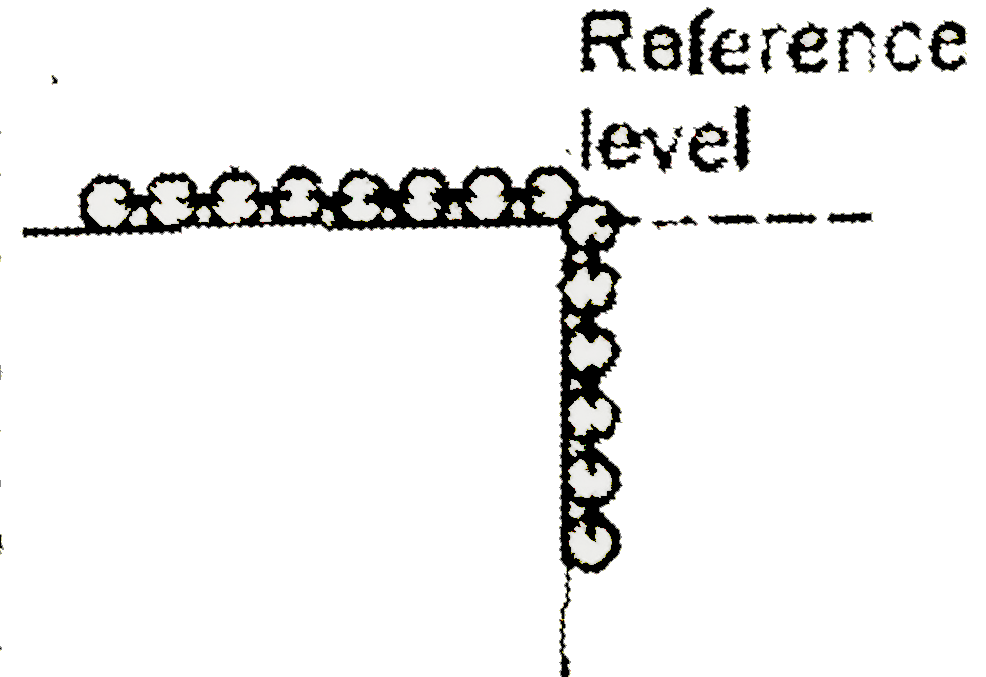
View SolutionA uniform chain of length 1 and mass m is kept on a smooth table. It is released from rest when the overhaning part was nth fraction of total length. Find the kinetic energy of the chain as it completely slips off the table
View SolutionA particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
View Solution
