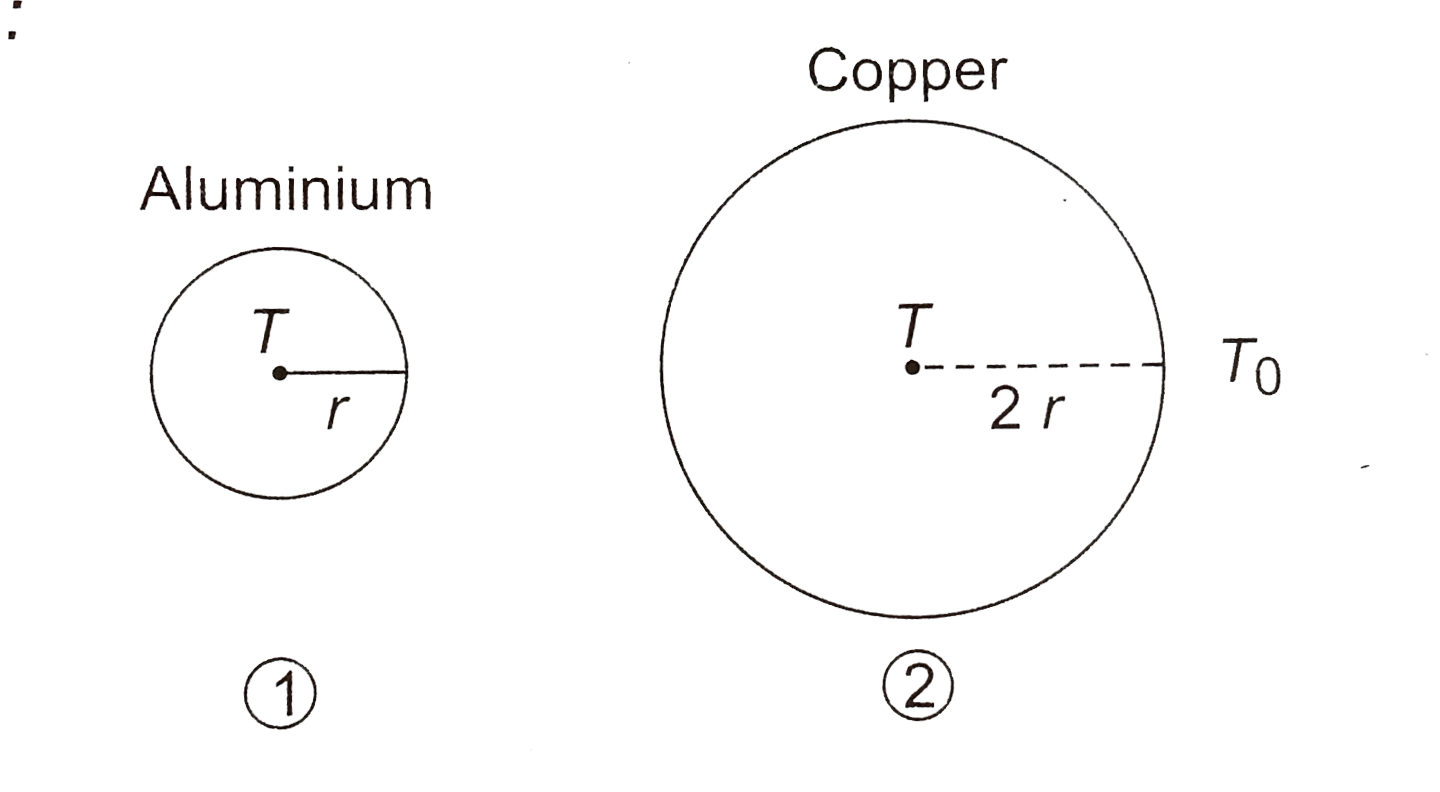
A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperature. Assume that the emissivity of both the spheres is the same. Find the ratio of
(a) the rate of heat from the aluminium sphere to the rate of heat loss from the copper sphere and
(b) the rate of fall of temperature of the the aluminium sphere to the rate of fall temperature of teh copper sphere. The specific heat capacity of aluminium =900J/kg−∘C and that of copper =390J/kg−∘C. The density of copper is 3.4 times the density of aluminium.
(a) u1u2=eσA1T4eσA2T4=r21r22=(r2r)2=14
(b) Rate of fall of temperature
dTdt=eσAms(T4−T40)
=eσ4πr2ρ43πr3s(T4−T40)
=3eσρrs(T4−T40)
(dT/dt)(dT/dt)=ρ2r2s2ρ1r1s1=(3.4)(2rr)(390900)
=2.951

Topper's Solved these Questions
Similar Questions
A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emisssivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of heat loss from the copper sphere and (b) the rate of fall of temperature of the aluminium sphere to the rate of fall of temperature of copper sphere. The specific heat capacity of aluminium =900Jkg−1C−1 . and that of copper =390Jkg−1C−1 . The density of copper =3.4 times the density of aluminium.
View SolutionA solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emissivity of both the spheres is the same. Find ratio of (a) the rate of heat loss from the aluminium sphere to the rate of all of temperature of the copper sphere. The specific heat capacity of aluminium =900Jkg−1^(@)C^(-1).andtˆofcopper=390Jkg^(-1)^(∘)C−1 . The density of copper =3.4 times the correct wattage.
View Solution
Knowledge Check
A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature.
ABoth will emit equal amount of radiation per unit time in the beginning.BBoth will absorb equal amount of radiation from the surrounding in the beginning.CThe initial rate of cooling (dTdt) will be the same for the two spheres.DThe two spheres will have equal temperature at any instant.A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature
Aboth will emit equal amount of radiation per unit time in the beginningBboth will absorb equal amount of radiation per second from the surroundings in the beginningCthe initial rate of cooling will be the same for both the spheresDthe two spheres will have equal temperatures at any instantA solid sphere and a hollow sphere of the same material and size are heated to the same temperature and allowed to cool in the same surroundings. If the temperature difference between the surroundings and each sphere is T, then :
AThe hollow sphere will cool at a faster rate for all values of TBThe solid sphere will cool at a faster rate for all values of TCBoth spheres will cool at the same rate for all values of TDBoth spheres will cool at the same rate only for small values of T
A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature.
View SolutionA solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature
View SolutionTwo spheres of same material and radius r and 2r are heated to same temperature and are kept in identical surroundings, ratio of their rate of loss of heat is
View SolutionTwo spheres of same material and radius r and 2r are heated to same temperature and are kept in identical surroundings, ratio of their rate of loss of heat is
View SolutionA solid sphere and a hollow sphere of same material and size are heated to same temperature and allowed to cool in the same surroundings. If the temperature difference between each sphere and its surrounding is T, then
View Solution
