A solid cube floats in water half immersed and h small vertical oscillations of time period π5s. Find the mass (in kg) (Take g=10m/s2.
4
2
1
0.5
The correct Answer is:A
(a) Since, the cube is half immersed. The density of cube should be half the density of water, i.e., 500kgm−3
T=2π√mρuAg (k=ρuAg)
π5=2π√a3×ρρw×a2×g
∴aρgρw=1100
∴a20=1100 or a=(0.2)m
Now, m=a3ρ=4kg (∵ Mass =Density × Volume)
Similar Questions
A cubical body (side 0.1m and mass 0.002kg) floats in water. It is pressed and then released so that it executes SHM. Find the time period. (g=10m/s2)
View SolutionA solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
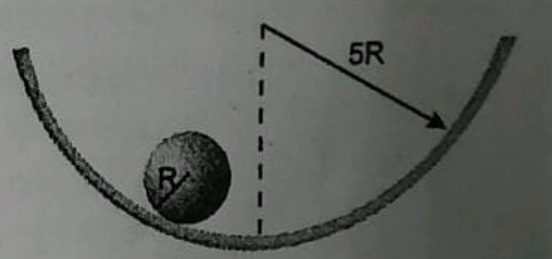
View Solution
Knowledge Check
An ice-cube of edge is 10 cm floating in water. Time period of small vertical oscillations of the cube is: (Specific gravity of ice is 0.9)
A0.6sB1.6sC2.4sD3.6sA spring balance has a scale that reads from 0 to 50 kg. the length of the scale is 20 cm. a block of mass m is suspended from this balance, when displaced annd released, it oscillates with a period 0.5 s. the value of m is (Take g=10ms−2)
A8 kgB12 kgC16 kgD20 kgA stone of mass 1 kg is tied to a string 2m long and it's rotated at constant speed of 40 ms−1 in a vertical circle. The ratio of the tension at the top and the bottom is
[Take g=10ms2]A8179B7981C1912D1219
A rocket of total mass 1000kg initially is launched from ground. The gases are ejected at the rate 20kg/s with velocity 1000 m/s relative to rocket vertically downwards. The initial acceleration of the rocket is a (in m/s2). Findag. (Take g=10m/s2)
View SolutionA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
View SolutionThe time period of oscillation of a particle in S.H.M. depends
View SolutionA load of mass 100 gm increases the length of wire by 10 cm. If the system is kept in oscillation, its time period is (g=10m/s2)
View SolutionA simple pendulum of length 1 m is freely suspended from the ceiling of an elevator. The time period of small oscillations as the elevator moves up with an acceleration of 2m/s2 is (use g=10m/s2)
View Solution
