A solid cylinder of length l and cross-sectional area A is made of a material whose resistivity depends on the distance r from the axis of the cylinder as ρ=k/r2 where k is constant . The resistance of the cylinder is -
πklA2
2πklA2
πklA
None
The correct Answer is:B
To find the resistance of a solid cylinder with a resistivity that depends on the distance from the axis, we can follow these steps:
1. Understand the given information:
- The resistivity of the material is given by ρ=kr2, where k is a constant and r is the distance from the axis of the cylinder.
- The cylinder has a length l and a cross-sectional area A.
2. Consider a differential element:
- We will consider a thin cylindrical shell of thickness dr at a distance r from the axis. The area of this shell is dA=2πrdr.
3. Calculate the resistance of the differential element:
- The resistance dR of this thin shell can be expressed as:
dR=ρdldA
- Substituting the values, we have:
dR=kr2⋅l2πrdr
- Simplifying this, we get:
dR=k⋅l2πr3dr
4. Integrate to find total resistance:
- To find the total resistance R, we need to integrate dR from r=R1 (inner radius) to r=R2 (outer radius):
R=∫R2R1dR=∫R2R1k⋅l2πr3dr
- The integral of 1r3 is:
∫1r3dr=−12r2
- Thus, we have:
R=k⋅l2π(−12r2)R2R1
- Evaluating the limits:
R=k⋅l2π(−12R22+12R21)
- This simplifies to:
R=k⋅l4π(1R21−1R22)
5. Final expression for resistance:
- If we assume the cylinder is solid (i.e., R1=0 and R2=R), we can express the total resistance as:
R=2klA
- Where A is the cross-sectional area of the cylinder.
Final Answer:
The resistance of the cylinder is given by:
R=2klA
- The resistivity of the material is given by ρ=kr2, where k is a constant and r is the distance from the axis of the cylinder.
- The cylinder has a length l and a cross-sectional area A.
- We will consider a thin cylindrical shell of thickness dr at a distance r from the axis. The area of this shell is dA=2πrdr.
- The resistance dR of this thin shell can be expressed as:
dR=ρdldA
- Substituting the values, we have:
dR=kr2⋅l2πrdr
- Simplifying this, we get:
dR=k⋅l2πr3dr
- To find the total resistance R, we need to integrate dR from r=R1 (inner radius) to r=R2 (outer radius):
R=∫R2R1dR=∫R2R1k⋅l2πr3dr
- The integral of 1r3 is:
∫1r3dr=−12r2
- Thus, we have:
R=k⋅l2π(−12r2)R2R1
- Evaluating the limits:
R=k⋅l2π(−12R22+12R21)
- This simplifies to:
R=k⋅l4π(1R21−1R22)
- If we assume the cylinder is solid (i.e., R1=0 and R2=R), we can express the total resistance as:
R=2klA
- Where A is the cross-sectional area of the cylinder.
The resistance of the cylinder is given by:
R=2klA
Topper's Solved these Questions
Similar Questions
A long round conductor to cross-sectional area S is made of material whose resistivity depends only on a distance r from the axis of the conductor as ρ=α/r4, where α is a constant. Find :
(a) the resistance per unit length of such a conductor,
(b) the electric field strength in the conductor due to which a current I flow though it.
View SolutionA long cylindrical conductor of cross-sectional area A and radius a is made of material whose resistivity depends only on a distance r from the axis of conductor, given by ρ=cr2, where c is a constant. Find the resistance per unit length of the conductor and the electric field strength due to which a current I flows in it.
View Solution
Knowledge Check
A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
AE=14π∈0K⋅qr2BE=12π∈0k⋅qrLCE=σ/∈0kDnone of theseA solid cylindrical wire of length l has cross-section radius a as shown below. The specific resistance of material is given as ρ=ρ0r, where r is distance from axis of cylinder and ρ0 is a positive constant quantity. The resistance across its ends is :
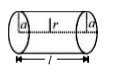 Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπ
Aρ0l2πaBρ0lπa2Cρ0lπaD2ρ0lπA conductor of length l and area of cross-section A has a resistance R then its specific resistance is
Aρ=RAlBρ=RAlCρ=lRADρ=R2Al
A very long, solid insulating cylinder with radius R has a cylindrical hole with radius a bored along its entire length. The axis of the hole is at a distance b from the axis of the cylinder, where a<b<R (as shown in figure). The solid material of the cylinder has a uniform volume charge density ρ. Find the magnitude and direction of the electric field inside the hole, and show that this is uniform over the entire hole.
 .
.
View SolutionA dielectric cylinder of radius a is infinitely long. It is non-uniformly charged such that volume charge density ρ varies directly as the distance from the cylinder. Calculate the electric field intensity due to it at a point located at a distance r from the axis of the cylinder. Given that ρ is zero at the axis and it is equal to ρ on the surface of cylinder. Also calculate the potential difference between the axis and the surface. [ρr23∈0a,ρa29∈0]
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
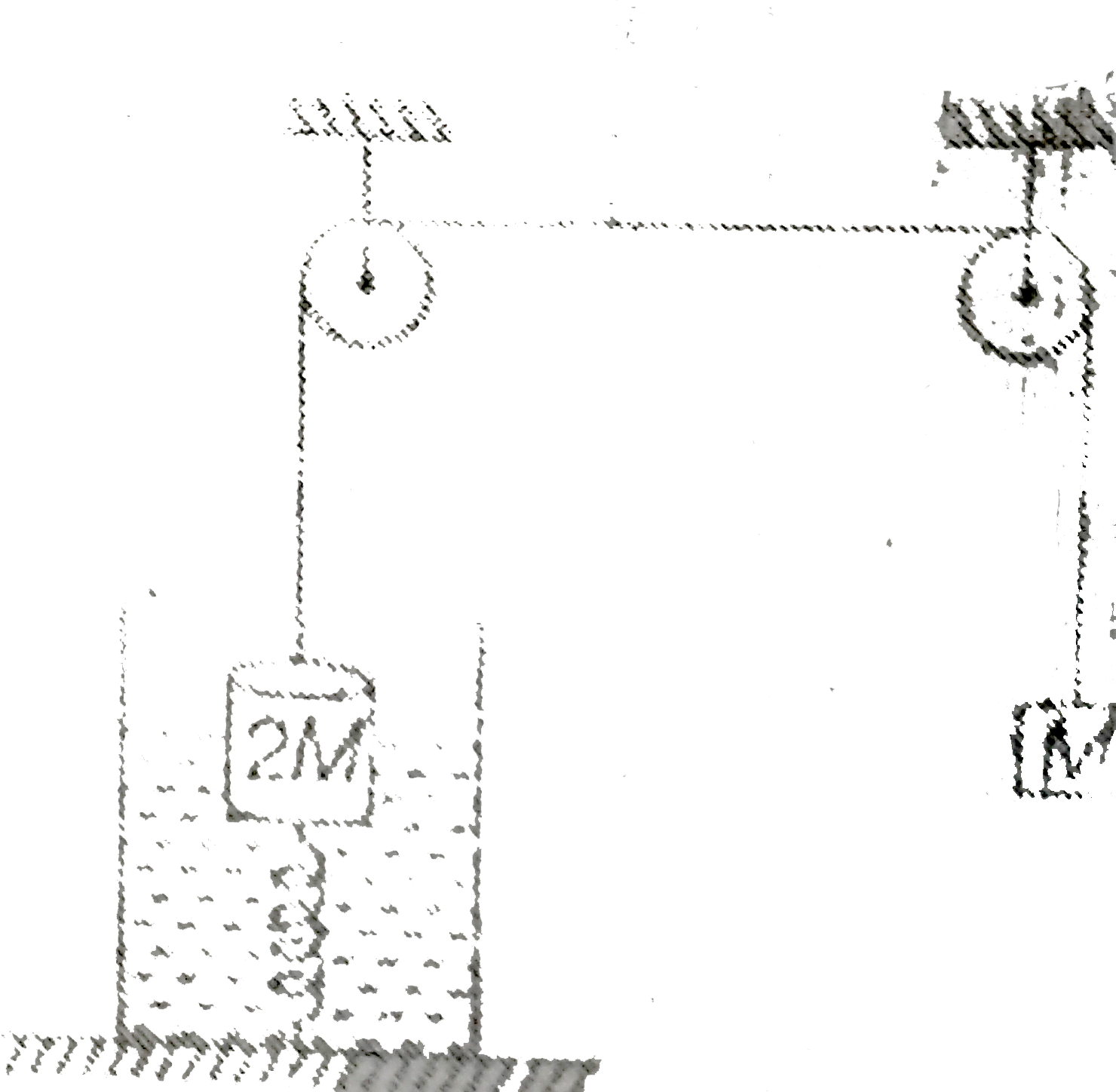
Under equilibrium conditions
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
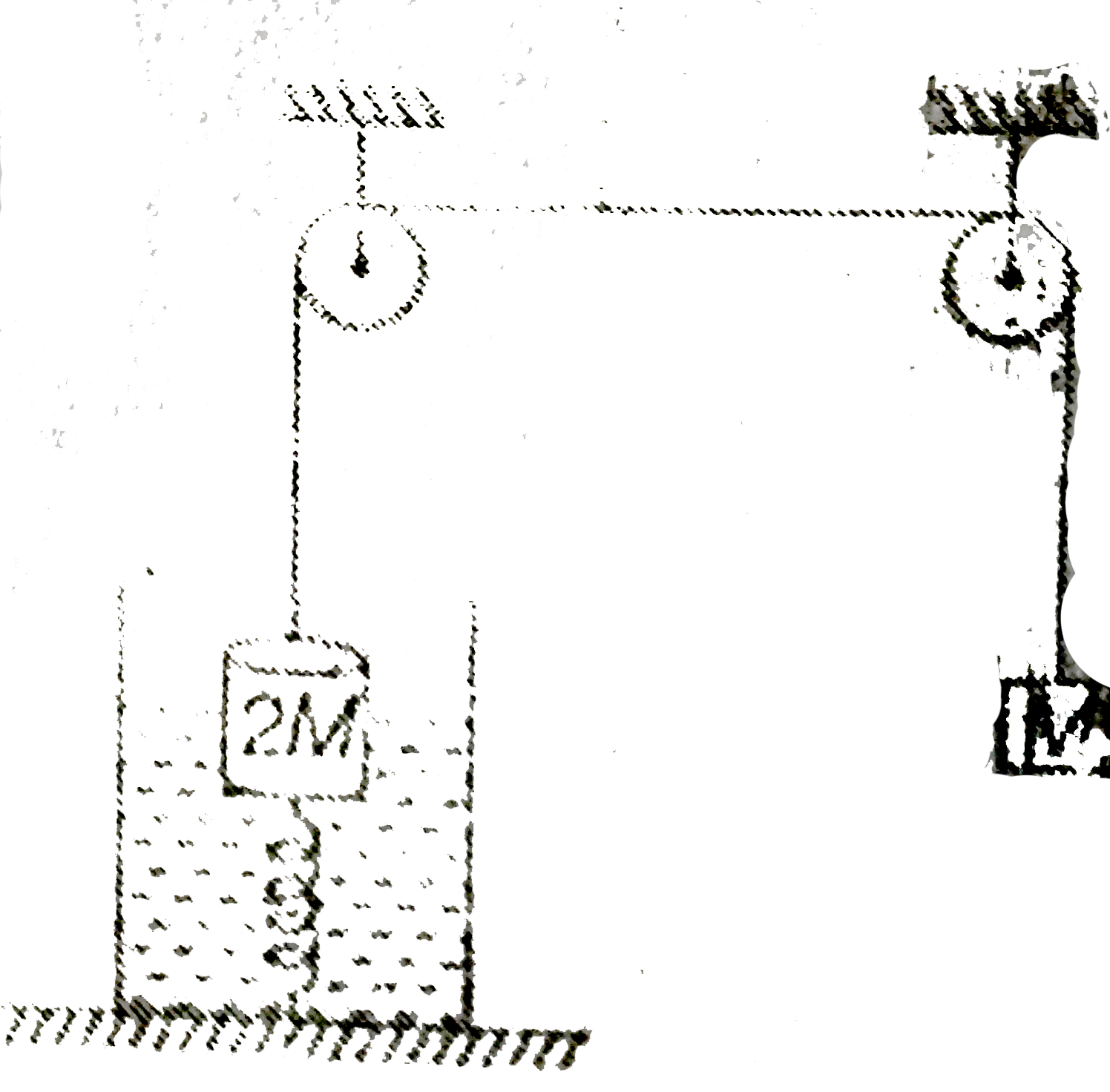
If the cylinder is pushed down from equilibrium by a distance which is half the distance as calculated in the above question, determine time period of subsequent motion.
View Solution0.5 mole of an ideal gas at constant temperature 27∘C kept inside a cylinder of length L and cross-section area A closed by a massless piston The cylinder is attached with a conducting rod of length L cross-section area (1/9)m2 and thermal conductivity k whise other end is maintained at 0∘C If piston is moved such that rate of heat flow through the conducing rod is constant then find velocity of piston when it is at height L/2 from the bottom of cylinder [Neglect any kind of heat loss from system
 .
.
View Solution
