A solid of density D is floating in a liquid of density d. If υ is the volume of solid submerged in the liquid and V is the total volume of the solid, then υ/V equal to
dD
Dd
DD+d
D+dD
The correct Answer is:B
To solve the problem, we need to apply the principles of buoyancy and the relationship between the densities of the solid and the liquid.
1. Understand the Concept of Buoyancy:
When a solid floats in a liquid, the weight of the solid is balanced by the buoyant force (upthrust) acting on it. This is known as Archimedes' principle.
2. Write the Weight of the Solid:
The weight of the solid can be expressed as:
W=Volume×Density×g=V×D×g
where V is the total volume of the solid, D is the density of the solid, and g is the acceleration due to gravity.
3. Write the Buoyant Force:
The buoyant force (upthrust) acting on the solid is equal to the weight of the liquid displaced by the submerged part of the solid. This can be expressed as:
Fb=Volume submerged×Density of liquid×g=υ×d×g
where υ is the volume of the solid submerged in the liquid and d is the density of the liquid.
4. Set the Weight Equal to the Buoyant Force:
Since the solid is floating, the weight of the solid is equal to the buoyant force:
V×D×g=υ×d×g
We can cancel g from both sides:
V×D=υ×d
5. Rearranging the Equation:
We can rearrange the equation to find the ratio of the submerged volume to the total volume:
υV=Dd
6. Final Result:
Therefore, the ratio of the volume of the solid submerged in the liquid to the total volume of the solid is given by:
υV=Dd
When a solid floats in a liquid, the weight of the solid is balanced by the buoyant force (upthrust) acting on it. This is known as Archimedes' principle.
The weight of the solid can be expressed as:
W=Volume×Density×g=V×D×g
where V is the total volume of the solid, D is the density of the solid, and g is the acceleration due to gravity.
The buoyant force (upthrust) acting on the solid is equal to the weight of the liquid displaced by the submerged part of the solid. This can be expressed as:
Fb=Volume submerged×Density of liquid×g=υ×d×g
where υ is the volume of the solid submerged in the liquid and d is the density of the liquid.
Since the solid is floating, the weight of the solid is equal to the buoyant force:
V×D×g=υ×d×g
We can cancel g from both sides:
V×D=υ×d
We can rearrange the equation to find the ratio of the submerged volume to the total volume:
υV=Dd
Therefore, the ratio of the volume of the solid submerged in the liquid to the total volume of the solid is given by:
υV=Dd
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionMore is the density of a liquid than a solid, more the volume of solid will submerge in it.
View Solution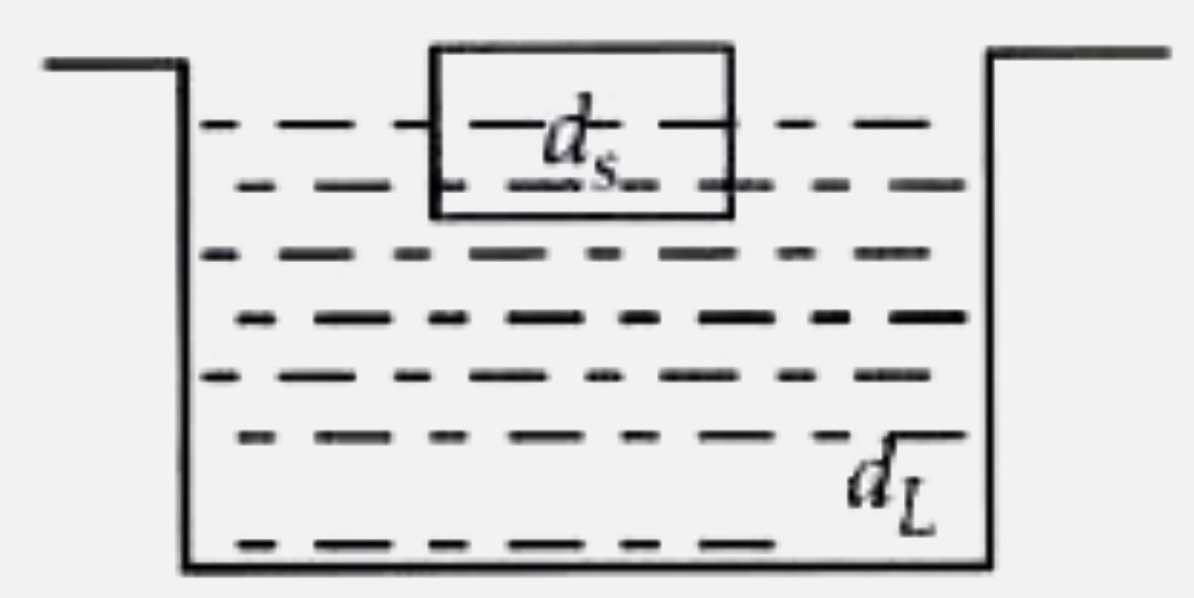
The figure above shows a solid of density dS floating in a liquid of density dL.
The same solid floats in water with 3th5 of its volume immersed in it. Calculate the density of the solid. (density of water = 1 g cm−3 )
View Solution
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the relation between dS and dL in the above case?
View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

View SolutionA solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionA block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA solid whose volume does not change with temperature floats in a liquid. For two different temperatures t1 and t2 of the liqiud, fraction f1 and f2 of the volume of the solid remain submerged in the liquid. The coefficient of volume expansion of the liquid is equal to
View SolutionA solid cube floats in a liquid of density ρ with half of its volume submerged as shown. The side length of the cube is a, which is very small compared to the size of the container. Now a liquid of density ρ3 (immiscible with the liquid already in the container) is poured slowly into the container. The column of the liquid of density ρ3 that must be poured so that the cube is fully submerged (with its top surface coincident with the surface of the poured liquid) is :

View Solution
