A solid sphere of mass m and radius r initially placed at a distance 5r from the centre of a point mass M as shown in figure. Now During displacement, it is also uniformly expanded to a radius 2 r so that its density decreases uniformly throughout its volume. Find the work required in this process.

Step by step video & image solution for A solid sphere of mass m and radius r initially placed at a distance 5r from the centre of a point mass M as shown in figure. Now During displacement, it is also uniformly expanded to a radius 2 r so that its density decreases uniformly throughout its volume. Find the work required in this process. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Particle Exercise
50 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Discussion Qns
31 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
Similar Questions
Knowledge Check
A shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
A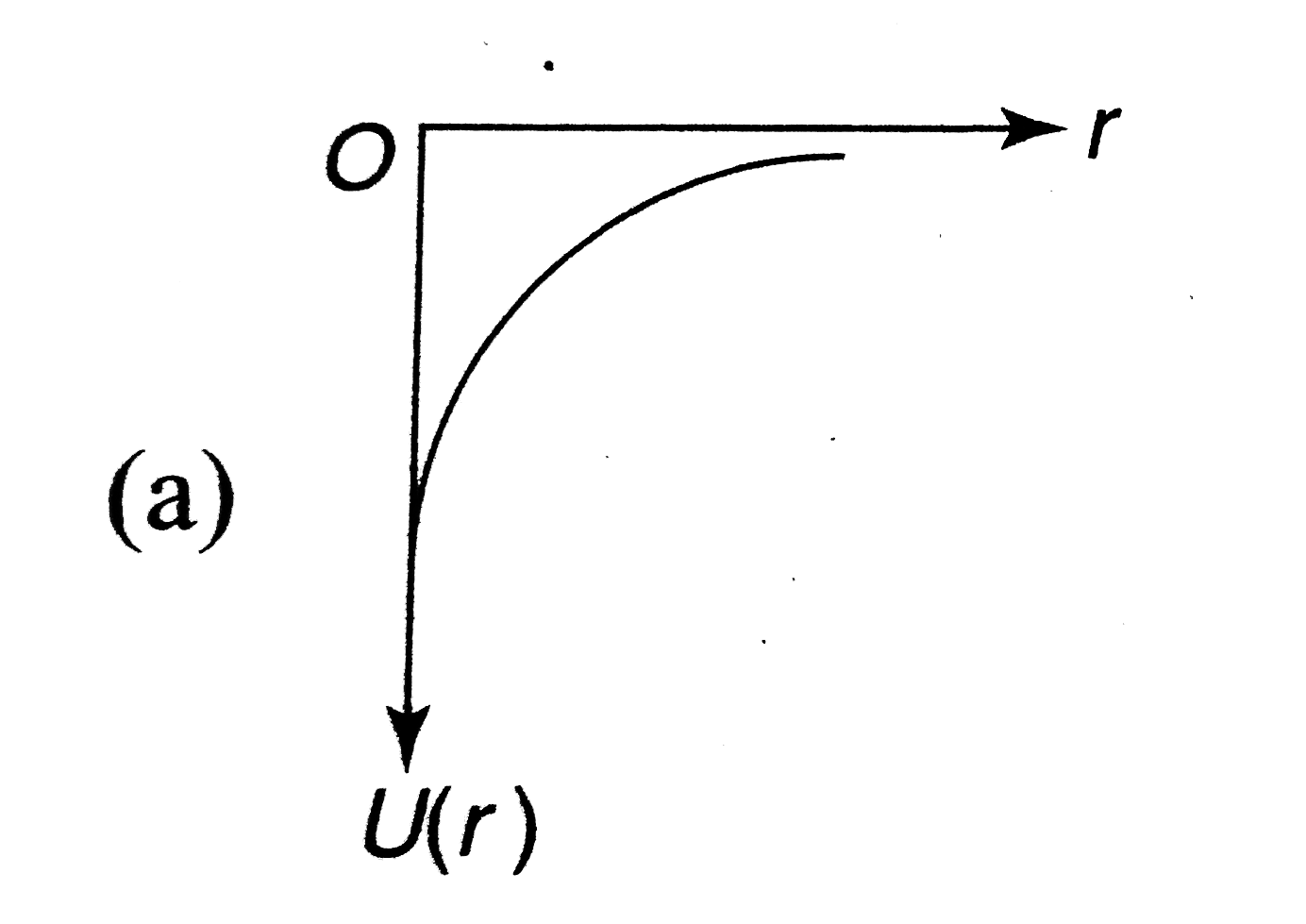 B
B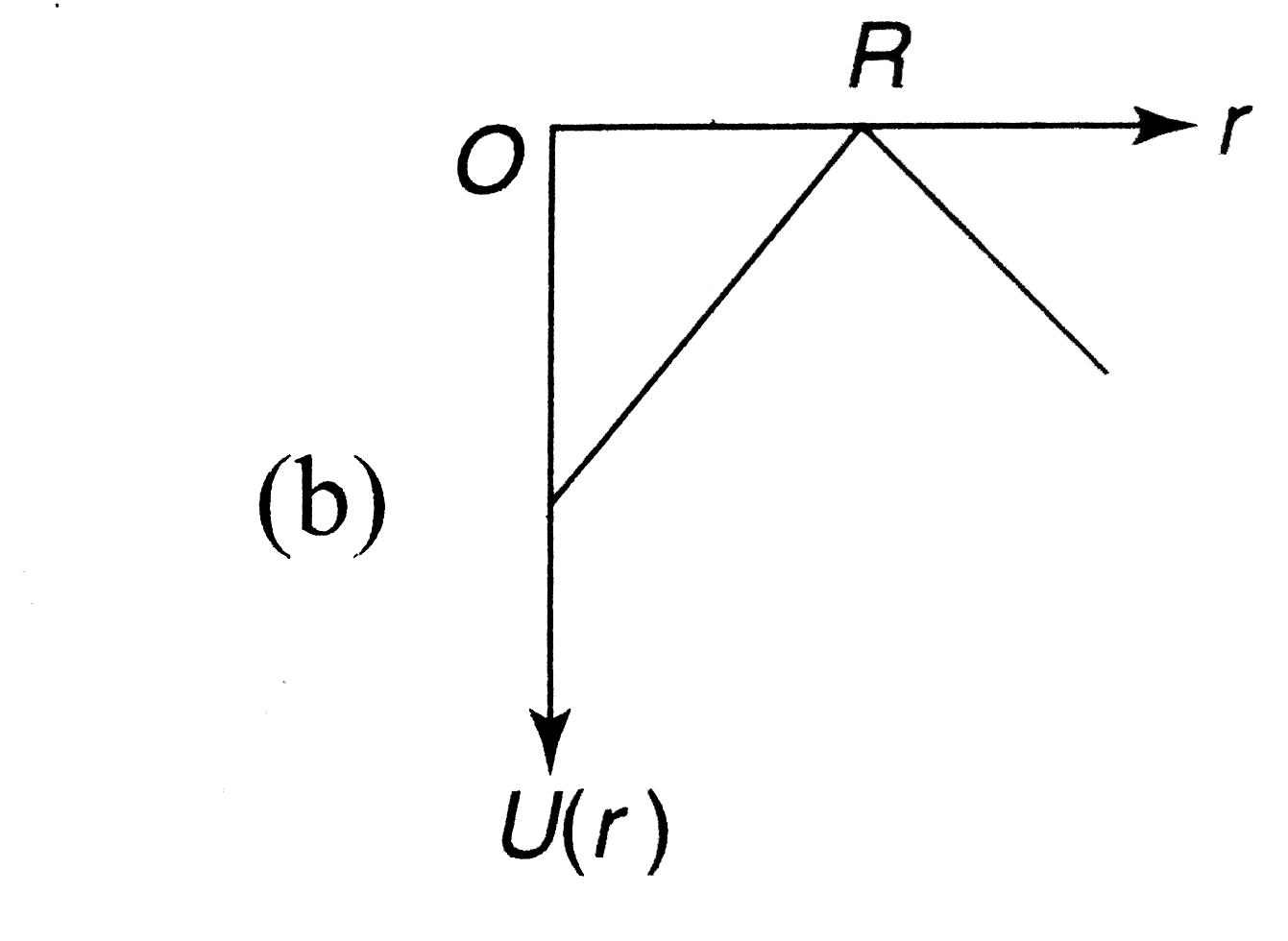 C
C D
D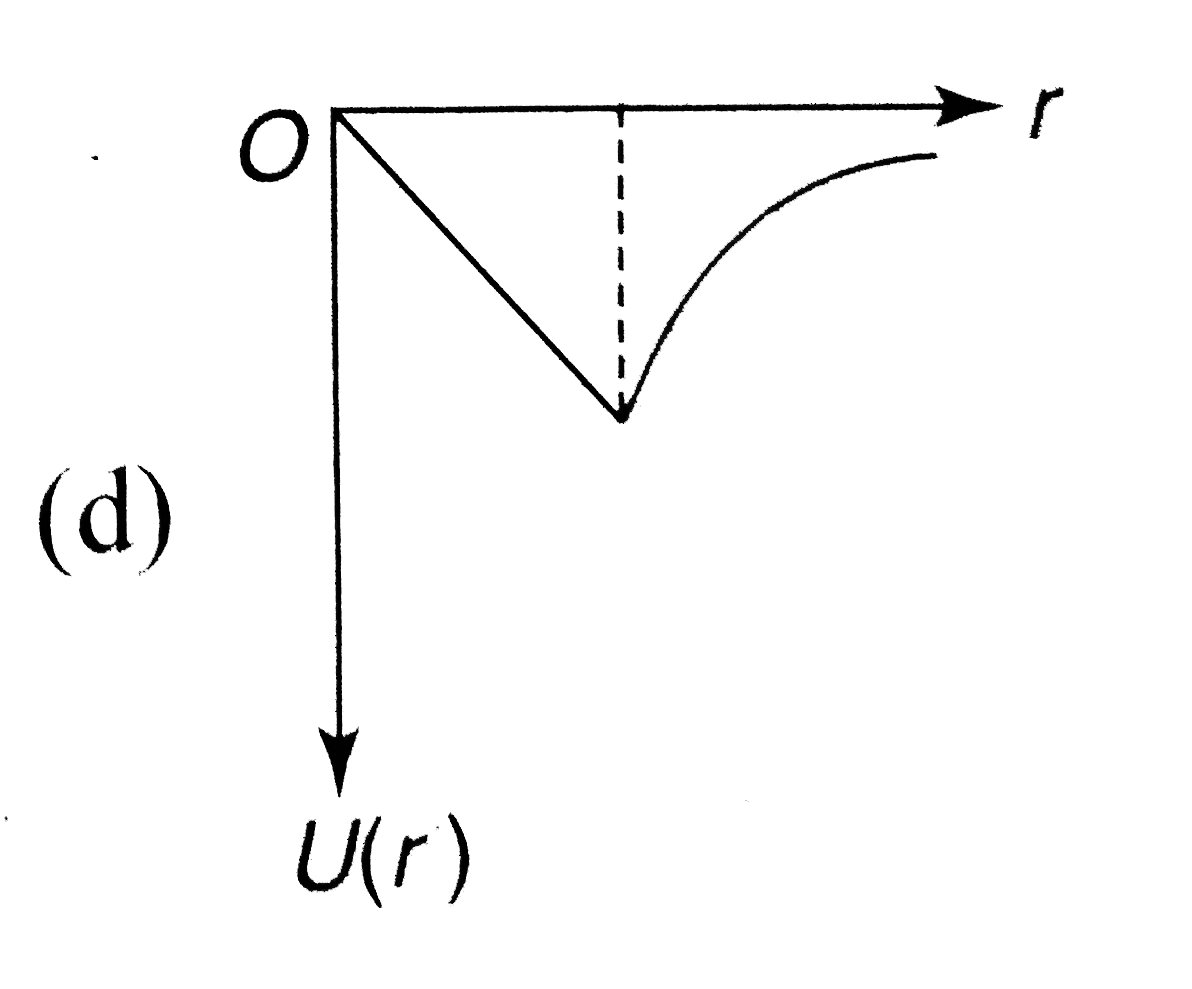
The M.I. of solid sphere of mass M and radius R about its diameter is
A25MR2B75MR2C23MR2D53MR2A shell of mass M and radius R has another point mass m placed at a distance r from its centre (r>R). The force of attraction between the shell and point mass is :
AF=GMmrBF=GMmr2Cf=ZeroDNone of these
Find the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
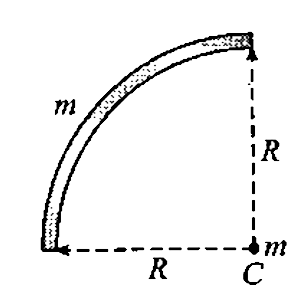
View SolutionA solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.

View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA solid sphere of mass M and radius R spins about an axis passing through its centre making 600 rpm. Its kinetic energy of rotation is
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View Solution
