A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
Gmm'(2r−x)2r3
Gmm'(x−r)2r3
Gmm'(x−r)r3
Gmm'(2x−r)r3
The correct Answer is:C
When 2r<x<2R 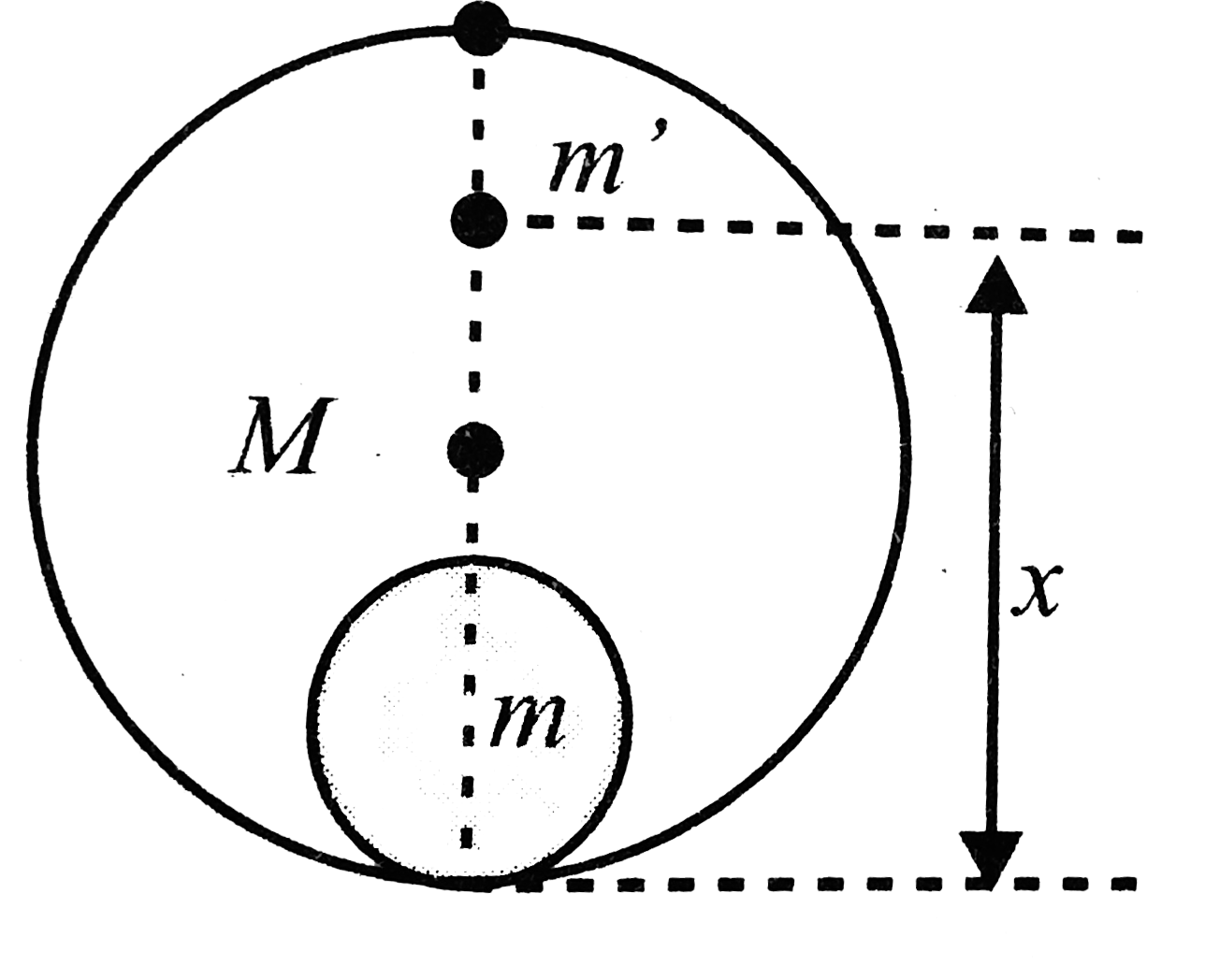
then the force will be due to sphere only.
F=Gmm'(x−r)2
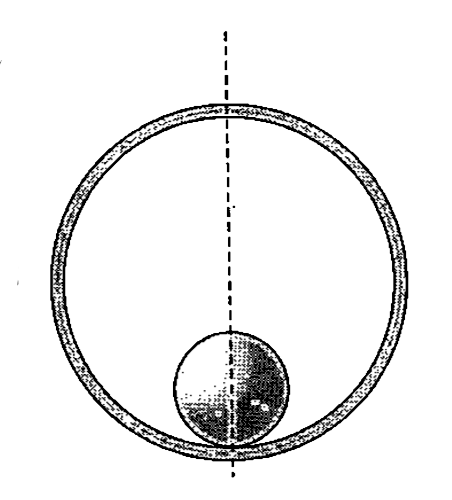
When x>2R. 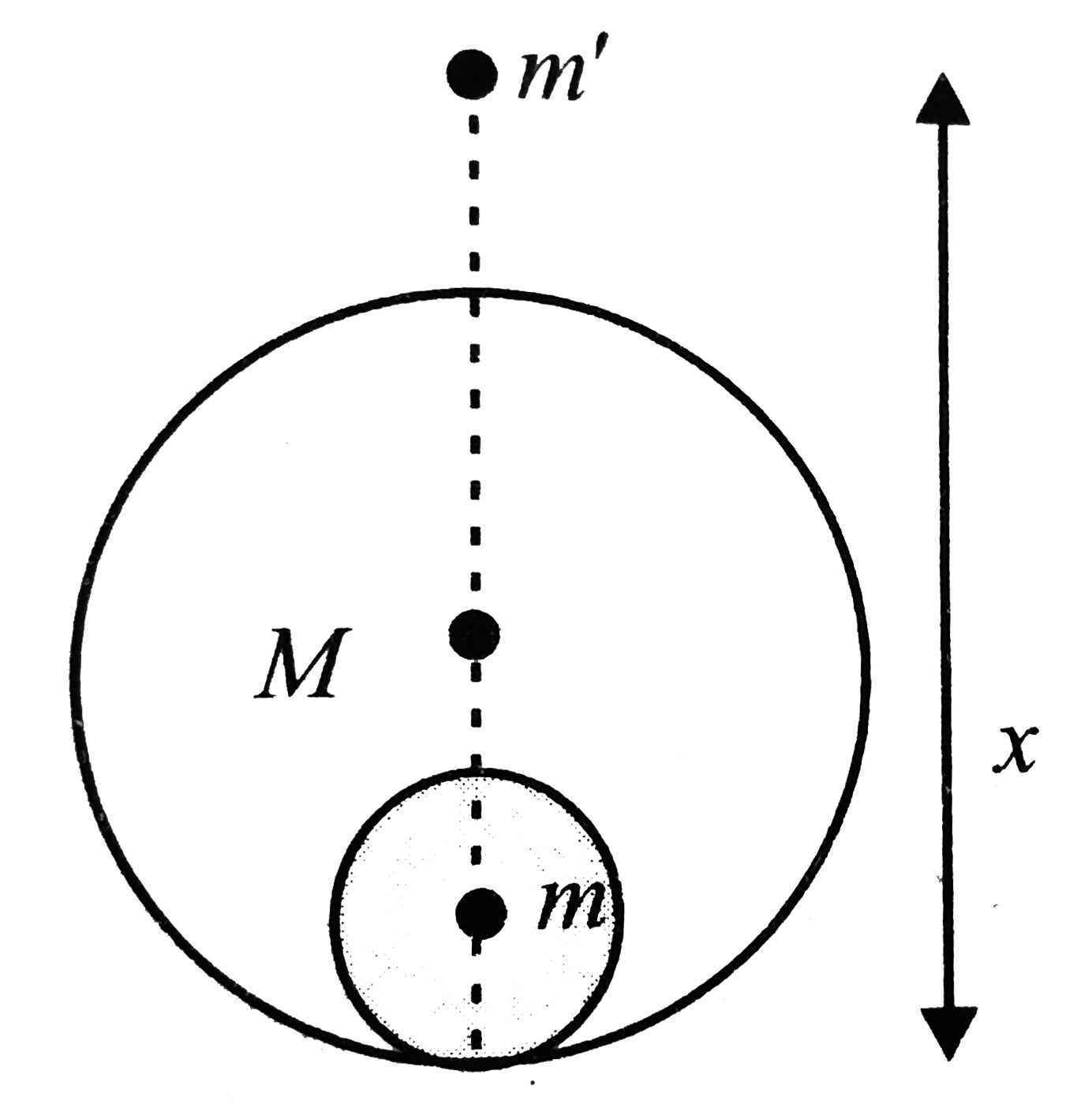
the sphere and the shell both will contribute to the
fsphere=GMm'(x−r)2
Fshell=GMm'(x−R)2
F=GMm'(x−R)2+GMm'(x−r)2
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Integer
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Fill In The Blanks
5 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
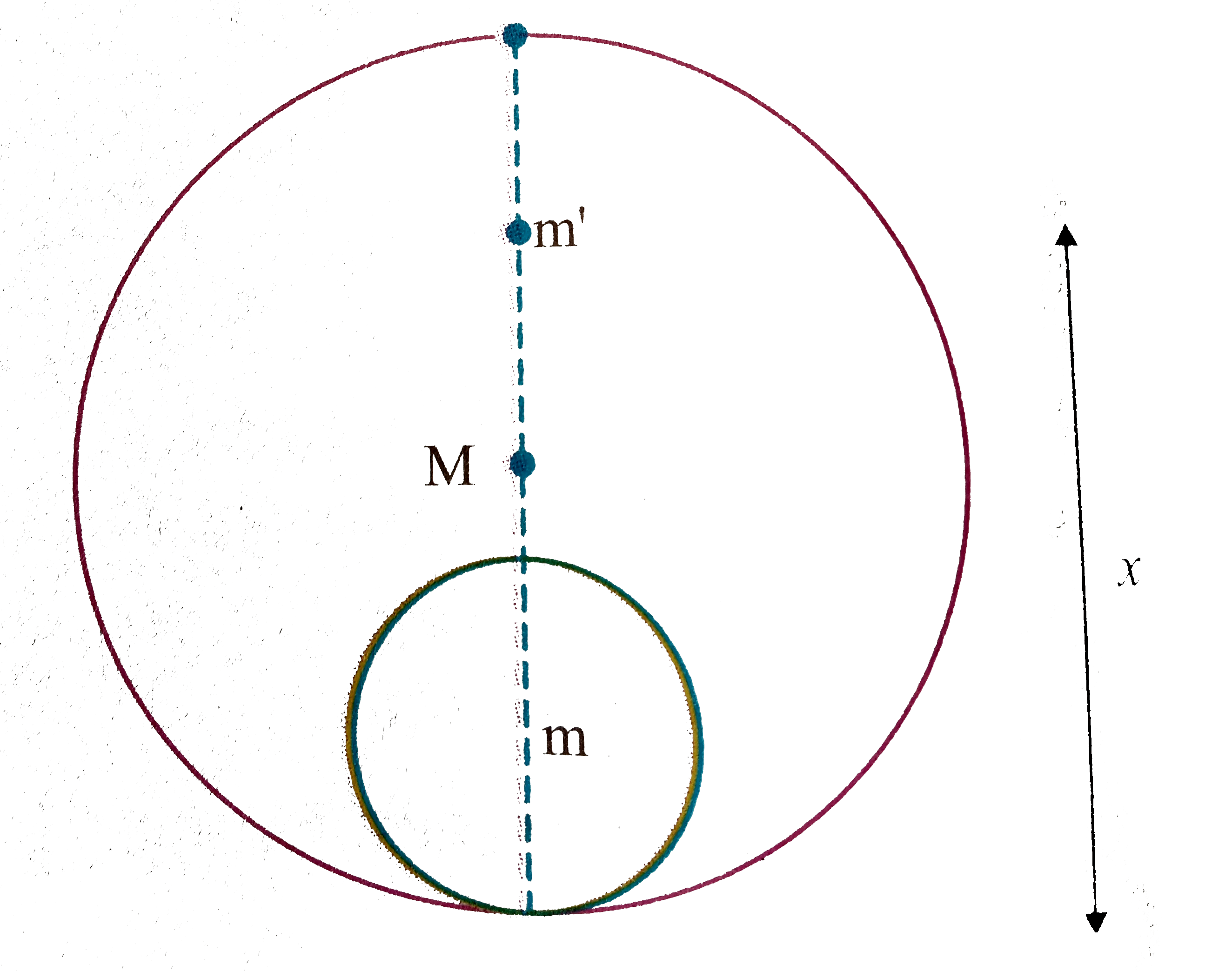
A solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
View Solutiona solid sphere of mass m and radius r is plced nside as hollow thin spherical shell of mass and M and radius R as shown in figure. A particle of mas m is placed on tehline joining the tow centres ast a distance x from the point of contct of th sphere and teh shell. Findn teh mgnitude fo the resultant gravitational force on this particle due to the sphere and the shell if a. r<x<2r,b.2r<x<2Randc.x>2R.

View Solution
Knowledge Check
A solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
2r<x<2RAGmm'4(x−r)2BGmm'(x−r)2CGmm'(x−r)3D2Gmm'(x−r)2A solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2RA2GMm'(x−r)2+Gmm'(x+r)2BGMm'2(x−R)2+2Gmm'(x−r)2CGMm'2(x−r)2+2GMm'(x+r)2DGMm'(x−R)2+Gmm'(x−r)2A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
Athe particle will execute S.H.M inside the shellBthe particle will oscillate inside the shell, but the oscillations are not simple harmonicCthe particle will not oscillate, but the speed the particle will go on increasingDnone ot these
A solid shere of mass m and radius r is placed inside a hollow spherical shell of mass 4m and radius 4r find gravitational field intensity at
(a) r<y<2r (b) 2r<y<8r (c) y>8r
here coordinate is measured from the point of contact of the sphere and the shell
 .
.
View SolutionConsider a thin spherical shell of uniform density of mass M and radius R:
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
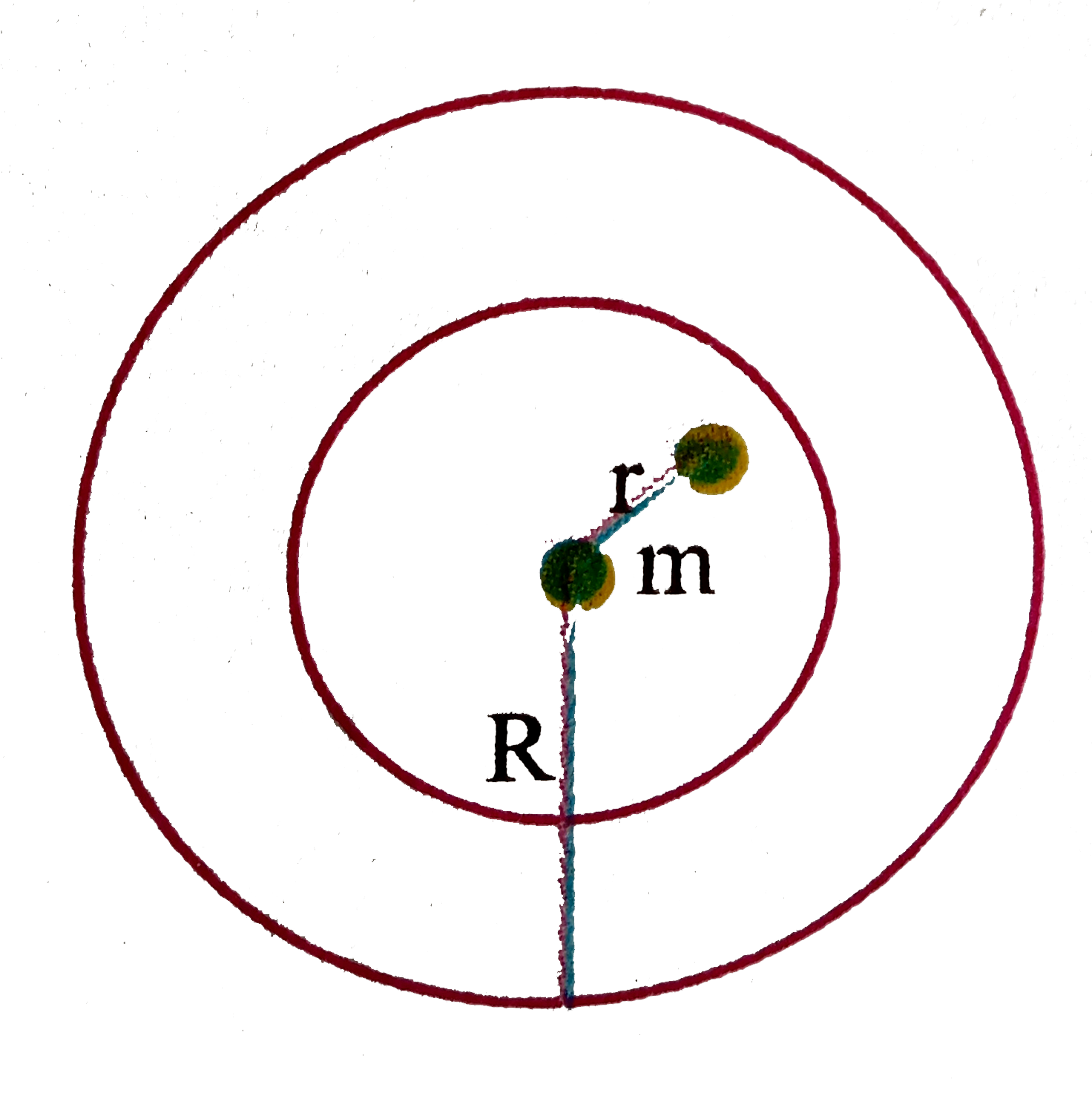
View SolutionA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
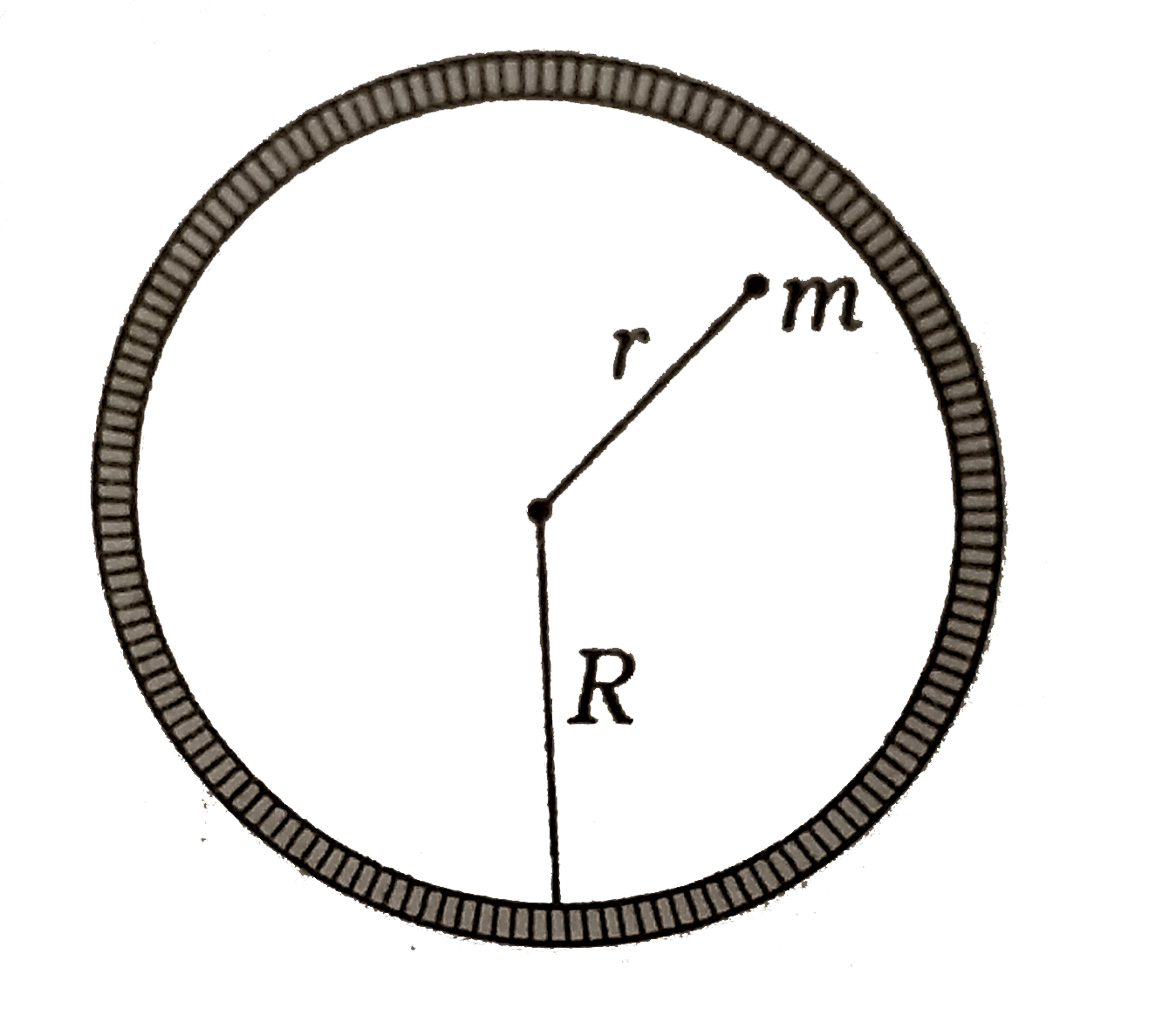
View SolutionA mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
View Solution
