A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

Let at instant, extension of spring is x, v is speed of centre of mass and ω is angular speed of cylinder

Energy of system
E=12mv2+12lω2+12kx2
=12mv2+12⋅25mR2(vR)2+12kx2
=710mv2+12kx2
As total energy is constant
dEdt=0
0=710m⋅2vdvdt+12k2xdxdx
=75mva+kx2v
a=−57kmx=−ω2x
T=2π√7m5k
Topper's Solved these Questions
Similar Questions
A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.
 View Solution
View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
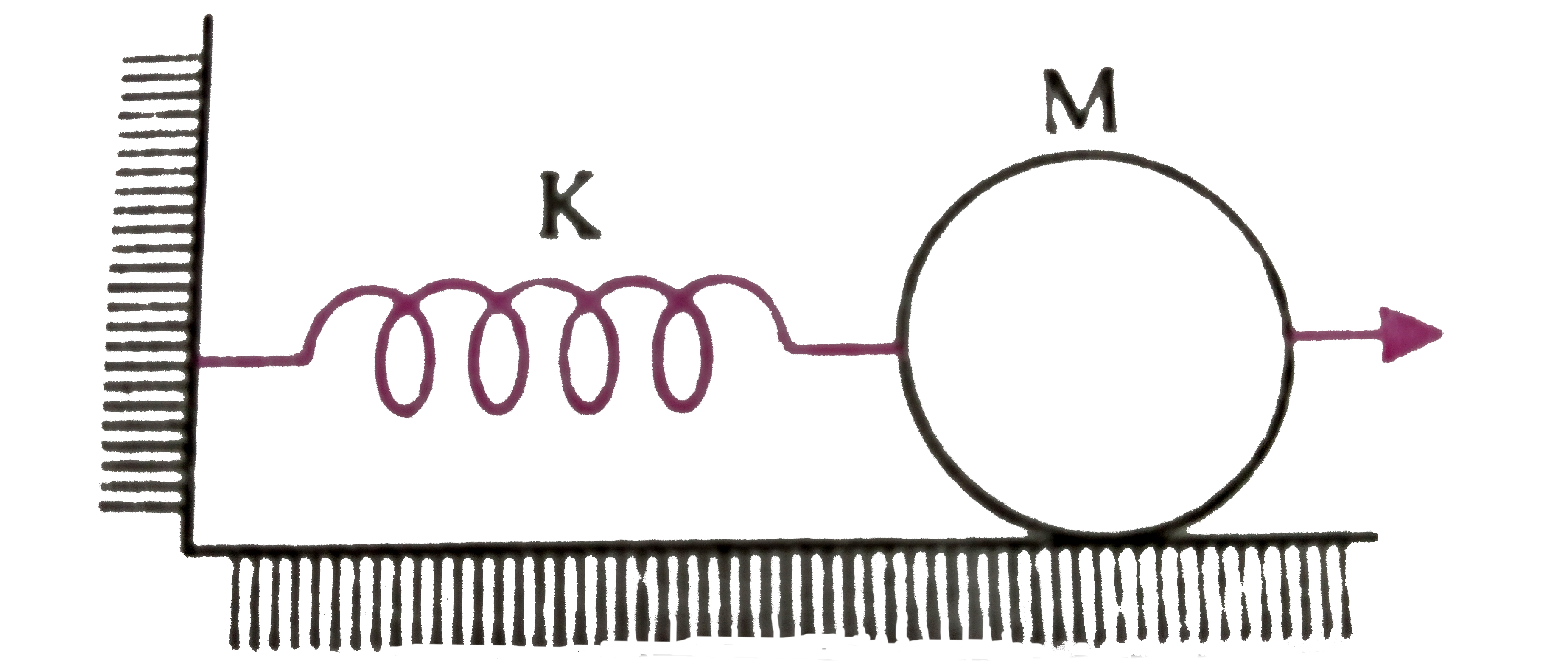 A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A2π√MKB2π√3MKC2π√M2KD2π√3M2K - Question 2 - Select One
A solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) A2π√MkB2π√3m2kC2π√M2kD2π√2M3k
A2π√MkB2π√3m2kC2π√M2kD2π√2M3k - Question 3 - Select One
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.
A spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
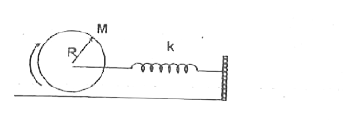
View SolutionA solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.
 View Solution
View SolutionWhen a hollow sphere is rolling without slipping on a rough horizontal surface then the percentage of its total K.E. which is translational is
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View SolutionA solid sphere of mass 1 kg and radius 10 cm rolls without slipping on a horizontal surface, with a velocity of 20 cm/s. The total kinetic energy of the sphere is
View Solution

