A solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

75μmg
47μmg
57μmg
72μmg
The correct Answer is:D
As sphere is rolling we can apply torque equation about point oif contact (about P).
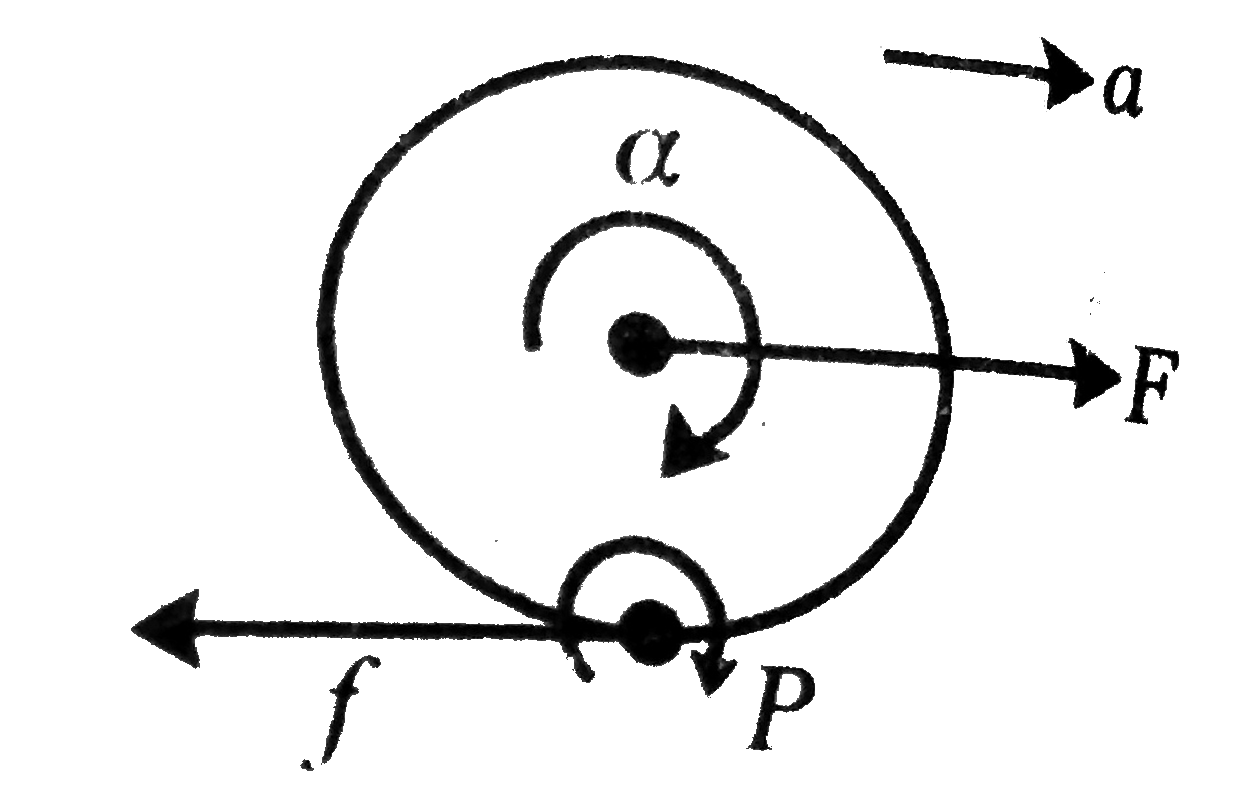
FR=IPα
⇒FR=(75MR2)α
⇒Rα=5F7M=a (acceleration of cm)
Equation of translatory motion
F−f=Ma⇒f=27F.........i
For no sliding f≤μmg⇒F=72μmg
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A solid sphere of mass 2kg is pulled by a constant force acting at its centre on a rough surface having co-efficient of friciton 0.5. The maximum value of F so that the sphere rolls without slipping is

View SolutionA horizontal force F acts on the sphere at its centre as shown. Coefficient of friction between ground and sphere is μ. What is maximum value of F for which there is no slipping?
View Solution
Knowledge Check
A solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to
 A75μmgB47μmgC57μmgD72μmg
A75μmgB47μmgC57μmgD72μmgA mass m rests under the action of a force F as shown in the figure-2.158 on a horizontal surface. The coefficient of friction between the mass and the surface is μ. The force of friction between the mass and the surface is :
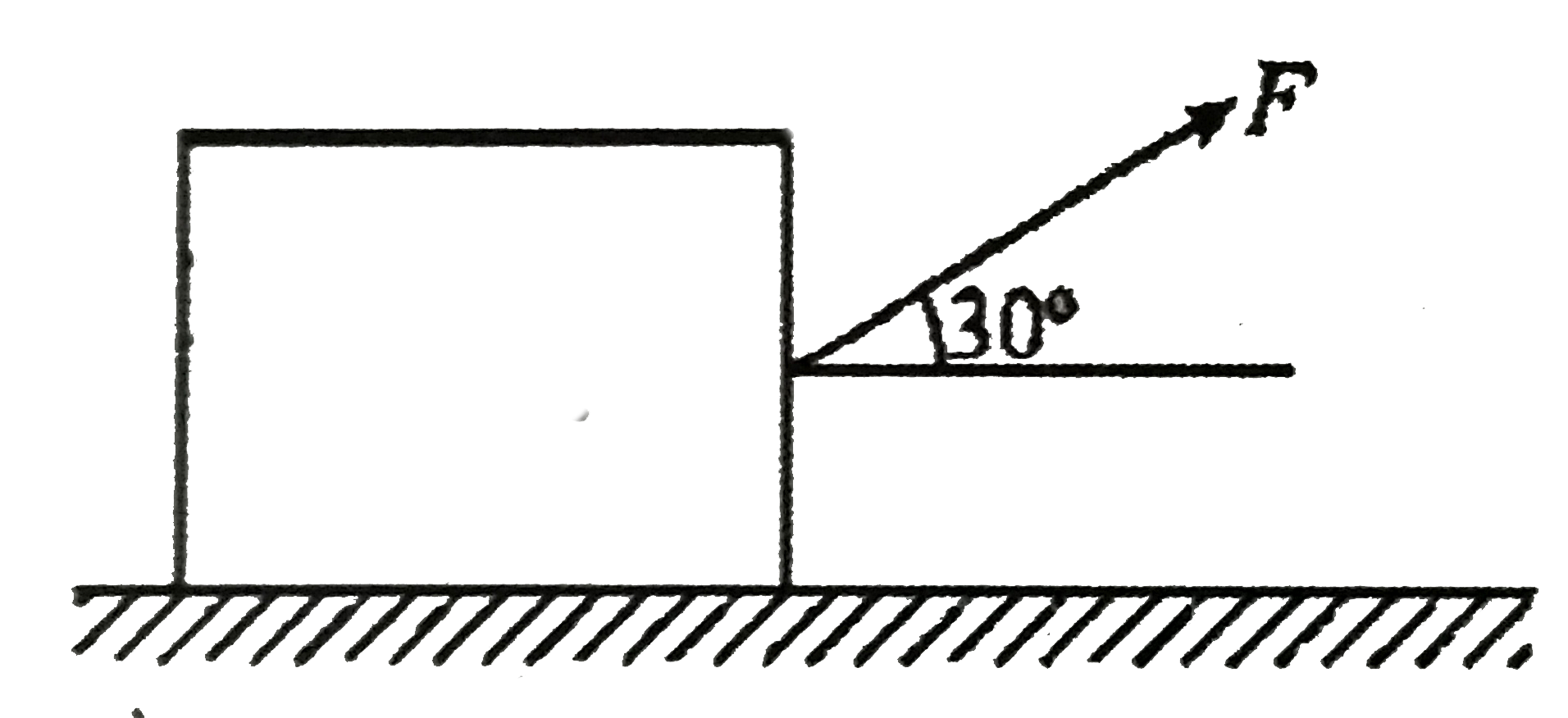 AμmgBμ[mg+F2]CF√32Dμ[mg−F2]
AμmgBμ[mg+F2]CF√32Dμ[mg−F2]A solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is
 A2R5B5R2C7R5D9R5
A2R5B5R2C7R5D9R5
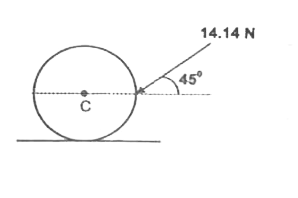
A uniform sphere of mass 20kg and radius 10cm is placed on a rough horizontal surface . The coefficient of friction between the sphere and the surface is 0.5.If a force of magnitude 14.14 N is applied on the sphere at an angle of 45∘ with horizontal as shown in the figure, calculate
(a) frictional force
(b) acceleration of the sphere
(c ) angular acceleration of the sphere
View SolutionA solid sphere of mass 3kg is kept on a horizontal surface. The coefficient of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface? (in N)
View SolutionA solid sphere of masss 0.50 kg si kept on a horizontal surface. The coeffici8ent of static friction between the surfaces in contact is 2/7. What maximum force can be applied at the highest point in the horizontal direction so that the sphere does not slip on the surface?
View SolutionFigure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
If the coefficient of friction between the block and wedge is μ, and the block comes to rest with respect to wedge at a point E on the rough surface then BE will be
View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution
