A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
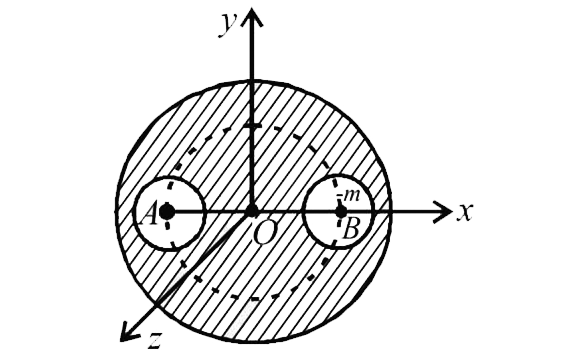
The gravitational force due to this object at the origin is zero.
the gravitational force at the point B(2,0,0) is zero.
the gravitational potential is the same at all points of circle y2+z2=36
the gravitational potential is the same at all points on the circle y2+z2=4.
The correct Answer is:A, C, D
(a,c,d) The gravitational field intensity at the point O is zero
(as the cavities are symmetrical with respect to O.) Now the
force acting on a test mass m0 placed at O is given by
F=m0E=m0×0=0
Now, Y2+z2=36 represents the equation of a circle with
centre (0,0,0) and radius 6 units the plane of the circle is
perpendicular to x-axis.
Topper's Solved these Questions
Similar Questions
A solid sphere of uniform density and radius 4 units is located with its centre at the origin O of coordinates. Two sphere of equal radii 1 unit, with their centres at A(-2,0 ,0) and B(2,0,0) respectively, are taken out of the solid leaving behind spherical cavities as shown if fig Then:
View SolutionA nonconducting sphere of radius R=5cm has its center at the origin O of the coordinate system as shown in (Fig. 3.112). It has two spherical cavities of radius r=1cm, whose centers are at 0,3cm and 0,−3cm, respectively, and solid material of the sphere has uniform positive charge density ρ=1/πμCm−3. Calculate the electric potential at point P(4cm,0).
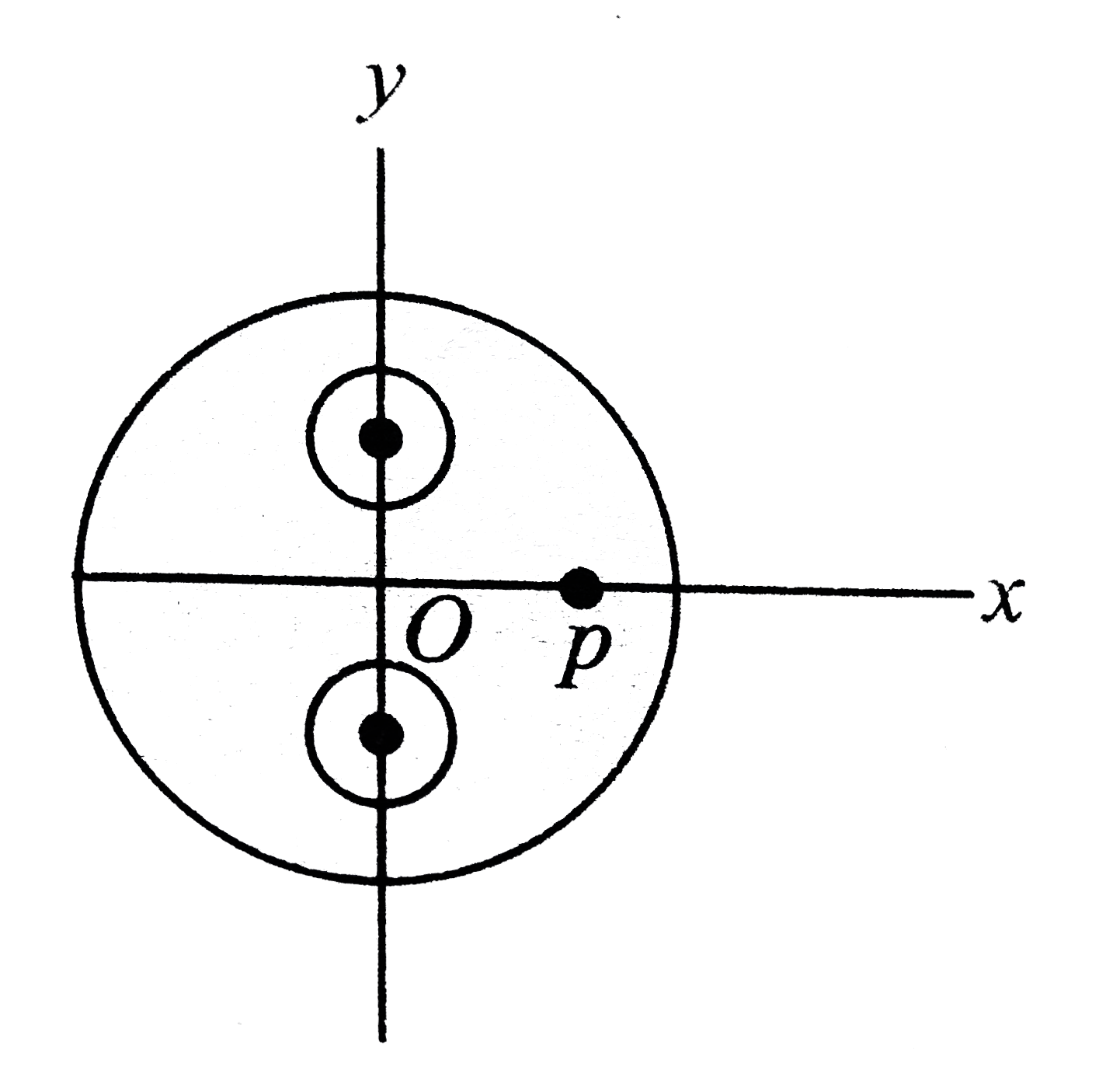.View Solution
Knowledge Check
- Question 1 - Select One
Consider a solid sphere of density ρ and radius 4R. Centre of the sphere is at origin. Two spherical cavities centred at (2R,0) and (−2R,0) are created in sphere. Radii of both cavities is R. In left cavity material of density 2ρ is filled while second cavity is kept empty. What is gravitational field at origin.
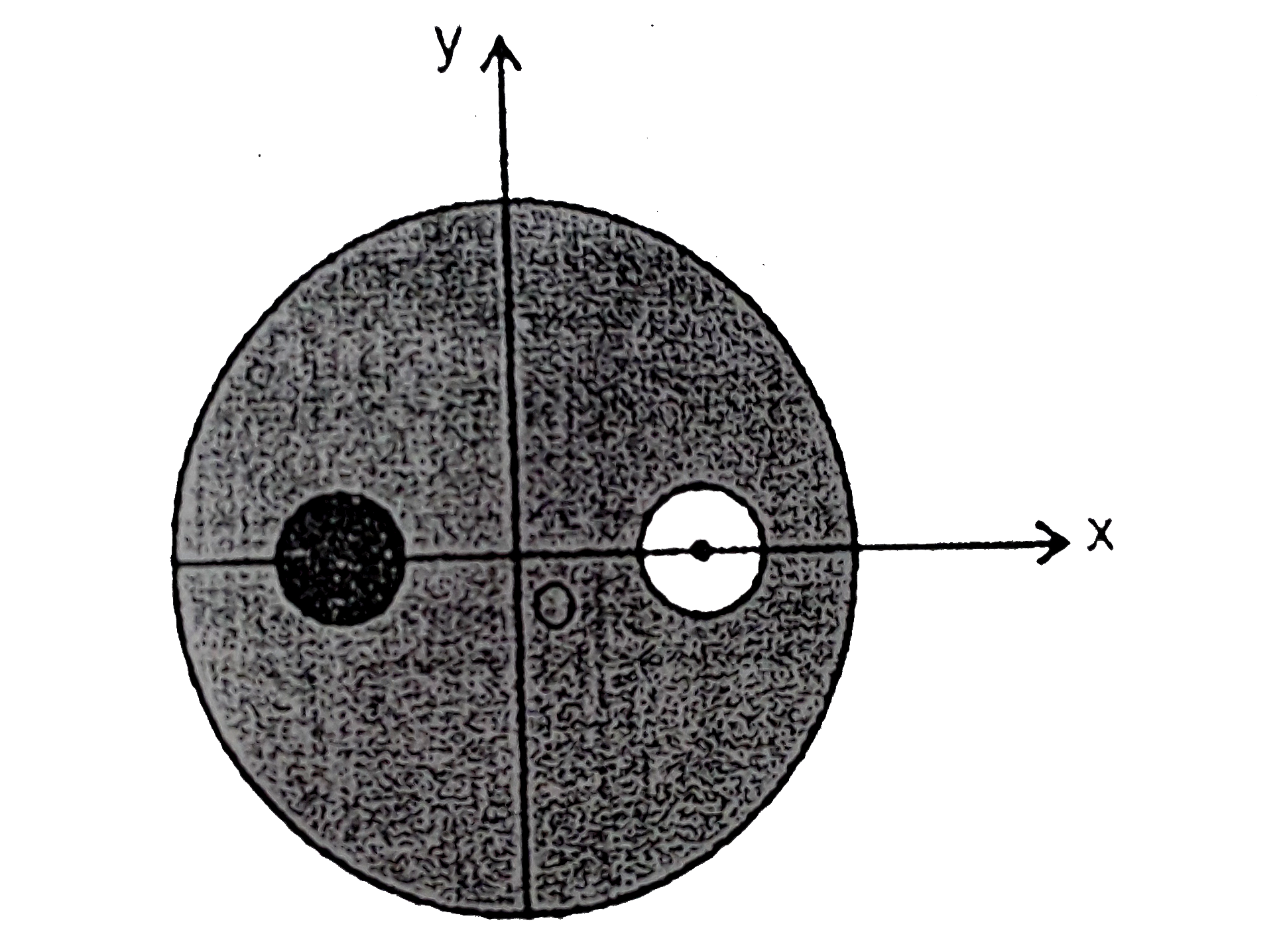A4GρπR3B3GρπR2CGρπR3D2GρπR3 - Question 2 - Select One
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in given figure. The sphere with cavity now applies a gravitational force F2 on same particle placed at P. The ratio F2/F1 will be
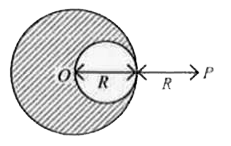A1/2B7/9C3D7 - Question 3 - Select One
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
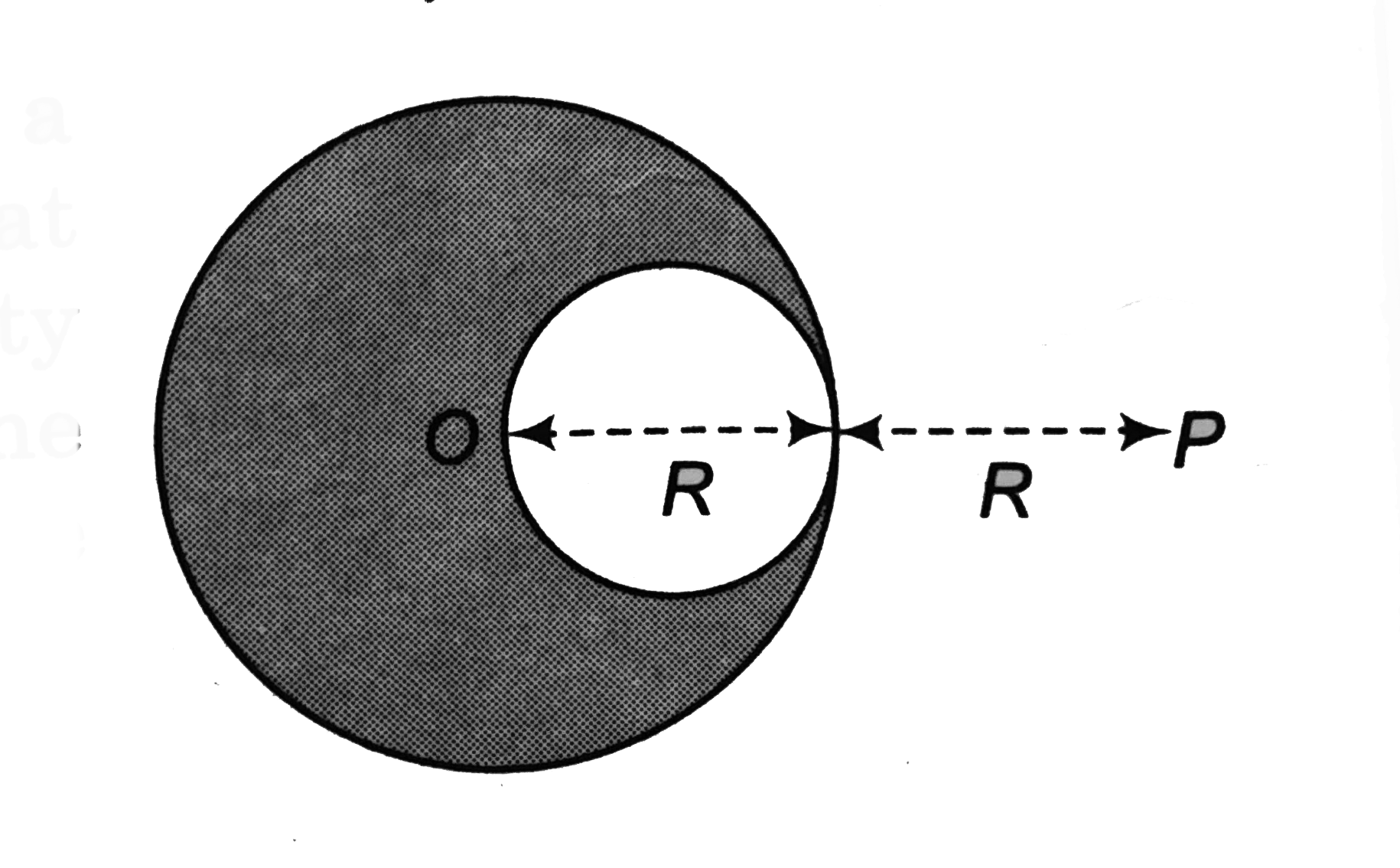A12B79C3D7
A solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?
View SolutionCalculate the void space in closest packing of n spheres of radius 1 unit, n spheres of radiys 0.414 units, and 2n spheres of radius 0.225 units.
View SolutionTwo charges of magnirude −2Qand+Q are located at points (a,0)and(4a,0) respectively .
What is the electric flux due to charges through a sphere of radius '3a' with its center at the origin.View SolutionA solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
View Solution