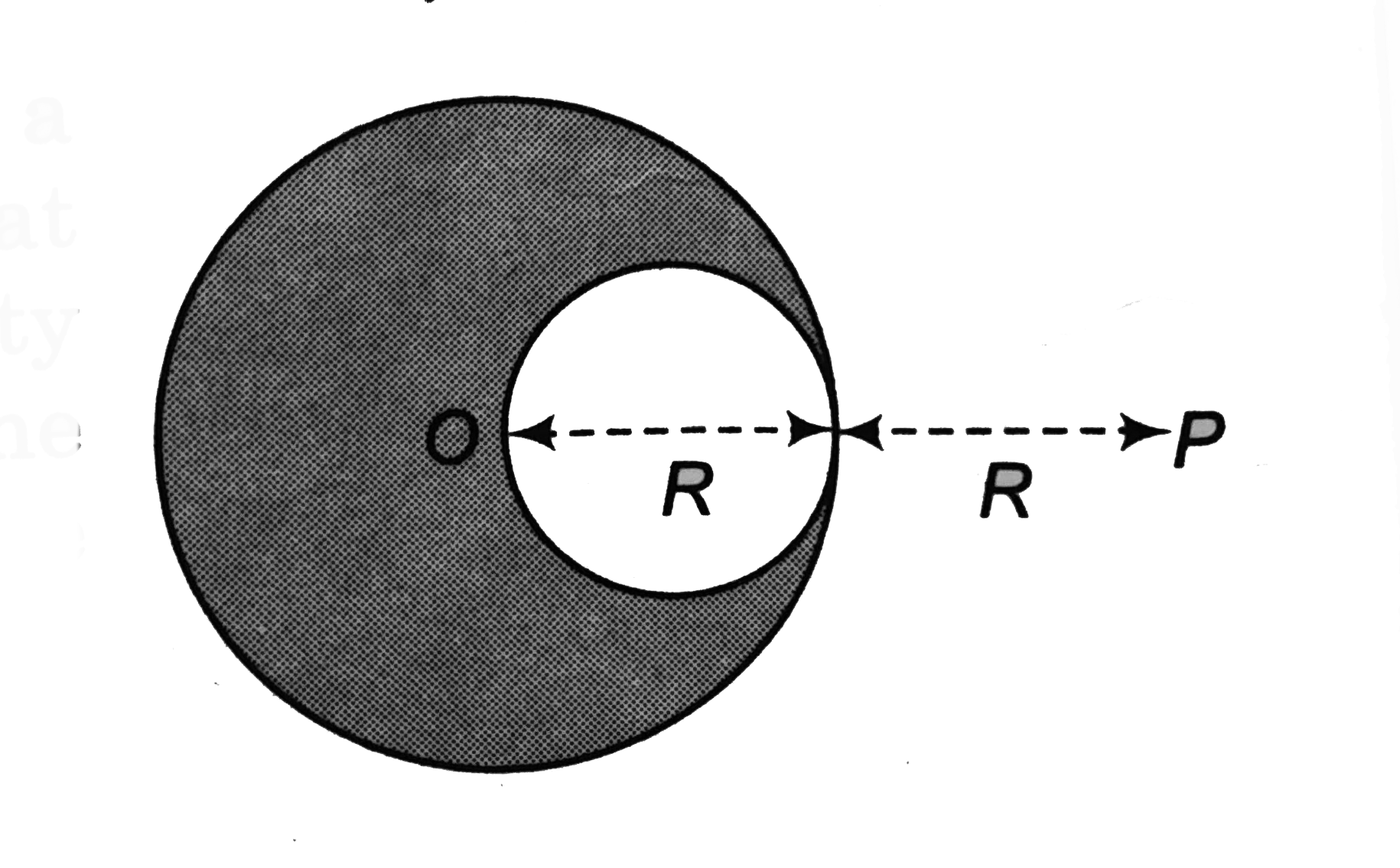
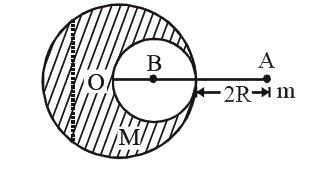
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
1/2
7/9
3
7
The correct Answer is:B
Step by step video, text & image solution for A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F_(1) on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R//2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F_(2) on same particle placed at P. The radio F_(2)//F_(1) will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 3
50 Videos
- PRACTICE PAPERSBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPERSEXERCISE - Practice Paper 3
50 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTIPSCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
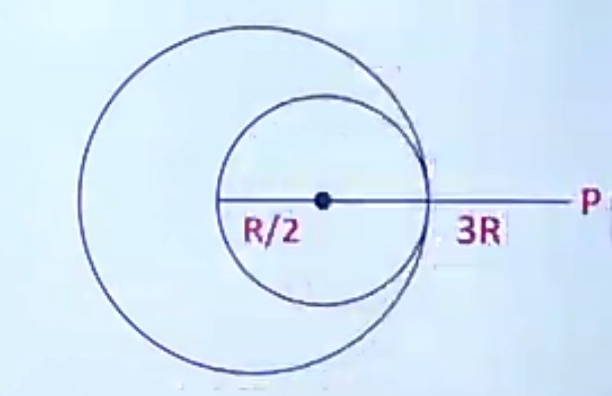
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
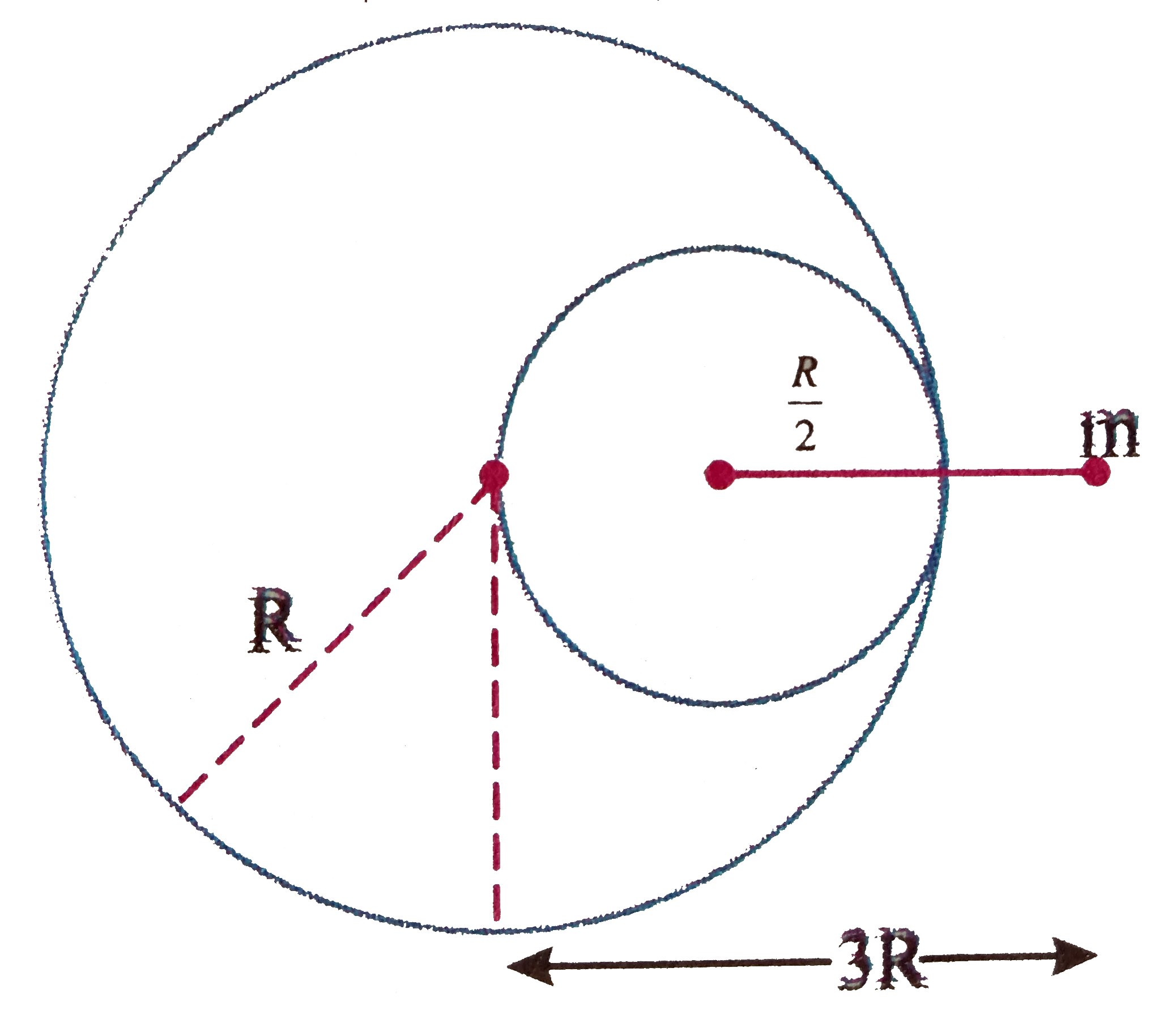
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
View Solution
Knowledge Check
A solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 A1/2B7/9C3D7
A1/2B7/9C3D7A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in given figure. The sphere with cavity now applies a gravitational force F2 on same particle placed at P. The ratio F2/F1 will be
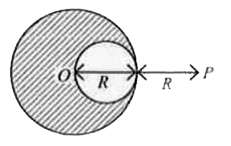 A1/2B7/9C3D7
A1/2B7/9C3D7A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 A12B79C3D7
A12B79C3D7
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

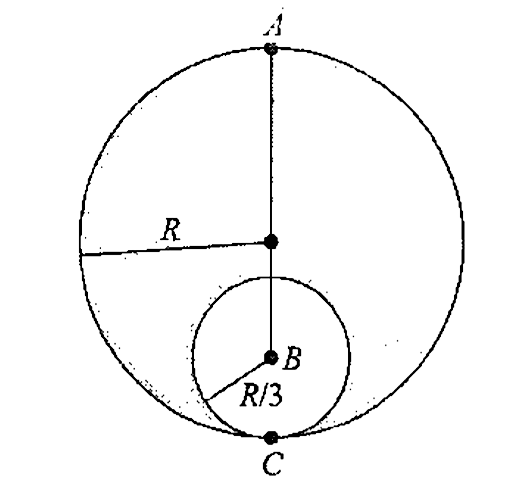
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
View SolutionA solid sphere of radius R gravitationally attracts a particle placed at 3R form its centre with a force F1. Now a spherical cavity of radius (R2) is made in the sphere (as shown in figure) and the force becomes F2 The value of F1:F2 is:
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View Solution
