A solide homogeneous cylinder of height h and base radius r is kept vertically on a conveyer belt moving horizontally with an increasing velocity v=a+bt2. If the cylinder is not allowed to slip then the time whem the cylinder is about to topple , will be equal to
The correct Answer is:(a) μg2b,(b)grbh
dvdt=2bt
μg=2bt
t=μg2b
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:OBJECTIVE QUESTIONS ( only one choice is correct )
Explore 80 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:More than one correct
Explore 18 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
A cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionA uniform cylinder of height h and radius r is placed with its circular face on a rough inclined plane and the inclination of the plane to the horizontal is gradually increased. If μ is the coefficient of friction, then under what condition the cylinder will (a) slide before toppling (b) topple before sliding.
View Solution
Knowledge Check
A cylinder of height H and diameter H/4 is kept on a frictional turntable as shown in Fig. The axis of the cylinder is perpendicular to the surface of the table and the distance of axis of the cylinder is 2H from the centre of the table. The angular speed of the turntable at which the cylinder will start toppling (assume that friction is sufficient to prevent slipping) is
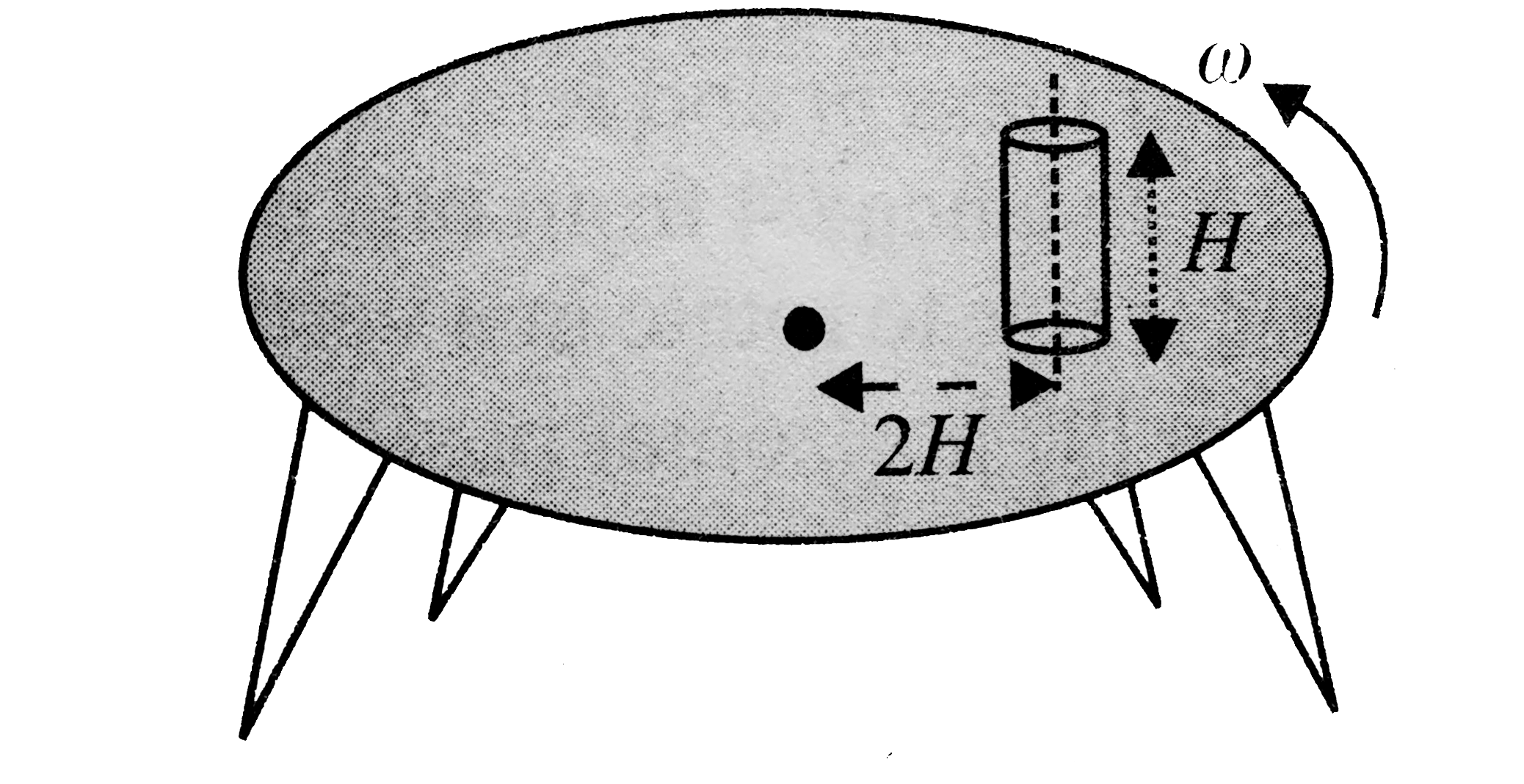 A√g2(12−H)B√g(12−H)C√g4HD√g8H
A√g2(12−H)B√g(12−H)C√g4HD√g8HA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
A2F3MrB3F2MrCF3MrDF2MrA solid cylinder of mass 0.1 kg having radius 0.2m rolls down an inclined plane of height 0.6m without slipping. The linear velocity the cylinder at the bottom of the inclined plane is
A28ms−1B2.8ms−1C280ms−1D0.28ms−1
A cylinder of weight W and raidus R is to be raised onto a horizontal step of height h=R/3 as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of F to raise the cylinder.

View SolutionA cylinder of weight W and raidus R is to be raised onto a horizontal step of height h=R/3 as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of F to raise the cylinder.

View SolutionA solid cylinder of radius m is kept on an inclined plane on its base and it does not slide. The angle of incline plane is 53∘ with horizontal and it is fixed. What will be maxcimum height (in meters) of the cylinder for it not to topple.
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View Solution