A source and an observer is approaching closer with a relative velocity of 40ms−1. If the true frequency of the source is 1200 Hz calculate the observed frequency under these conditions: (i) the source alone is moving (ii) the observer alone is moving. Take velocity of sound in air to be 340ms−1.
The correct Answer is:(i) n'=(V−Vi)n/(V−Vs)=(340−0)1200/340−40=1360H (ii) n'=1200×380/340=1341.2Hz
To solve the problem, we will use the Doppler effect formula for sound. The formula for the observed frequency (f′) when either the source or the observer is moving is given by:
f′=fv+v0v−vs
Where:
- f′ is the observed frequency,
- f is the true frequency of the source,
- v is the speed of sound in air,
- v0 is the speed of the observer (positive if moving towards the source),
- vs is the speed of the source (positive if moving away from the observer).
Part (i): When the source alone is moving
1. Identify the known values:
- True frequency of the source, f=1200Hz
- Speed of sound, v=340m/s
- Speed of the source, vs=40m/s (moving towards the observer)
- Speed of the observer, v0=0m/s (observer is stationary)
2. Substitute the values into the Doppler effect formula:
f′=1200340+0340−40
3. Calculate the denominator:
340−40=300
4. Calculate the observed frequency:
f′=1200340300=1200×1.1333≈1360Hz
Part (ii): When the observer alone is moving
1. Identify the known values:
- True frequency of the source, f=1200Hz
- Speed of sound, v=340m/s
- Speed of the observer, v0=40m/s (moving towards the source)
- Speed of the source, vs=0m/s (source is stationary)
2. Substitute the values into the Doppler effect formula:
f′=1200340+40340−0
3. Calculate the numerator:
340+40=380
4. Calculate the observed frequency:
f′=1200380340=1200×1.1176≈1341.2Hz
Final Answers:
- (i) When the source alone is moving: f′≈1360Hz
- (ii) When the observer alone is moving: f′≈1341.2Hz
- f′ is the observed frequency,
- f is the true frequency of the source,
- v is the speed of sound in air,
- v0 is the speed of the observer (positive if moving towards the source),
- vs is the speed of the source (positive if moving away from the observer).
- True frequency of the source, f=1200Hz
- Speed of sound, v=340m/s
- Speed of the source, vs=40m/s (moving towards the observer)
- Speed of the observer, v0=0m/s (observer is stationary)
f′=1200340+0340−40
340−40=300
f′=1200340300=1200×1.1333≈1360Hz
- True frequency of the source, f=1200Hz
- Speed of sound, v=340m/s
- Speed of the observer, v0=40m/s (moving towards the source)
- Speed of the source, vs=0m/s (source is stationary)
f′=1200340+40340−0
340+40=380
f′=1200380340=1200×1.1176≈1341.2Hz
- (i) When the source alone is moving: f′≈1360Hz
- (ii) When the observer alone is moving: f′≈1341.2Hz
Topper's Solved these Questions
Similar Questions
A source of sound S is moving with a velocity of 50m/s towards a stationary observer. The observer measures the frequency of the source as 1000 Hz. What will be the apparent frequency of the source as 1000 Hz. What will be the apparent frequency of the source when it is moving away from the observer after crossing him? The velocity of the sound in the medium is 350m/s
View SolutionA source of sound S is moving with a velocity of 50m/s towards a stationary observer. The observer measures the frequency of the source as 1000 Hz. What will be the apparent frequency of the source as 1000 Hz. What will be the apparent frequency of the source when it is moving away from the observer after crossing him? The velocity of the sound in the medium is 350m/s
View SolutionA source of sound and an observer are approaching each other with the same speed, which is equal to (110) times the speed of sound. The apparent relative change in frequency of source is
View SolutionA source of sound attached to the bob of a simple pendulum execute SHM the difference between the apparent frequency of sound as received by an observer during its approach and recession at the mean position of the SHM motion is 2% of the natural frequency of the source the velocity of the source at the mean position is (velocity of sound in the air is 340m/s) [Assume velocity of sound source ≤≤ velocity of sound in air]
View SolutionWhen the observer moves towards the stationary source with velocity, v1, the apparent frequency of emitted note is f1. When the observer moves away from the source with velocity v1, the apparent frequency is f2. If v is the velocity of sound in air and f1f2 = 2,then vv1 = ?
View Solutionwhen a source is going away from a stationary observer with the velocity equal to that of sound in air , then the frequency heard by observer is n times the original frequency . The value of n is
View SolutionIf source and observer both are relatively at rest and if speed of sound is increased then frequency heard by observer will
View SolutionThere is a source of sound (a tuning fork) moving towards a reflecting wall will a speed of 30ms−1. The velocity of the sound in air is 330ms−1and the frequency of the tuning fork is 600 Hz. The observer is between the source and the wall and is moving with some velocity V1 towards the wall. The beat frequency heard by the observer is 4 Hz. If the tuning fork is waxed, the frequency beats heard by the observer becomes 3 Hz. If the new frequency of tuning fork is k then k/50 is
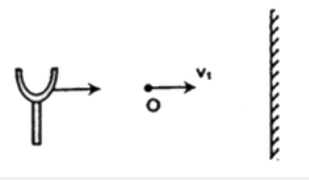 View Solution
View SolutionAn observer travelling with a constant velocity of 16.5ms−1, passes closes to a stationary source of sound and notices that there is a change of frequency of 50 Hz as he passes the source. Calculate the frequency of the source. (Speed of sound in air = 330 ms−1).
View SolutionThe source (S) of sound is moving constant velocity v0 as shown in diagram. An observer O listens to the sound emmited by the source. The observed frequency of the sound
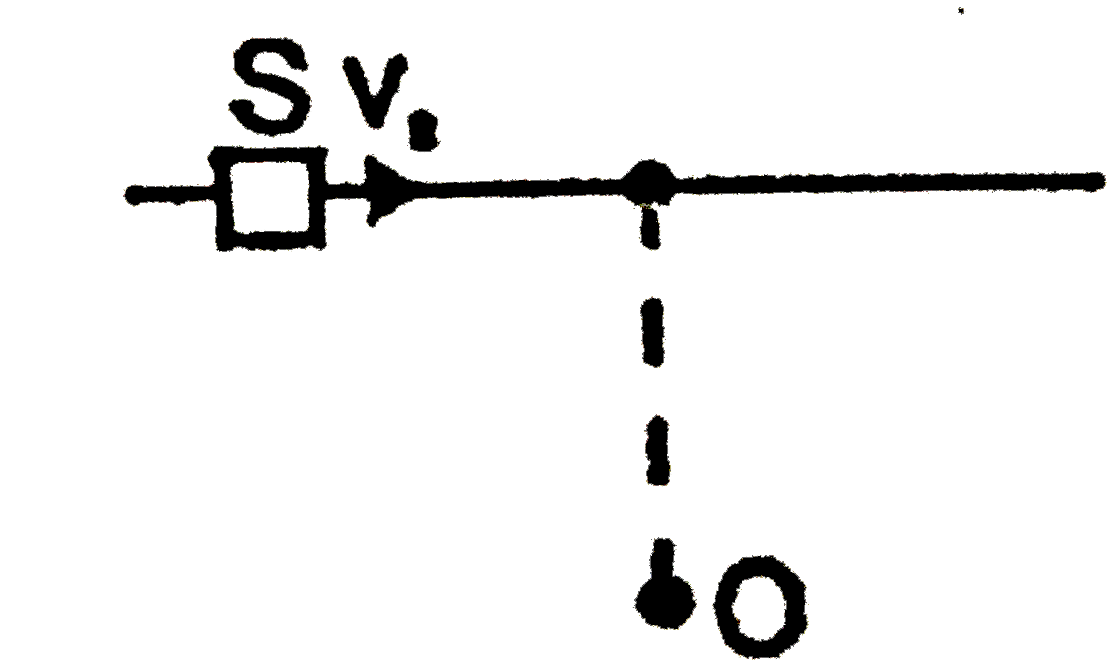 View Solution
View Solution

