A source S1 is producing 1015 photons per second of wavelength 5000Ã…. Another source S2 is producing 1.02×1015
wavelength 5100 A Then, (Power ofS2)/(Power ofS1) is equal to
1.00
1.02
1.04
0.98
The correct Answer is:A
To find the ratio of the power of two sources S1 and S2, we can follow these steps:
Step 1: Write down the given data
- For source S1:
- Number of photons per second, n1=1015
- Wavelength, λ1=5000Å=5000×10−10m
- For source S2:
- Number of photons per second, n2=1.02×1015
- Wavelength, λ2=5100Å=5100×10−10m
Step 2: Calculate the energy of a single photon for each source
The energy of a photon is given by the formula:
E=hcλ
where:
- h is Planck's constant (6.626×10−34Js)
- c is the speed of light (3×108m/s)
For source S1:
E1=hcλ1=(6.626×10−34)(3×108)5000×10−10
For source S2:
E2=hcλ2=(6.626×10−34)(3×108)5100×10−10
Step 3: Calculate the total power for each source
The power produced by each source can be calculated as:
P=n⋅E
Thus, for source S1:
P1=n1⋅E1=n1⋅hcλ1
And for source S2:
P2=n2⋅E2=n2⋅hcλ2
Step 4: Find the ratio of the powers
To find the ratio of the powers P2P1:
P2P1=n2⋅E2n1⋅E1=n2⋅hcλ2n1⋅hcλ1=n2⋅λ1n1⋅λ2
Step 5: Substitute the values
Now substituting the values we have:
P2P1=(1.02×1015)⋅(5000Å)(1015)⋅(5100Å)
Step 6: Simplify the expression
=1.02⋅50005100
=51005100=1
Final Result
Thus, the ratio of the power of S2 to the power of S1 is:
P2P1=1
- For source S1:
- Number of photons per second, n1=1015
- Wavelength, λ1=5000Å=5000×10−10m
- Number of photons per second, n2=1.02×1015
- Wavelength, λ2=5100Å=5100×10−10m
The energy of a photon is given by the formula:
E=hcλ
where:
- h is Planck's constant (6.626×10−34Js)
- c is the speed of light (3×108m/s)
E1=hcλ1=(6.626×10−34)(3×108)5000×10−10
E2=hcλ2=(6.626×10−34)(3×108)5100×10−10
The power produced by each source can be calculated as:
P=n⋅E
Thus, for source S1:
P1=n1⋅E1=n1⋅hcλ1
And for source S2:
P2=n2⋅E2=n2⋅hcλ2
To find the ratio of the powers P2P1:
P2P1=n2⋅E2n1⋅E1=n2⋅hcλ2n1⋅hcλ1=n2⋅λ1n1⋅λ2
Now substituting the values we have:
P2P1=(1.02×1015)⋅(5000Å)(1015)⋅(5100Å)
=1.02⋅50005100
=51005100=1
Thus, the ratio of the power of S2 to the power of S1 is:
P2P1=1
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - WAVE NATURE OF MATTER
37 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - DAVISSON AND GERMER EXPERIMENT
3 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - EINSTEIN S PHOTOELECTRIC EQUATION : ENERGY QUANTUM OF RADIATION
23 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A monochromatic source of light operating at 200W
emits 4×1020 photons per second. Find the wavelength
of the light.
View SolutionWhat is power (in watt) of a light source emitting 7.25×1018 photons per second, while the wavelength of light is 620nm ? (use hc=12400eVÅ)
View SolutionWhat is power (in watt) of a light source emitting 5.25×1018 photons per second, while the wavelength of light is 620nm ? (use hc=12400eVÅ)
View SolutionWhat is power (in watt) of a light source emitting 3.125×1018 photons per second, while the wavelength of light is 620nm ? (use hc=12400eVÅ)
View SolutionWhat is power (in watt) of a light source emitting 4.25×1018 photons per second, while the wavelength of light is 620nm ? (use hc=12400eVÅ)
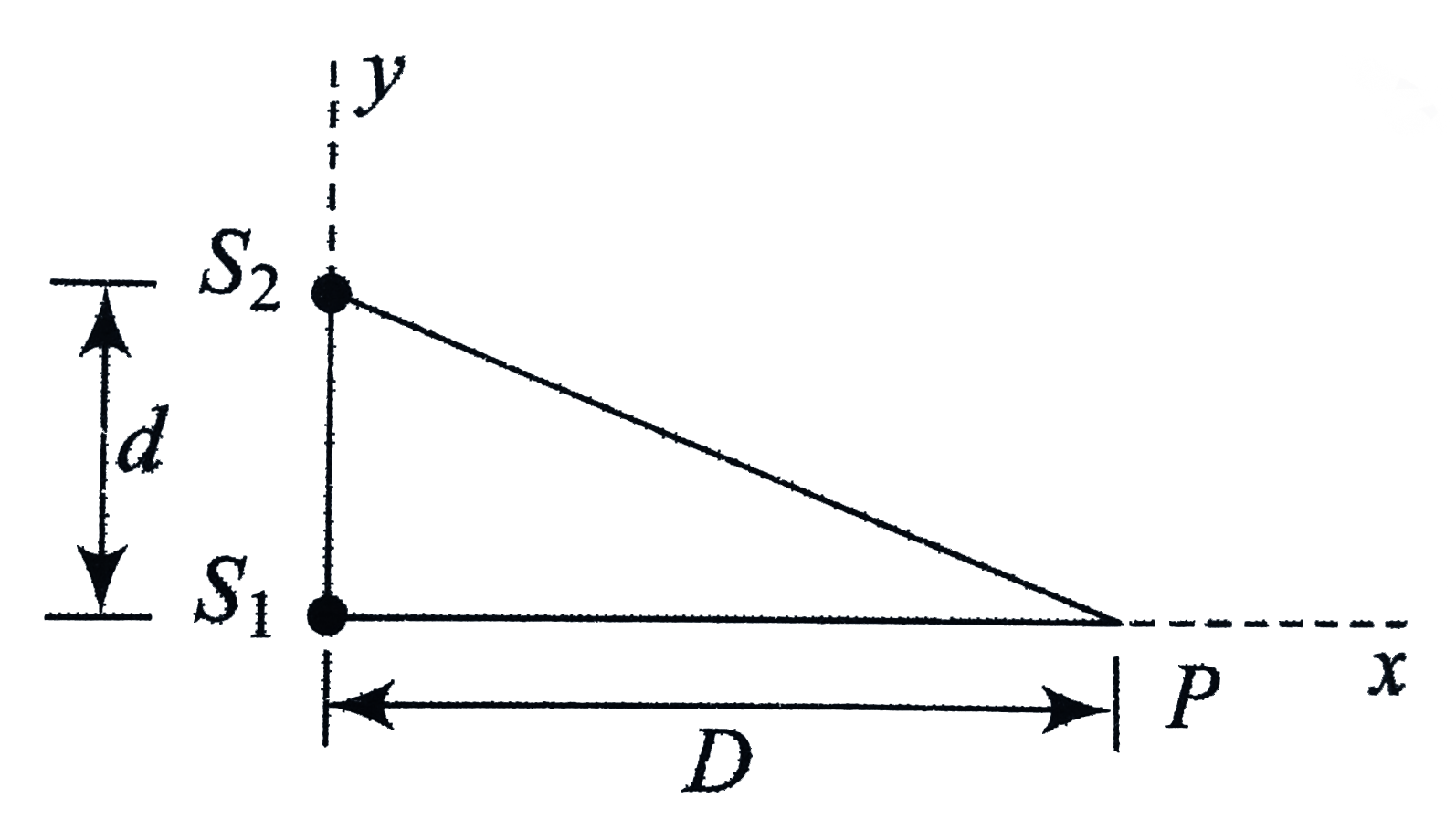
View SolutionTwo sources S1 and S2 emiting light of wavelenght 600 nm placed a distance 1.0×10−2 cm apart.
A detector can be moved on line S1P which is perpendicular to S1S2
(a) What would be the minimum and maximum path difference at the detector as it moves along line S1P ?
(b) Locate the psoition of the farthest minima detected
 .
.
View SolutionCalculate the mass of a photon of sodium light wavelength 600 and velocity 3×108ms−1.
View SolutionThe number of photons emitted per second by a 60 W source of monochromatic light of wavelength 663 nm is:
(h=6.63×10−34Js)
View SolutionTwo identical sources of sound S1andS2 produce intensity I0 at a point P equidistant from each source .
(i) Determine the intensity of each at the point P.
(ii) If the power of S1 is reduced to 64% and phase difference between the two sources is varied continuously , then determine the maximum and minimum intensities at the point P.
(iii) If the power of S1 is reduced by 64% , then determine the maximum and minimum intensities at the point P.
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View Solution
