A sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is
conserved about every point
conserved about the point of contact only
conserved about the centre of the sphere only
conserved about any point on a line parallel to the inclined plane and passing through the centre of the ball
The correct Answer is:D
To determine the angular momentum of a sphere released on a smooth inclined plane, we need to analyze the forces acting on the sphere and the conditions under which angular momentum is conserved.
1. Understanding the System:
- We have a sphere released from the top of a smooth inclined plane. The plane is smooth, meaning there is no friction acting on the sphere.
2. Identifying Forces:
- The forces acting on the sphere are:
- Gravitational force (weight) W=mg acting downwards.
- Normal force N acting perpendicular to the surface of the inclined plane.
3. Torque and Angular Momentum:
- Angular momentum L is conserved when the net torque τ acting on the system is zero.
- Torque is defined as τ=R×F, where R is the position vector from the point about which we are calculating torque to the point of application of the force F.
4. Choosing a Point for Torque Calculation:
- To find where the angular momentum is conserved, we can analyze the torque about different points.
- If we take the center of mass of the sphere as the reference point, the torque due to the gravitational force will be zero because the line of action of the weight passes through the center of mass.
5. Torque Calculation at Different Points:
- If we consider any point along the incline, the gravitational force mg can be resolved into two components:
- mgsinθ (parallel to the incline)
- mgcosθ (perpendicular to the incline)
- The torque due to the normal force N and the component mgcosθ will also be zero at the center of mass since their lines of action pass through this point.
6. Conclusion on Angular Momentum Conservation:
- Since the net torque about the center of mass is zero, the angular momentum of the sphere is conserved as it rolls down the incline.
- However, if we consider points other than the center of mass, the torque due to mgsinθ will not be zero, and thus angular momentum will not be conserved at those points.
Final Answer:
The angular momentum of the sphere is conserved at the center of mass of the sphere as it rolls down the smooth inclined plane.
- We have a sphere released from the top of a smooth inclined plane. The plane is smooth, meaning there is no friction acting on the sphere.
- The forces acting on the sphere are:
- Gravitational force (weight) W=mg acting downwards.
- Normal force N acting perpendicular to the surface of the inclined plane.
- Angular momentum L is conserved when the net torque τ acting on the system is zero.
- Torque is defined as τ=R×F, where R is the position vector from the point about which we are calculating torque to the point of application of the force F.
- To find where the angular momentum is conserved, we can analyze the torque about different points.
- If we take the center of mass of the sphere as the reference point, the torque due to the gravitational force will be zero because the line of action of the weight passes through the center of mass.
- If we consider any point along the incline, the gravitational force mg can be resolved into two components:
- mgsinθ (parallel to the incline)
- mgcosθ (perpendicular to the incline)
- The torque due to the normal force N and the component mgcosθ will also be zero at the center of mass since their lines of action pass through this point.
- Since the net torque about the center of mass is zero, the angular momentum of the sphere is conserved as it rolls down the incline.
- However, if we consider points other than the center of mass, the torque due to mgsinθ will not be zero, and thus angular momentum will not be conserved at those points.
The angular momentum of the sphere is conserved at the center of mass of the sphere as it rolls down the smooth inclined plane.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension
71 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A block is released on an smooth inclined plane of inclination θ. After how much time it reaches to the bottom of the plane?

View SolutionA block is released from top of a smooth inclined plane.It reaches the bottom of the plane in 6 sec.The time taken by the body to cover the first half of the inclined plane is:
View Solution
Knowledge Check
A body of mass m and radius r is released from rest along a smooth inclined plane of angle of inclination θ. The angular momentum of the body about the instantanoues point contact after a time t from the instant of release of equal is :
AmgrtcosθBmgrtsinθC(3/2)mgrtsinθDnone of theseA block is released from the top of a smooth inclined plane of inclination θ as shown in figure. Let υ be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
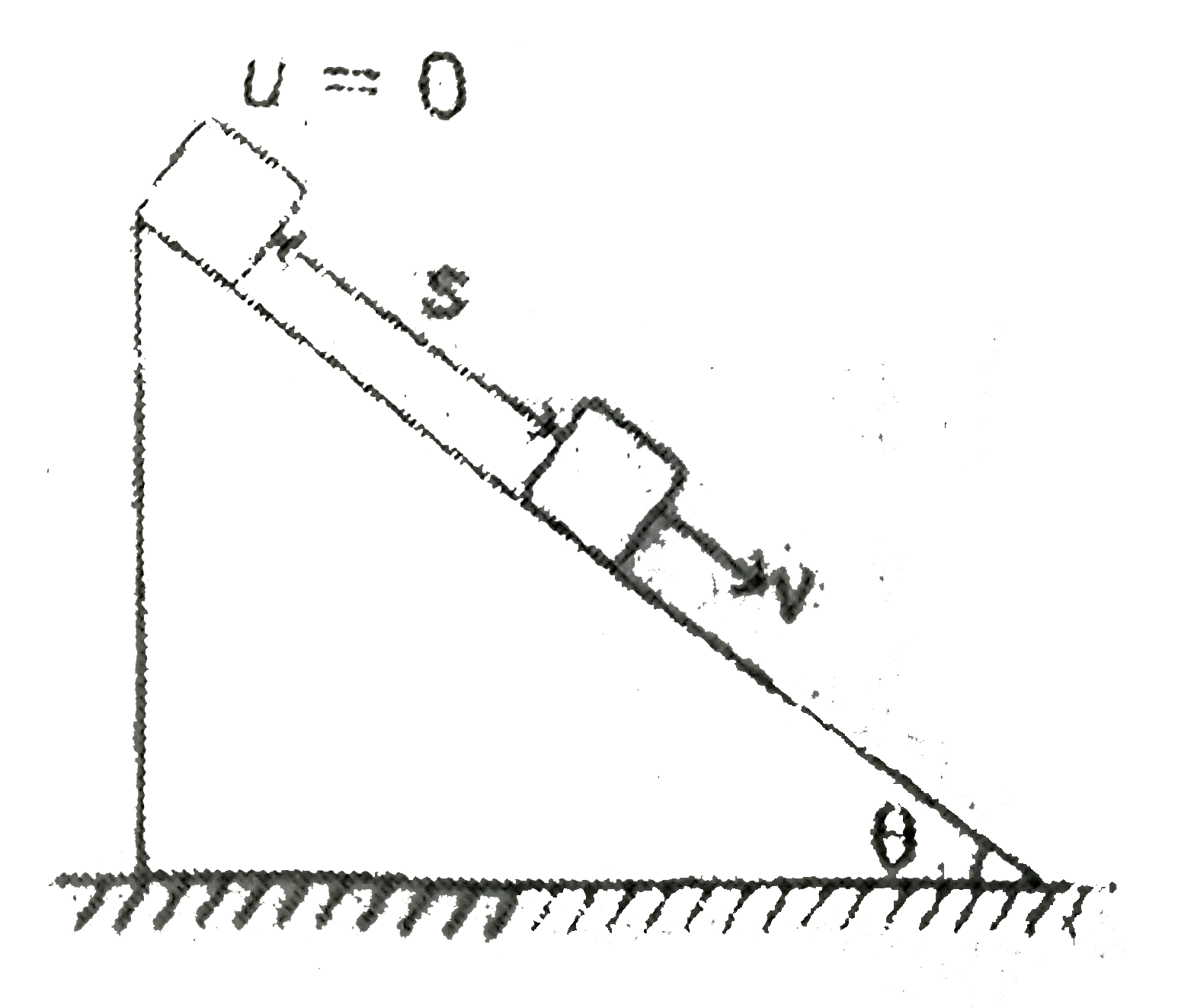 Av2+2gssinθBv2−2gssinθCv−√2gssinθDv+√2gssinθ
Av2+2gssinθBv2−2gssinθCv−√2gssinθDv+√2gssinθA solid sphere rolls down a smooth inclined plane of height h. If it stats from rest then the speed of the sphere when it reaches the bottom is given by
A√ghB√107ghC√47ghD√54gh
A ring of mass M and radius R is at rest at the top of an incline as shown. The ring rolls down the plane without slipping. When the ring reaches bottom, its angular momentum about its centre of mass is:
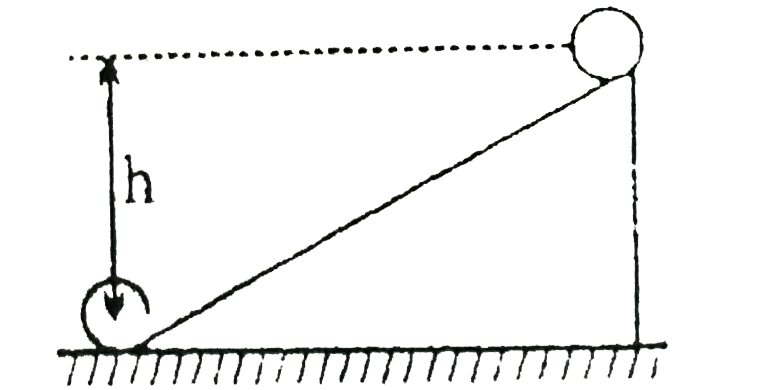
View SolutionA solid sphere is rolling down on inclined plane from rest and a rectangular block of same mass is also slipping down simultaneously from rest on the same plane. Then-
View SolutionA sphere of moment of inertia I rolls down a smooth inclined plane. The ratio of its translation K.E. to the total energy is
View SolutionA solid cylinder is rolling without slipping down an inclined plane. Then its angular momentum is :
View SolutionA solid sphere slides down a smooth inclined plane of inclination θ with acceleration a1. A disc rolls down a rough inclined plane of inclination θ with acceleration a2. Value of a1a2 is
View Solution
