A sphere of mass 40kg is attracted by a second sphere of mass 15kg, when their centres are 20cm apart, with a force of 0.1 miligram weight. Caculate the value of gravitational constant.
To calculate the value of the gravitational constant G, we can use the formula for gravitational force:
F=G⋅m1⋅m2r2
Where:
- F is the gravitational force,
- m1 and m2 are the masses of the two spheres,
- r is the distance between the centers of the two spheres,
- G is the gravitational constant.
Step 1: Identify the given values
- Mass of the first sphere, m1=40kg
- Mass of the second sphere, m2=15kg
- Distance between the centers, r=20cm=0.2m
- Gravitational force, F=0.1mg=0.1×10−6kg⋅g
Here, g (acceleration due to gravity) is approximately 9.8m/s2.
Step 2: Convert the gravitational force to Newtons
The force in Newtons can be calculated as follows:
F=0.1×10−6kg⋅9.8m/s2=0.1×9.8×10−6N=0.98×10−6N
Step 3: Rearrange the formula to solve for G
Rearranging the gravitational force formula gives:
G=F⋅r2m1⋅m2
Step 4: Substitute the values into the equation
Now substitute the known values into the equation:
G=(0.98×10−6)⋅(0.2)240⋅15
Calculating r2:
r2=(0.2)2=0.04m2
Now substituting r2:
G=(0.98×10−6)⋅(0.04)40⋅15
Step 5: Calculate the denominator
Calculating 40⋅15:
40⋅15=600
Step 6: Complete the calculation
Now substitute this back into the equation:
G=(0.98×10−6)⋅(0.04)600
Calculating the numerator:
0.98×10−6⋅0.04=0.0392×10−6
Now divide by 600:
G=0.0392×10−6600=6.53×10−11N m2/kg2
Final Answer
The value of the gravitational constant G is:
G≈6.53×10−11N m2/kg2
---
- F is the gravitational force,
- m1 and m2 are the masses of the two spheres,
- r is the distance between the centers of the two spheres,
- G is the gravitational constant.
- Mass of the first sphere, m1=40kg
- Mass of the second sphere, m2=15kg
- Distance between the centers, r=20cm=0.2m
- Gravitational force, F=0.1mg=0.1×10−6kg⋅g
Here, g (acceleration due to gravity) is approximately 9.8m/s2.
The force in Newtons can be calculated as follows:
Rearranging the gravitational force formula gives:
Now substitute the known values into the equation:
Calculating 40⋅15:
Now substitute this back into the equation:
The value of the gravitational constant G is:
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.113videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 6.215videos
GRAVITATION
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
Two spheres of masses 38 kg and 15 kg each are placed with their centres 20 cm apart. The force of attraction between them is equal to 0.1 milligram wt. Calculate the constant of gravitation.
View SolutionTwo spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
View SolutionTwo spherical balls of mass 10 kg each are placed 100 m apart. Find the gravitational force of attraction between them.
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
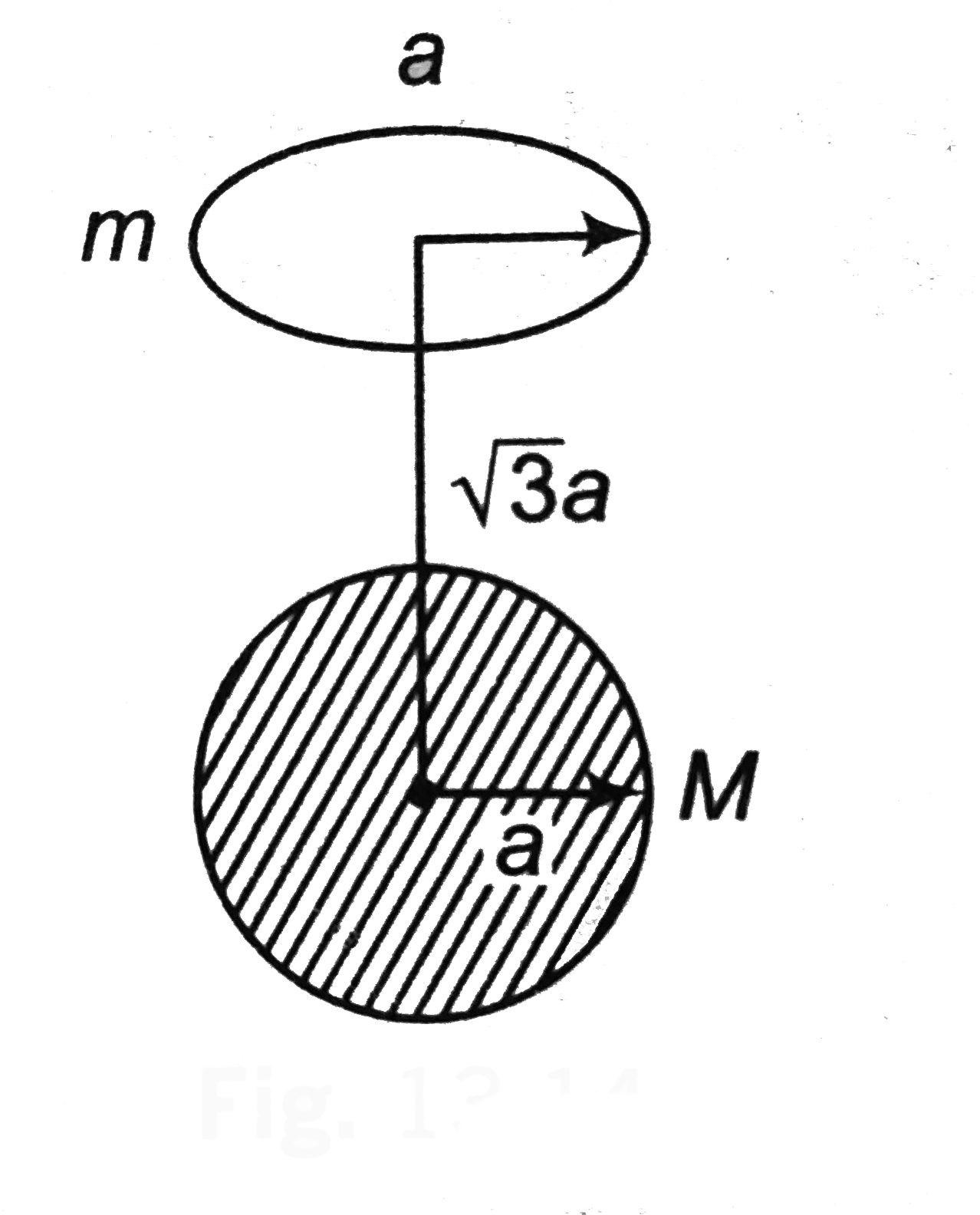 View Solution
View SolutionTwo spheres of masses 16 kg and 4 kg are separated by a distance 30 m on a table. Then, the distance from sphere of mass 16 kg at which the net gravitational force becomes zero is
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
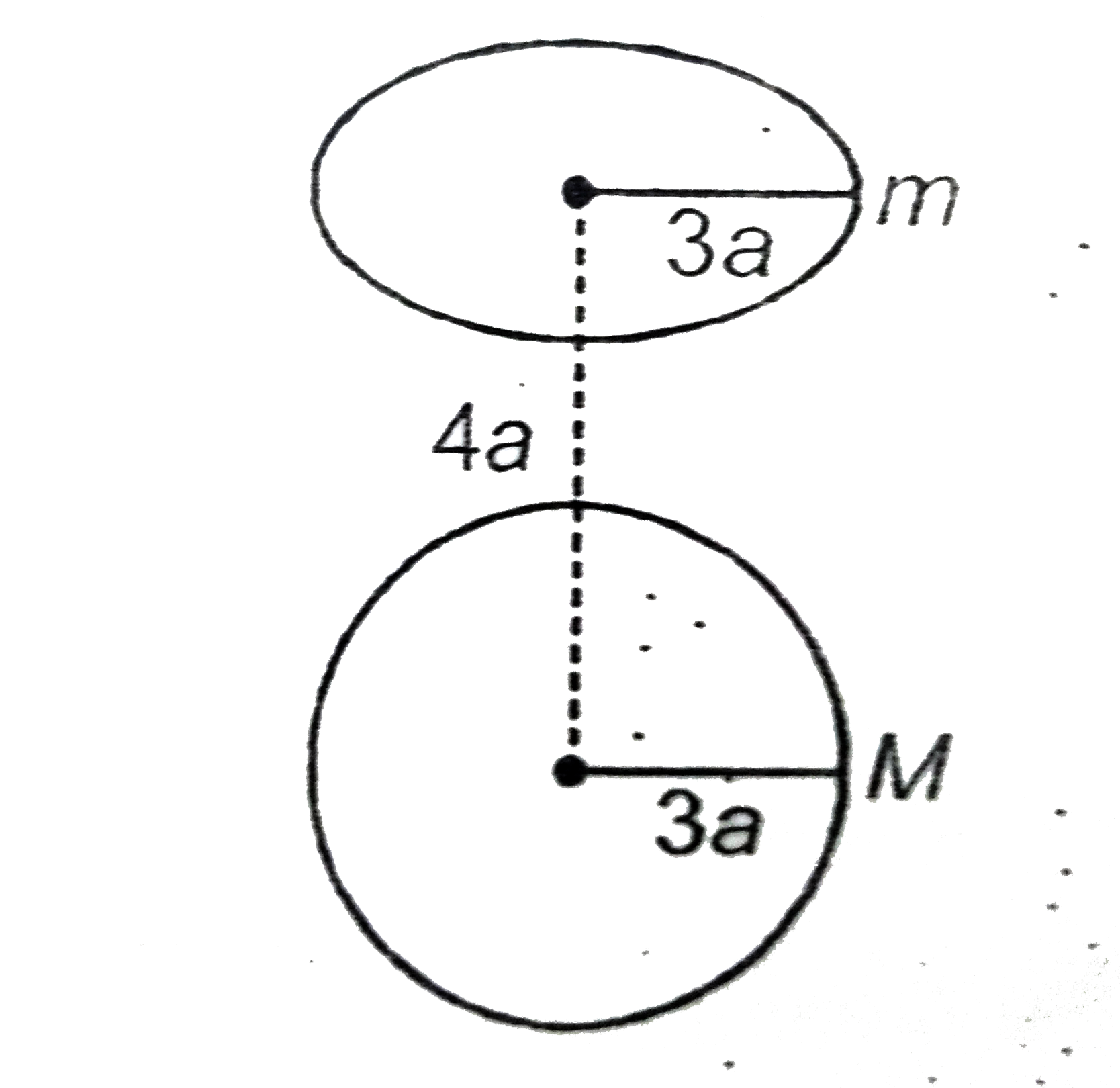 View Solution
View SolutionA body of mass 1 kg is attracted by the Earth with a force which is equal to _______________
View Solution

