A sphere of radius 0.1 m and mass 8 pi kg is attached to the lower end

A sphere of radius $0.1 m$ and mass $8 π$ $k g$ is attached to the lower end of a steel wire of length $5.0 m$ and diameter $10^{- 3} m$ . The wire is suspended from $5.22 m$ high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is $(1.994 \times 10^{11} N / m^{2})$ .
A $7.7 m s^{- 1}$
B $4.4 m s^{- 1}$
C $2.2 m s^{- 1}$
D $8.8 m s^{- 1}$
A sphere of mass $m$ attached with the free end of a steel wire of length $l$ swings in the veritical plane form the horizontal positon.

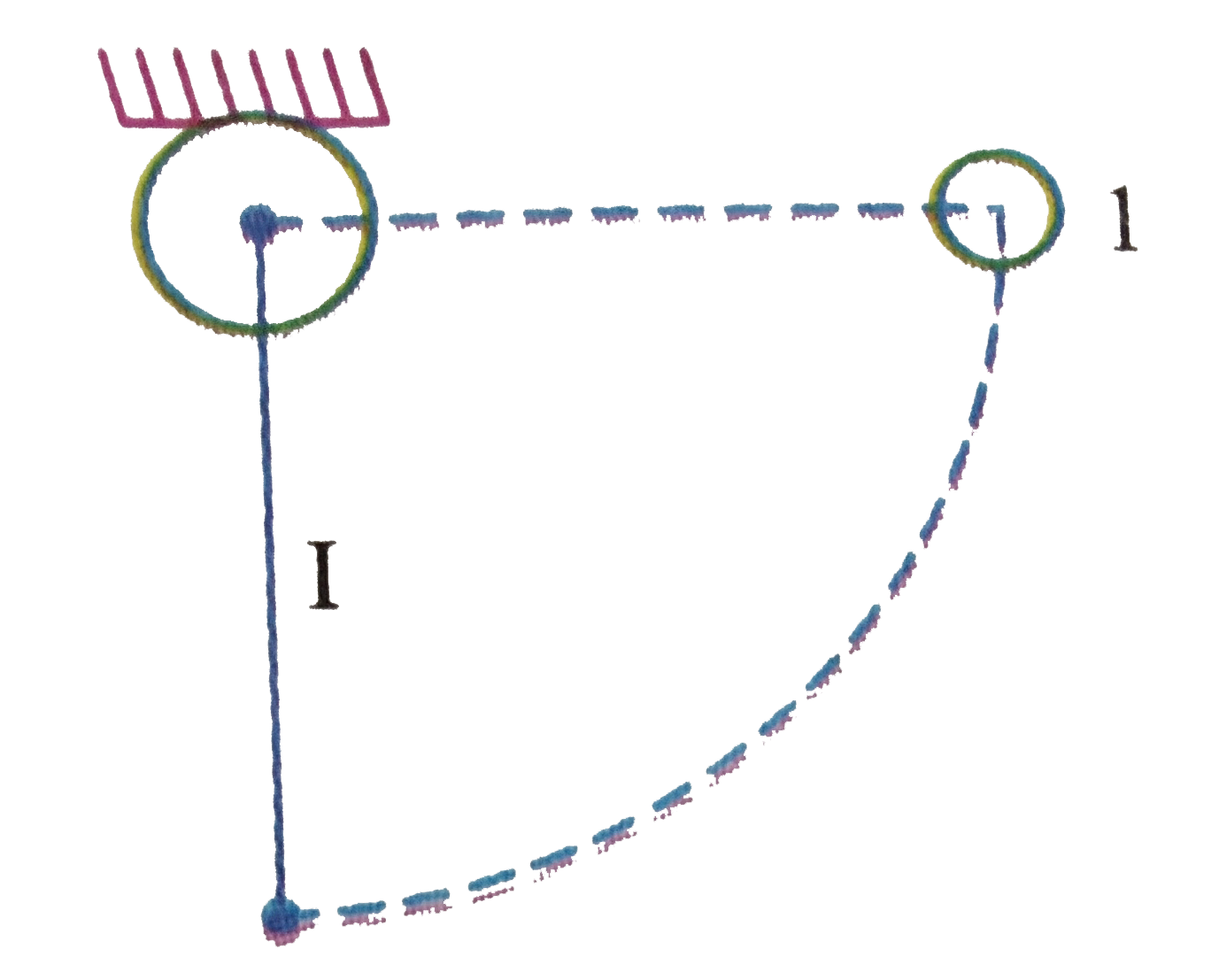
Elongation of the wire in the vericle positon is
A $\frac{m g l}{Y (π r^{2})}$
B $\frac{2 m g l}{Y (π r^{2})}$
C $\frac{m g l}{3 Y (π r^{2})}$
D $\frac{3 m g l}{Y (π r^{2})}$
A uniform steel wire of length 3.14 m and diameter $2 \times 10^{- 3}$ m is fixed at its upper end. When a mass of 10 kg is attached to its lower end, the extension of the wire is $1 \times 10^{- 3}$ m. The Young's modulus of elasticity is,
A $9.8 \times 10^{8} N / m^{2}$
B $9.8 \times 10^{9} N / m^{2}$
C $9.8 \times 10^{10} N / m^{2}$
D $9.8 \times 10^{11} N / m^{2}$

The correct Answer is:C