A sphere of radius 10cm and mass 25kg is attached to the lower end of a steel wire which is suspended from the ceiling of a room. The point of support is 521cm above the floor. When the sphere is set swimming as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position.
Young's modulus of steel=20×1010N/m2
Unstretched length of the wire =500cm
Radius of the steel wire =0.05cm
A wire can be considered as a spring of suitable force constant. For a wire
Y=FA△l/l=FLA△l⇒F=YAll△l
Now F=k.△l
Therefore k (force cosnant =F△l=YAl
⇒k=20×1010×π(0.05×10−2)25=π×10N/m2
Now we may treat the problem as if the mass were suspended by a spring of force constant k=104πN/m2. Considering the dynamics of circular motion at the lowest point
T−mg=mv2r
Obviously, at the lowest point the wire elongates by 1cm
∴T=k△l=π×104×0.01=π×102N
∴π×102−25×9.8=25×v25.21
v2=(100π−245)×5.2125=14.42
⇒v=3.8ms−1
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.2
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2).
View SolutionA sphere of radius 0.1m and mass 8πkg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View Solution
Knowledge Check
A sphere of radius 0.1m and mass 8π kg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3m. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
A7.7ms−1B4.4ms−1C2.2ms−1D8.8ms−1A steel wire 2m long is suspended from the ceiling. When a mass is hung from its lower end, the increase in length recorded is 1cm. Determine the strain in the wire.
A0.002B0.005C0.008D0.002The free and of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point the box is released to fall freely. As sen from the box during this period the bob will
Acontinue its oscillation as beforeBstopCwill go in a circular pathDmove on a straight line
A light elastic string is suspended vertically from a point and carries a heavy mass at its lower end , which stetches innature and its time period is equal to that of a simple pendulum of length l.
View SolutionA wagon of mass M can move without friction along horizontal rails. A simple pendulum consisting of a sphere of mass m is suspended from the ceiling of the wagon by a string of length l. At the initial moment the wagon and the pendulum are at rest and the string is deflected through an angle α from the vertical. Find the velocity of the wagon when the pendulum passes through its mean position.
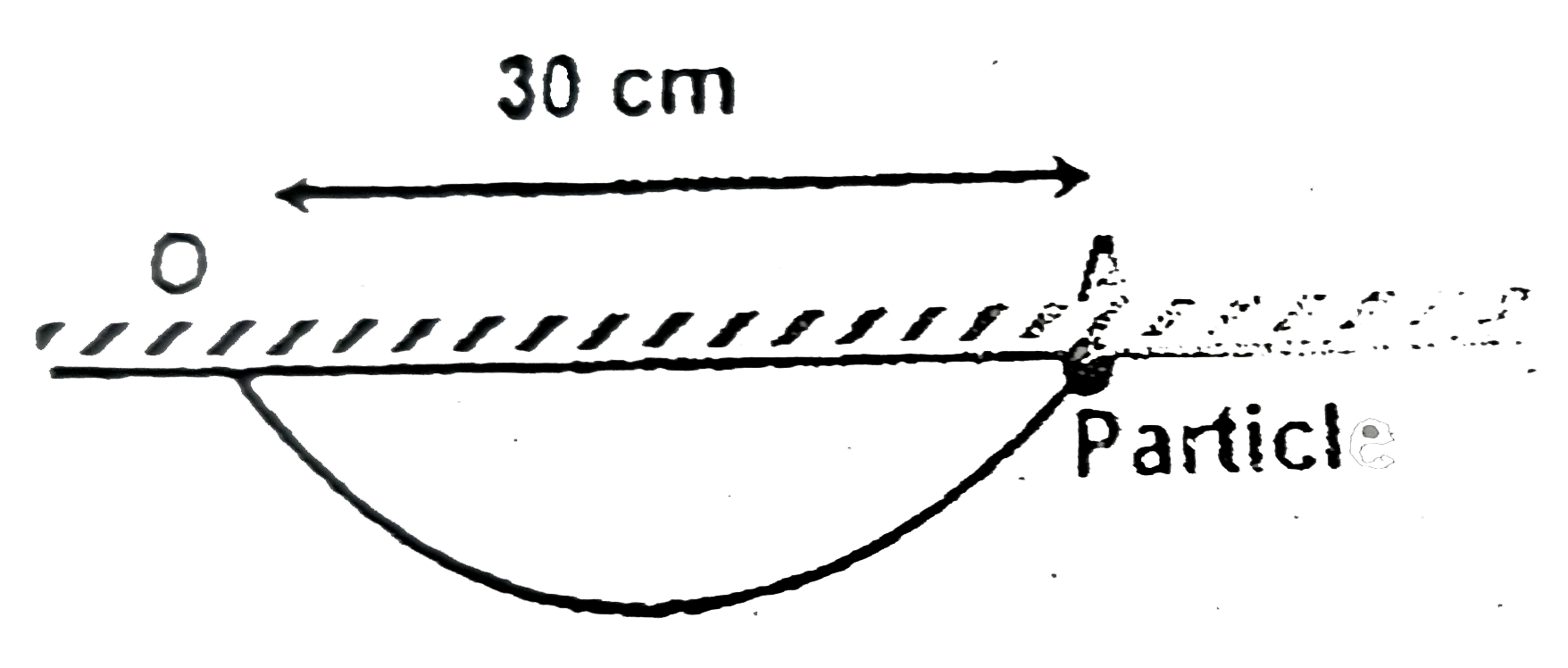
View SolutionA small ball of mass 100g is attached to a light and inextensible string of length 50cm. The string is tied to a support O and the mass m released from point A which is a' a horizontal distance of 30cm from the support. Calculate the speed of the ball is its lowest point of the trajectory.
View SolutionA body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neigther stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation ?
(b) Find the frequency of oscillation?
View SolutionA body of mass m is attached ot one end of a massless spring which is suspended vertically form a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. The lowest position attained by the mass during oscillation is 4 cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation?
(b) Find the frequency of oscillation?
View Solution
