A spinning cylinder of mass m and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
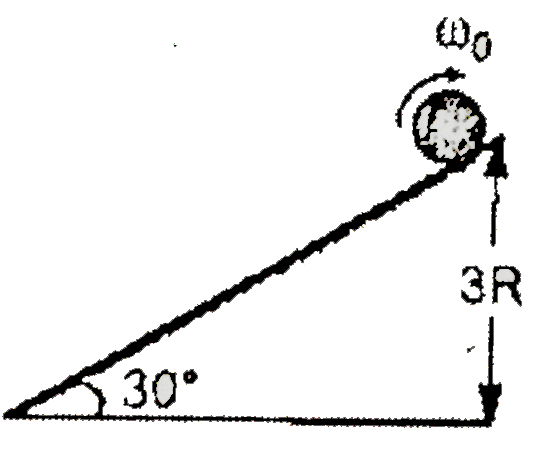
Step by step video & image solution for A spinning cylinder of mass m and radius R is lowered on a rough inclined plane of angle 30^(@) with the horizontal and mu=1sqrt(3). The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE83videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MCQ_TYPE41videos
RIGID BODY MOTION
- BOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching3videos
IMPULSE AND MOMENTUM
- BOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem4videos
UNIT AND DIMENSIONS
Similar Questions
A spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
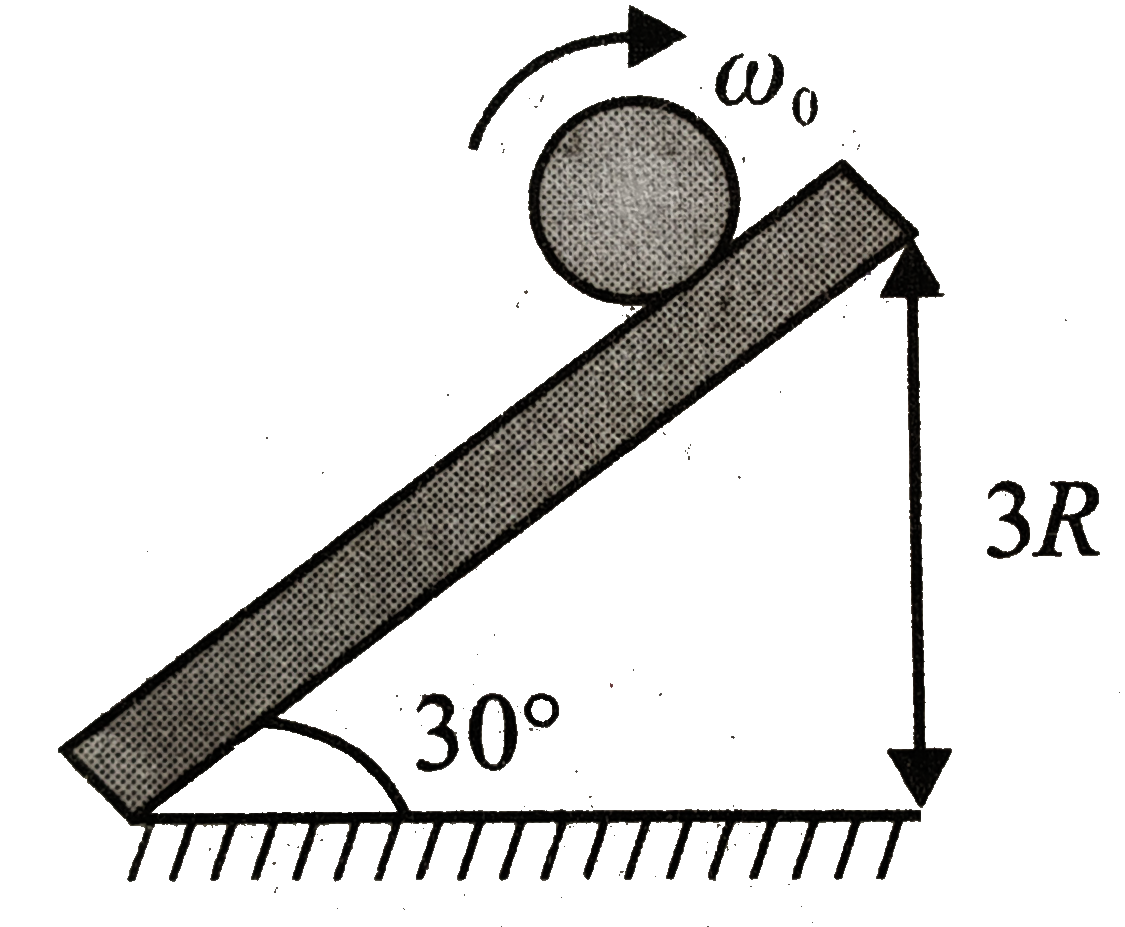 View Solution
View SolutionA solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A√34ghB√43ghC√4ghD√2gh - Question 2 - Select One
A cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
A12Mv2B12Iω2C34Mv2D34Iω2 - Question 3 - Select One
A cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
A12Mv2B12Iω2C34Mv2D34Iω2
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View Solution
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k isView Solution

