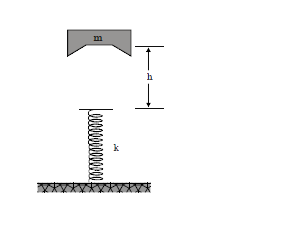
A spring gets compressed when a body of mass 5 g is dropped on it from a height of 2 m . Calculate the maximum distance s through whichthe spring is compressed. The force constant of spring is 100Nm−1 .
To solve the problem step by step, we will use the principles of energy conservation and the work-energy theorem.
Step 1: Identify the given data
- Mass of the body, m=5g=0.005kg
- Height from which the body is dropped, h=2m
- Spring constant, k=100N/m
Step 2: Calculate the gravitational potential energy (PE) of the body at height h
The gravitational potential energy can be calculated using the formula:
PE=mgh
Substituting the values:
PE=0.005kg×9.81m/s2×2m
PE=0.005×9.81×2=0.0981J
Step 3: Set up the equation for the maximum compression of the spring
At maximum compression s, all the potential energy will be converted into the elastic potential energy (EPE) of the spring:
PE=EPE
The elastic potential energy stored in the spring is given by:
EPE=12ks2
Equating the two energies:
0.0981=12×100×s2
Step 4: Solve for s2
Rearranging the equation:
0.0981=50s2
s2=0.098150
s2=0.001962
Step 5: Calculate s
Taking the square root to find s:
s=√0.001962≈0.0443m
Final Answer
The maximum distance through which the spring is compressed is approximately:
s≈0.0443m or 4.43cm
---
- Mass of the body, m=5g=0.005kg
- Height from which the body is dropped, h=2m
- Spring constant, k=100N/m
The gravitational potential energy can be calculated using the formula:
PE=mgh
Substituting the values:
PE=0.005kg×9.81m/s2×2m
PE=0.005×9.81×2=0.0981J
At maximum compression s, all the potential energy will be converted into the elastic potential energy (EPE) of the spring:
PE=EPE
The elastic potential energy stored in the spring is given by:
EPE=12ks2
Equating the two energies:
0.0981=12×100×s2
Rearranging the equation:
0.0981=50s2
s2=0.098150
s2=0.001962
Taking the square root to find s:
s=√0.001962≈0.0443m
The maximum distance through which the spring is compressed is approximately:
s≈0.0443m or 4.43cm
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (A. Multiple Choice Questions)
29 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (B. Multiple Choice Questions)
46 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Revision Exercise (Long Answer Questions)
9 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A block of massm, initally at rest is dropped from a height h onto a spring whose force constant is K. Find the maximum distance x through which the spring will be compressed.
View SolutionA block of mass m = 2.0 kg is dropped from height h = 40 cm onto a spring of spring constant k=1960N/s. Find the maximum distance through which the spring is compressed. Take g=9.8m/s2
View Solution
Knowledge Check
A block of mass 2kg is propped from a height of 40cm on a spring where force constant is 1960Nm−1 The maximum distance thought which the spring compressed by
A5cmB15cmC26cmD10cmA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2
A spring is compressed by a toy cart of mass 150g. On releasing the cart, it moves with a speed of 0.2m/s. Calculate the elastic potential energy of the spring.
View SolutionA block of mass 2 kg initially at rest is dropped from a height of 1m into a vertical spring having force constant 490Nm−1. Calculate the maximum distance through which the spring will be compressed.
View SolutionOn compressing a spring by 0.5 m, a restoring force of 20 N is developed. When a body of mass 5 kg is placed on the spring, then calculate the (a) force constant of the spring.
(b) the distance through which the spring is depressed under the weight of the body.
(c ) the period of oscillation of the spring if the the body is pushed down and then released.
View SolutionA block of mass 5.7kg slides on a horizontal frictionless table with a constant speed of 1.2ms−1. It is brougth momentarily to rest by compressing a spring in its path. By what maximum distance is the spring compressed ? The spring constant k=1500Nm−1.
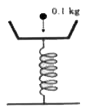
View SolutionA massless platform is kept on a light elastic spring, as shown in the figure. When particle of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the particle strikes the pan, and the spring is compressed by 0.01 m. From what height should the particle be dropped to cause a compression of 0.04 m?
View Solution
