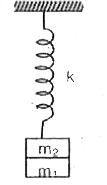
A spring is loaded with two blocks m1 and m2 where m1 is rigidly fixed with the spring and m2 is just kept on the block m1. The maximum energy of oscillation is possible for the system having the block m2 in constant with m1 is
m21g2k
m1g22k
m22g22k
(m1+m2)2g22k
The correct Answer is:D
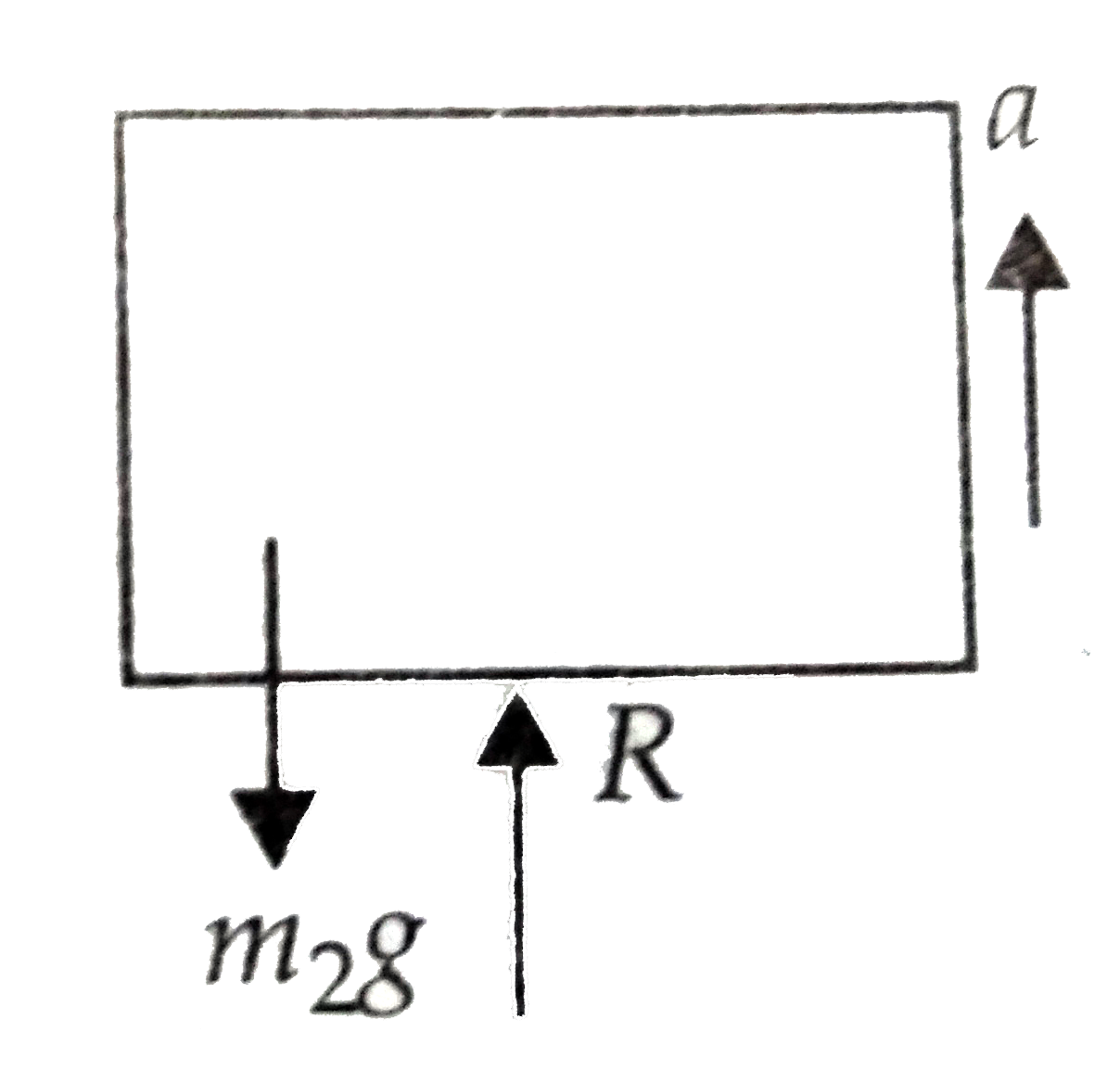
let x be the required amplitude of oscillation for this amplitude of oscillation the normal contact force between the blocks can be given by
R−m2g=m2a
where, acceleration
a=−ω2x
∴R−m2g=−m2ω2x
For maximum amplitude of
oscillation without loosing contact
of block m2 with block m1, R=0
we get, x=g/ω2
Where ω is the angular frequency of oscillation of (m1+m2) and spring. therefore
ω=√k(m1+m2) or ω2=k(m1+m2)
⇒x=(m1+m2)gk
Hence, the maximum energy of oscillation
umax=12kx2=(m1+m2)2g22k
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar
10 Videos
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
1 Videos
- OSCILLATIONS BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Forced Oscillation And Resonance
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason
15 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTIPSCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Block of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
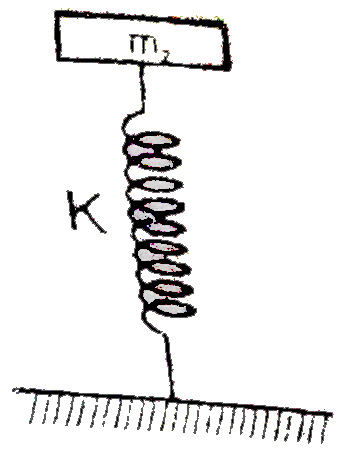
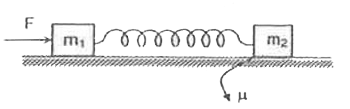
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
View Solution
Knowledge Check
A spring is loaded with two blocks m1andm2 where m1 is rigidly fixed with the spring and m2 is just kept on the block m1 as shown in the figure. The maximum energy of oscillation that is possible for the system having the block m2 in constact with m1 is
 Am21g22kBm22g22kC(m1+m2)2g22kDnone of these
Am21g22kBm22g22kC(m1+m2)2g22kDnone of theseTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2
Am2gm1+m2Bm1gm1+m2C4m2g−m1gm1+m2Dm2gm1+4m2Two blocks of mass m1 and m2, resting on a frictionless table, are connected by a stretched spring and then released -
Aratio of speed of blocks is m2/m1Bratio of kinetic energy of blocks is m2/m1Ccentre of mass will move towards heavier blockDmechanical energy will remain conserve in this process
Two blocks m1 and m2 are allowed to move without friction. Block m1 is on block m2 and m2 slides on smooth fixed incline as shown. The angle of inclination of inclined plane is θ
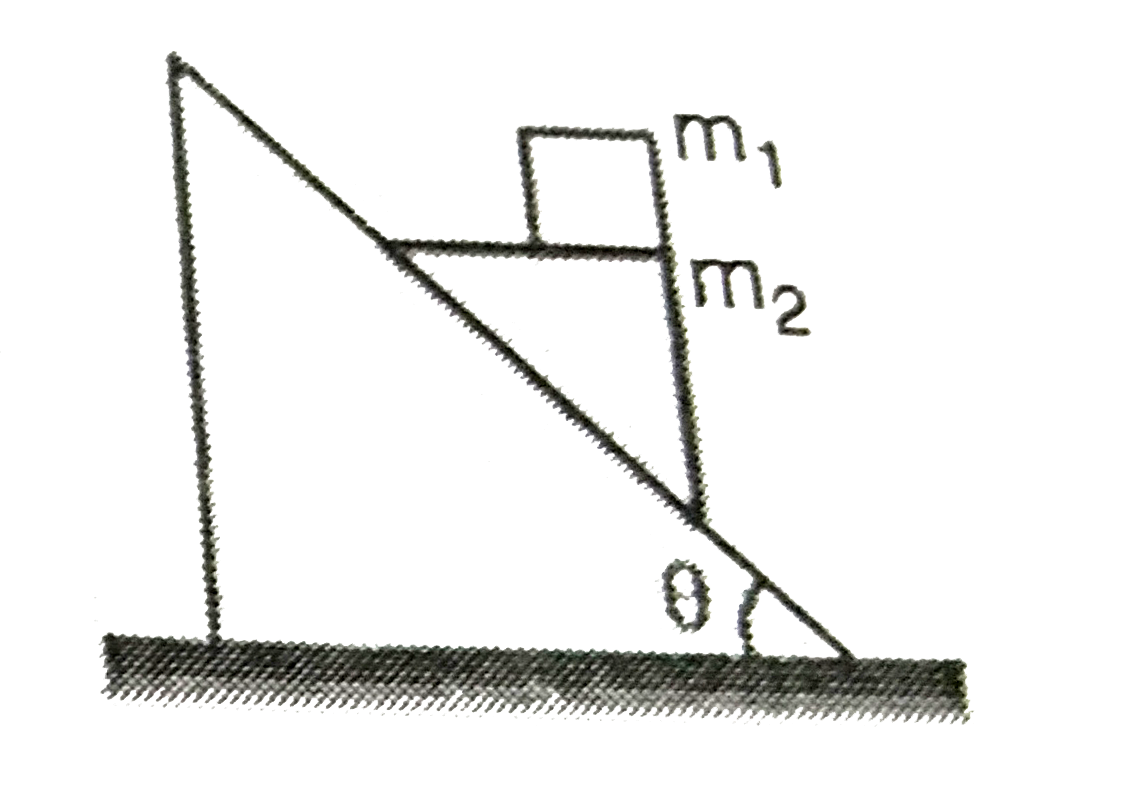
The acceleration of m1 with respect to ground is:
View SolutionTwo blocks m1 and m2 are allowed to move without friction Block m1 is on block m2 and m2 slides on smooth fixed incline as shown The angle of inclination of inclined plane is θ
 .
.
Normal reaction on m1 is .
View SolutionTwo blocks m1 and m2 are allowed to move without friction Block m1 is on block m2 and m2 slides on smooth fixed incline as shown The angle of inclination of inclined plane is θ
 .
.
The acceleration of m2 with respect to ground is .
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View SolutionTwo blocks of masses m1 and m2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m2) drops off. The other block (m1) will

View Solution
