A square loop of side 20 cm is placed on a plane and magnetic field intensity of 0.1 T is applied at an angle 30∘ with the plane of the loop. Magnetic field is changed to zero uniformly within 0.8 second. Calculate the induced emf and current in the loop.
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the Area of the Square Loop
The area A of a square loop with side length s is given by:
A=s2
Given that the side length s=20cm=0.2m:
A=(0.2m)2=0.04m2
Step 2: Determine the Angle Between the Magnetic Field and the Area Vector
The magnetic field B is applied at an angle of 30∘ with the plane of the loop. Therefore, the angle θ between the magnetic field and the area vector A (which is perpendicular to the plane) is:
θ=90∘−30∘=60∘
Step 3: Calculate the Initial Magnetic Flux
The magnetic flux Φ through the loop is given by:
Φ=B⋅A⋅cos(θ)
Substituting the values:
- B=0.1T
- A=0.04m2
- θ=60∘ (where cos(60∘)=12):
Φ=0.1T⋅0.04m2⋅12=0.002Wb
Step 4: Calculate the Change in Magnetic Flux
Since the magnetic field changes from 0.1T to 0T, the change in magnetic flux ΔΦ is:
ΔΦ=Φfinal−Φinitial=0−0.002Wb=−0.002Wb
Step 5: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Since the change in flux occurs uniformly over a time interval Δt=0.8s:
E=−−0.002Wb0.8s=0.0020.8=0.0025V=2.5mV
Step 6: Calculate the Current in the Loop
To find the current I, we use Ohm's law:
I=ER
However, the resistance R of the loop is not provided in the question. Therefore, we cannot calculate the current without this information.
Summary of Results
- Induced EMF E=2.5mV
- Current I cannot be calculated without the resistance R.
The area A of a square loop with side length s is given by:
A=s2
Given that the side length s=20cm=0.2m:
A=(0.2m)2=0.04m2
The magnetic field B is applied at an angle of 30∘ with the plane of the loop. Therefore, the angle θ between the magnetic field and the area vector A (which is perpendicular to the plane) is:
θ=90∘−30∘=60∘
The magnetic flux Φ through the loop is given by:
Φ=B⋅A⋅cos(θ)
Substituting the values:
- B=0.1T
- A=0.04m2
- θ=60∘ (where cos(60∘)=12):
Φ=0.1T⋅0.04m2⋅12=0.002Wb
Since the magnetic field changes from 0.1T to 0T, the change in magnetic flux ΔΦ is:
ΔΦ=Φfinal−Φinitial=0−0.002Wb=−0.002Wb
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Since the change in flux occurs uniformly over a time interval Δt=0.8s:
E=−−0.002Wb0.8s=0.0020.8=0.0025V=2.5mV
To find the current I, we use Ohm's law:
I=ER
However, the resistance R of the loop is not provided in the question. Therefore, we cannot calculate the current without this information.
- Induced EMF E=2.5mV
- Current I cannot be calculated without the resistance R.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE PROBLEMS25videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS22videos
ELECTROMAGNETIC INDUCTION
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
Similar Questions
A square loop of side 20 cm is placed on a plane and magnetic field intensity of 0.1 T is applied at an angle 30 with the plane of the loop. Magnetic field is changed to zero uniformly within 0.8 second. Calculate the emf induced in the loop.
View SolutionA square loop of side 20 cm and resistance 0.30 Ω is placed in a magnetic field of 0.4 T. The magnetic field is at an angle of 45∘ to the plane of loop. If the magnetic field is reduced to zero in 0.5 s, then find the induced emf and induced current in the loop in this time interval.
View Solution
Knowledge Check
- Question 1 - Select One
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0Iπa - Question 2 - Select One
A square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πa - Question 3 - Select One
A square loop of side 5 cm enters a magnetic field with 1cms−1. The front edge enters the magnetic emf?
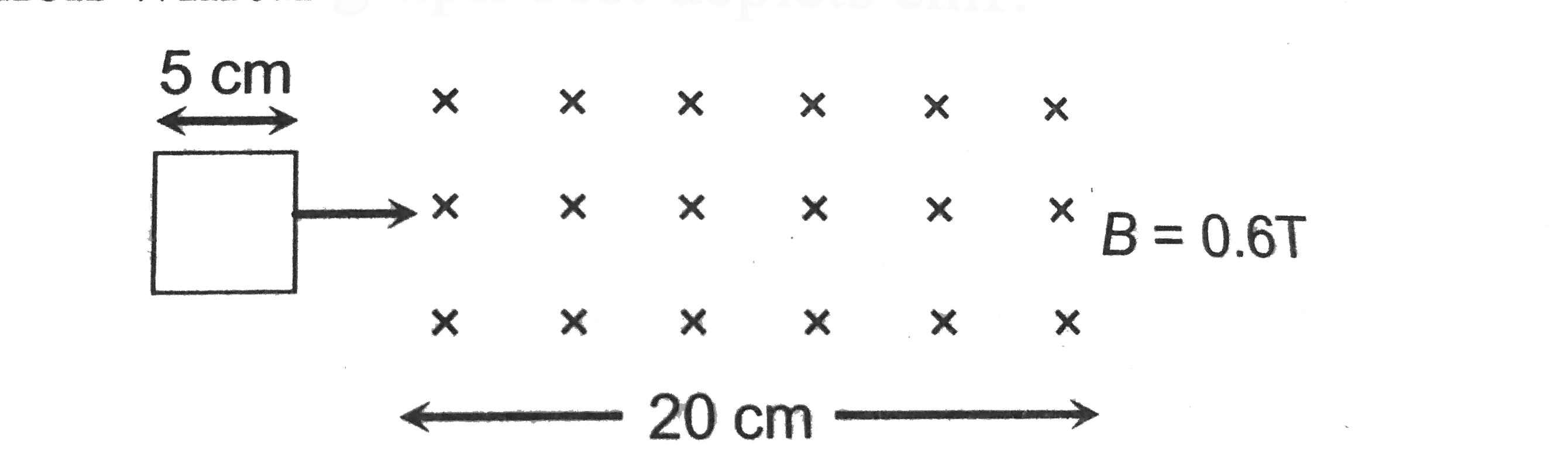 A
A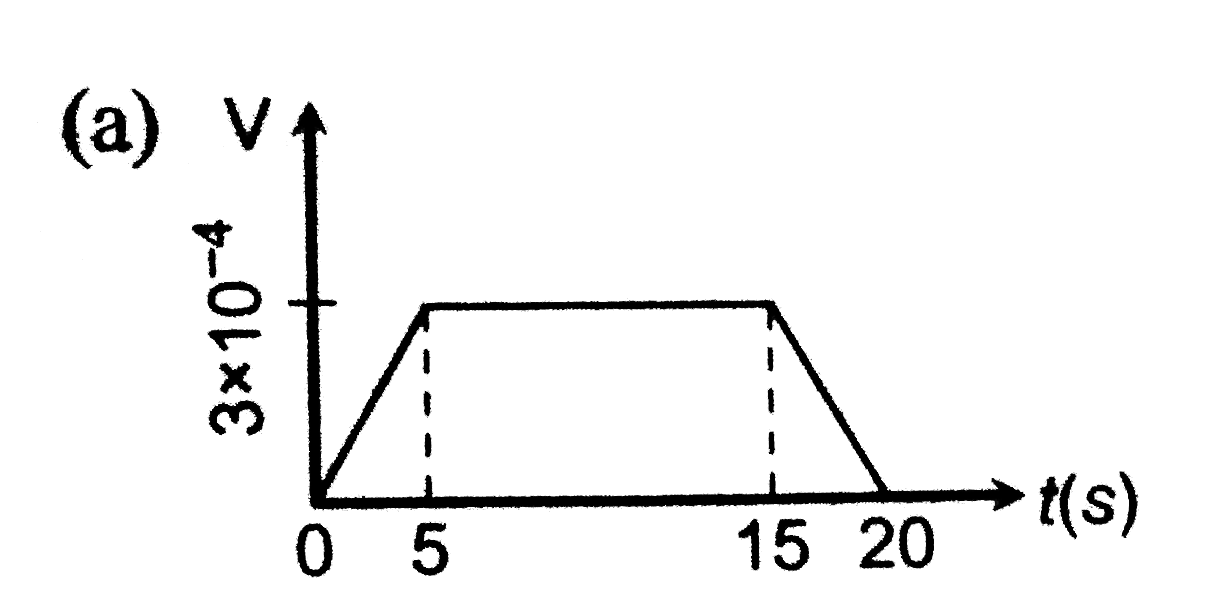 B
B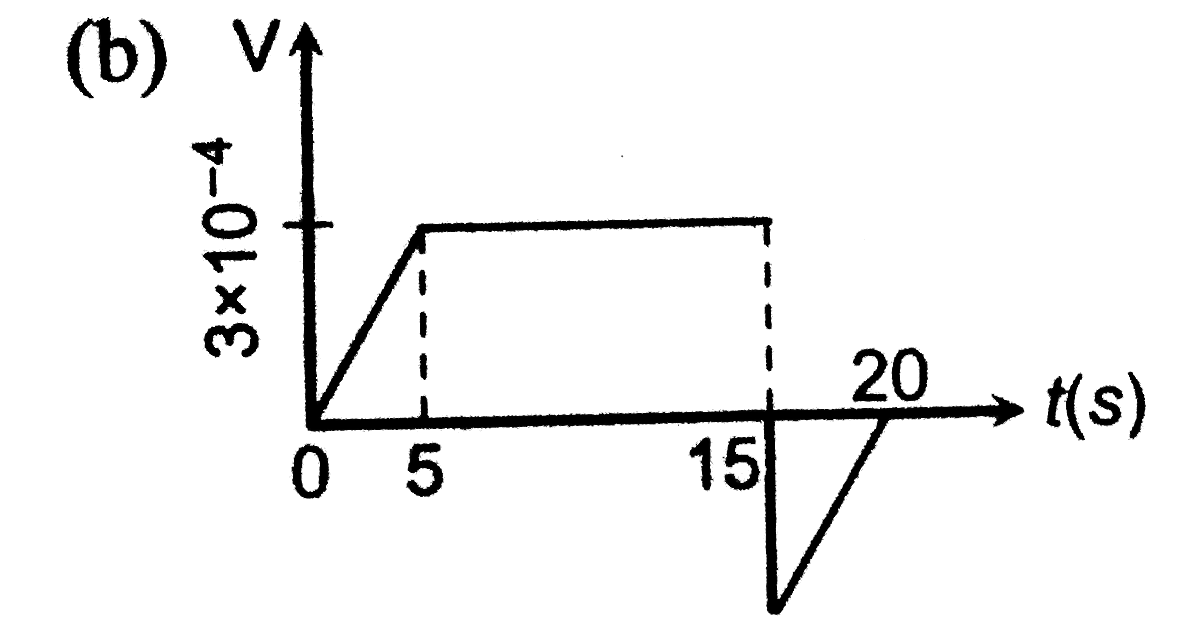 C
C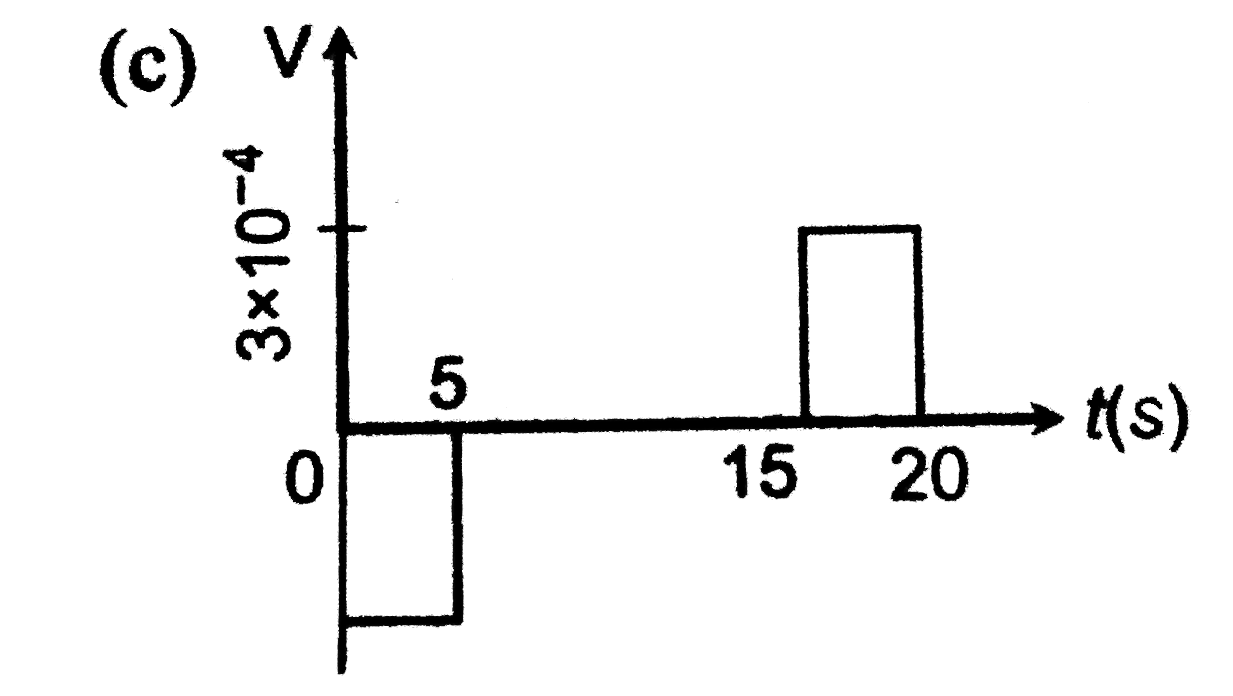 D
D
A circular loop is placed in a uniform magnetic field of 0.30 T. The plane of the loop is at an angle of 90∘ to the field. The radius of the loop is decreasing at the rate of 2mm/s. Calculate the induced emf in the coil when the radius of the loop becomes 1 cm.
View SolutionA circular loop of radius 10 cm is placed in a region of magnetic field of 0.5 T with its plane parallel to the magnetic field. Calculate the magnetic flux through the coil.
View SolutionA square loop of side 10cm and resistance 0.5Ω is placed vertically in the east-west plane. A uniform magnetic field of 0.10T is set up across the plane in the north-east direction. The magnetic field is decreased to zero in 0.70s at a steady rate. The magnetude of current in this time-interval is.
View SolutionA circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
View SolutionA square loop of side 22cm is converted into circular loop in 0.4s. A uniform magnetic field of 0.2Tdirected normal to the loop, then the induced in the loop is
View Solution

