A standing wave is formed by the superposition of two waves travelling in the opposite directions. The transverse displacement is given by
y(x,t)=0.5sin(5π4x)cos(200πt)
What is the speed of the travelling wave moving in the postive X direction ?
160 m/s
90 m/s
180 m/s
120 m/s
The correct Answer is:A
To find the speed of the traveling wave moving in the positive x direction from the given standing wave equation, we can follow these steps:
1. Identify the standing wave equation: The given equation is
y(x,t)=0.5sin(5π4x)cos(200πt)
This is in the form of a standing wave, which can be expressed as
y(x,t)=2asin(kx)cos(ωt)
where a is the amplitude, k is the wave number, and ω is the angular frequency.
2. Extract the wave number (k) and angular frequency (ω): From the equation, we can identify:
- k=5π4
- ω=200π
3. Use the relationship between speed (v), wave number (k), and angular frequency (ω): The relationship is given by:
ω=v⋅k
Rearranging this gives us:
v=ωk
4. Substitute the values of ω and k into the equation:
v=200π5π4
5. Simplify the expression:
- First, simplify the fraction:
v=200π⋅45π
- The π terms cancel out:
v=200⋅45
- Now calculate:
v=200⋅0.8=160 m/s
6. Conclusion: The speed of the traveling wave moving in the positive x direction is
v=160 m/s
y(x,t)=0.5sin(5π4x)cos(200πt)
This is in the form of a standing wave, which can be expressed as
y(x,t)=2asin(kx)cos(ωt)
where a is the amplitude, k is the wave number, and ω is the angular frequency.
- k=5π4
- ω=200π
ω=v⋅k
Rearranging this gives us:
v=ωk
v=200π5π4
- First, simplify the fraction:
v=200π⋅45π
- The π terms cancel out:
v=200⋅45
- Now calculate:
v=200⋅0.8=160 m/s
v=160 m/s
Topper's Solved these Questions
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - ASSERTION REASON TYPE QUESTIONS
11 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - MATCHING TYPE QUESTIONS
3 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - REVISION EXERCISES
107 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string
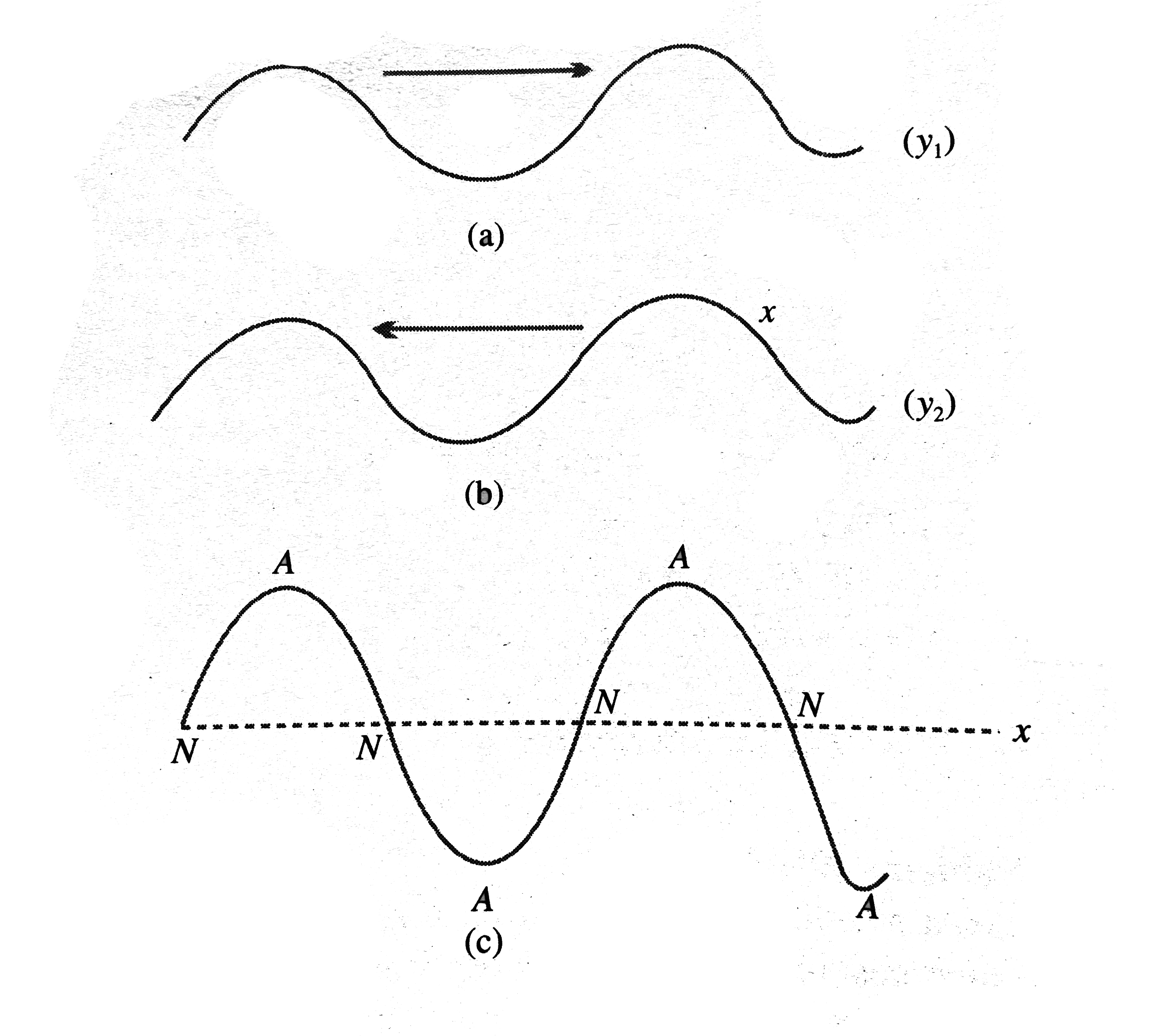
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Maximum value of the y - positions coordinate in the simple harmonic motion of an element of the string that is located at an antinode will be
View Solution
Knowledge Check
A standing wave is formed by the superposition of two waves travelling in opposite directions. The transverse displacement is given by y(x,t)=0.5sin(5π4x)cos(200πt) What is the speed of the travelling wave moving in the position x direction?
A160m/sB90m/sC180m/sD120m/sConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
If one end of the string is at x=0 , positions of the nodes can be described asAx=nπ/5cm,wheren=0,1,2,…Bx=n2π/5cm,wheren=0,1,2,…Cx=nπ/5cm,wheren=0,1,3,5,…Dx=nπ/10cm,wheren=0,1,3,5,…Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will beA3.3cmB6.7cmC4.9cmD2.6cm
Two waves travelling in opposite directions produce a standing wave . The individual wave functions are given by y1=4sin(3x−2t) and y2=4sin(3x+2t)cm , where x and y are in cm
View SolutionThe displacement y of a wave travelling in the x-direction is given by
y=10−4sin(600t−2x+π3)m
Where x is expressed in metre and t in seconds. The speed of the wave motion in m/s is
View SolutionThe equation of a progressive wave is given by, y=5sinπ(t0.02−x20)m, then the frequency of the wave is
View SolutionA wave travels in a medium according to the equation of displacement given by
y(x,t)=0.03sinπ(2t−0.01x)
where y and x are in metres and t in seconds. The wavelength of the wave is
View SolutionThe equation of a progressive wave travelling on a strected string is y=10sin2π(t0.02−x100) where x and y are in cm and t is in sec. What is the speed of the wave?
View Solution
