A steel bar ABCD40cm long is made up of three parts AB,BC and CD, as shown in figure. The rod is subjected to a pull of 25kN. Determine the stress in the thre parts and the total extension of the rod. Young's modulys for steel=2×1011nm−2.

Method1: The axial force 25kN is transmitted to each of the three bars.
Stress in part AB is
25000Nπ4(50)2mm2=40π=12.73N/mm2
Stress in part BC=25000π4(25)2=50.93N/mm2
Stress in part CD=12.73N/mm2
Therefore, total extension of the rod = extension in the parts AB+BC+CA
=(12.73Nmm22×105N/mm2×10mm)×2+50.93Nmm22×105N/mm2×200mm
=127322×105mm=0.0637mm
Method 2: The steel bar ABCD can be replaced with series combination of three springs.
Equivalent spring contact can be written as 1keq=1k1+1k2+1k1
Here k1=YA1l1 and k2=YA2l2

which gives keq=Y(A1A2)(2A2l1+A1l2)
Extension of composite rod x=Fkeq
This gives x=F(2A2l2+A1l2)YA1A2=15πmm=0.0637mm
In series combination of springs the force in each spring should be equal. hence, each rod will experiecne same force F.
Hence stress is rods AB and CD is
σAB=σCD=FA1=25×103(π4×502)=40πN/mm2
Stress in rod BC is
25×103(π4×252)=160πN/mm2
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Solved Examples
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Exercise 5.1
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Video
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
One end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceilign and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View Solution
Knowledge Check
When a steel wire is subject to a stress of 3.8×105N/m2, its length is increased by 2 part in a million. The Young's modulus jof steel is
A6.4×1011N/m2B1012N/m2C1.6×1010N/m2D1.9×1011N/m2When a steel wire is subject to a stress of 3.8×105N/m2, its length is increased by 2 part in a million. The Young's modulus jof steel is
A19×1011N/m2B9.5×1011N/m2C3.8×1011N/m2D1.9×1011N/m2Two wires of equal cross-section but one made of steel and the other of copper are joined end to end. When the cobination is kept under tension, the elongations in the two wires are found to be equal elongations in the two wire are found to be equal. What is the ratio of the lengths of the two wires?
(Given, Young's modulus of steel =2×1011Nm−2 and young's modulus of copper =1.1×1011Nm−2)A2:11B11:2C20:11D11:20
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
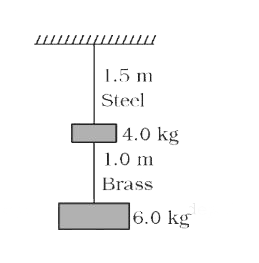
View SolutionHow much will a 30 m steel tape 1 cm wide and 0.05 cm thick stretch under a pull of force of 300 N , if Young's modulus of steel is 2×1011Nm−2?
View SolutionA steel rod of cross-sectional area 1m2 is acted upon by forces as shown in the Fig. Determine the total elongation of the bar. Take Y=2.0×1011N/m2
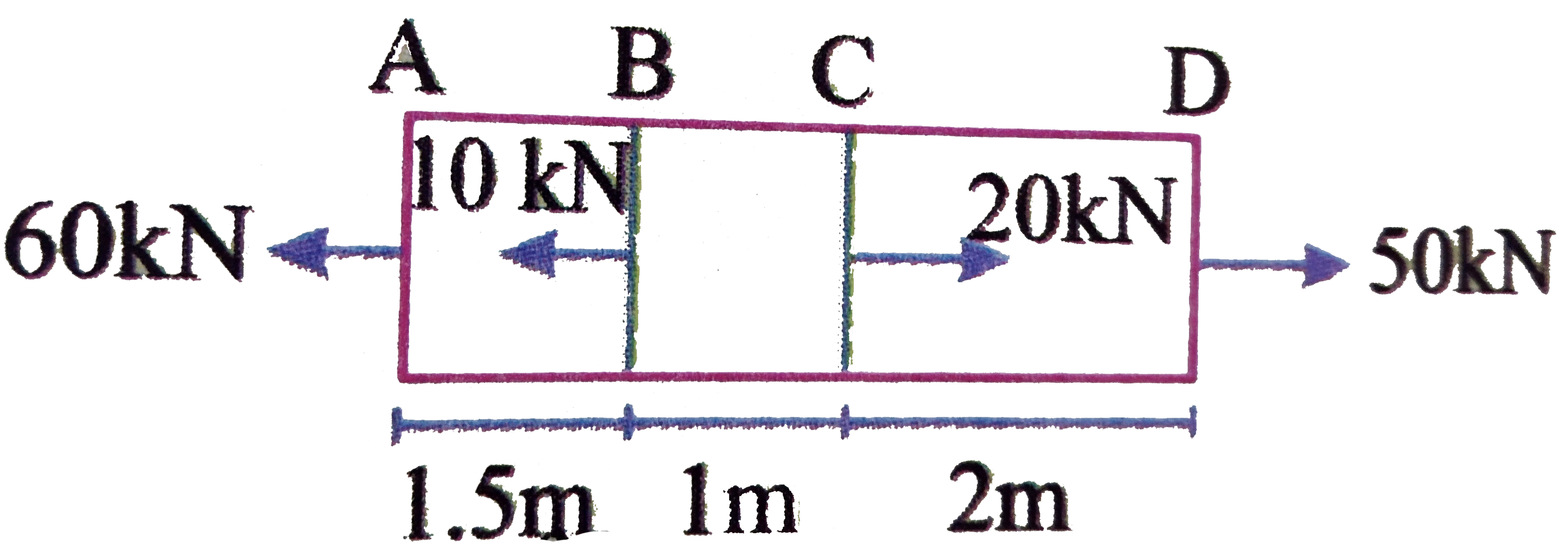
View SolutionTwo wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?

View SolutionA steel rod of cross sectional area 4cm2andlength 2m shrinks by 0.1 cm as the temperature decreases in night. If the rod is clamped at both ends during the day horus, find the tension developed in it during night hours. Young modulus of steel =1.9×10611 nm^-2
View Solution
