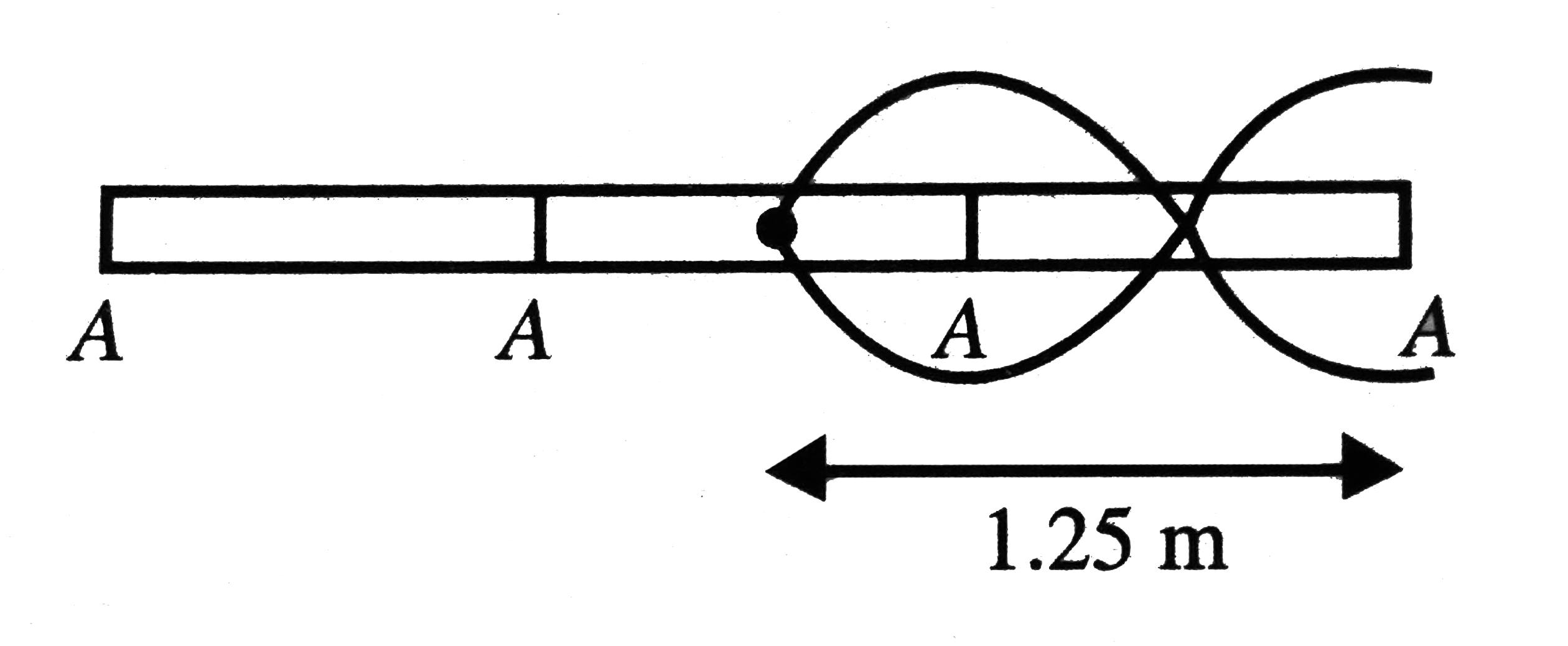
A steel rod $2.5 m$ long is rigidly clamped at its centre $C$ and longitudinal waves are set up on both sides of $C$ by rubbing along the rod . Young's modulus for steel $= 2 \times 10^{11} N / m^{2}$ , density of steel $= 8000 k g / m^{3}$

If two antinodes are observed on either side of $C$ , the frequency of the node in which the rod is vibrating will be

A

$1000 H z$

B

$3000 H z$

C

$7000 H z$

D

$1500 H z$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Velocity of the longitudinal waves in the rod
$v = \sqrt{Y / d} = \sqrt{2 \times 10^{11} / 8000} = 5000 m / s$
The wavelength of the wire for the mode of vibration in which $2$ antinodes occur is
$λ = \frac{1.25}{(3 / 4)} = \frac{5}{3} m$
Hence frequency of vibration
$n = \frac{V}{λ} = \frac{5000}{5 / 3} H z = 3000 H z$

|

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A steel rod $2.5 m$ long is rigidly clamped at its centre $C$ and longitudinal waves are set up on both sides of $C$ by rubbing along the rod . Young's modulus for steel $= 2 \times 10^{11} N / m^{2}$ , density of steel $= 8000 k g / m^{3}$

If the clamp of the rod be shifted to its end $A$ and totally four antinodes are observed in the rod when longitudinal waves are set up in it , the frequency of vibration of the rod in this mode is
A $500 H z$
B $2500 H z$
C $3500 H z$
D $1500 H Z$
Question 2 - Select One
A steel rod $2.5 m$ long is rigidly clamped at its centre $C$ and longitudinal waves are set up on both sides of $C$ by rubbing along the rod . Young's modulus for steel $= 2 \times 10^{11} N / m^{2}$ , density of steel $= 8000 k g / m^{3}$

If the amplitude of the wave at the antinode , when it is vibrating in its fundamental mode is $2 \times 10^{- 6} m$ , the maximum velocity of a steel particle in its vibration is
A $1.25 \times 10^{- 2} m / s$
B $1.25 \times 10^{- 3} m / s$
C $1 m / s$
D $0.12 m / s$
Question 3 - Select One
If the young's modulus of the material of the rod is $2 \times 10^{11} N / m^{2}$ and its density is $8000 k g / m^{3}$ then the time taken by a sound wave to traverse 1m of the rod will be
A $10^{- 4} s$
B $2 \times 10^{- 4} s$
C $10^{- 2} s$
D $2 \times 10^{- 2} s$

CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Comprehension

Home
Ask Doubt
Profile