A stone of mass 1 kg tied to a light inextensible string of lenth L=103m, whirling in a circular path in a vertical plane. The ratio of maximum tension to the minimum tension in the string is 4. If g is taken to be 10ms−2, the speed of the stone at the highest point of the circle is
10ms−1
5√2ms−1
10√3ms−1
20ms−1
The correct Answer is:A
To find the speed of the stone at the highest point of its circular motion, we need to analyze the forces acting on the stone at both the highest and lowest points of the circular path. Let's break down the solution step by step.
Step 1: Identify the Forces at the Highest Point
At the highest point of the circular path, the forces acting on the stone are:
- The tension in the string (T_a) acting downward.
- The weight of the stone (mg) acting downward.
The net force towards the center of the circle (centripetal force) is given by:
Ta+mg=mv2aL
where:
- m=1kg (mass of the stone)
- g=10m/s2 (acceleration due to gravity)
- L=103m (length of the string, which is the radius of the circular path)
- va is the speed at the highest point.
Step 2: Identify the Forces at the Lowest Point
At the lowest point of the circular path, the forces acting on the stone are:
- The tension in the string (T_b) acting upward.
- The weight of the stone (mg) acting downward.
The net force towards the center of the circle is given by:
Tb−mg=mv2bL
where vb is the speed at the lowest point.
Step 3: Set Up the Equations
From the equations derived in Steps 1 and 2, we can express the tensions:
1. From the highest point:
Ta=mv2aL−mg
Ta=1⋅v2a103−1⋅10
Ta=3v2a10−10
2. From the lowest point:
Tb=mv2bL+mg
Tb=1⋅v2b103+1⋅10
Tb=3v2b10+10
Step 4: Use the Ratio of Tensions
We are given that the ratio of maximum tension to minimum tension is 4:
TbTa=4
Substituting the expressions for Ta and Tb:
3v2b10+103v2a10−10=4
Step 5: Cross Multiply and Simplify
Cross-multiplying gives:
10(3v2b+100)=4(3v2a−100)
Expanding both sides:
30v2b+1000=12v2a−400
Rearranging gives:
12v2a−30v2b=1400
Step 6: Use Conservation of Energy
Using conservation of energy between the highest and lowest points:
12mv2b=12mv2a+mg(2L)
Substituting values:
12v2b=12v2a+10⋅(2⋅103)
12v2b=12v2a+2003
Step 7: Solve the System of Equations
Now we have two equations:
1. 12v2a−30v2b=1400
2. 12v2b=12v2a+2003
From the second equation, express v2b:
v2b=v2a+4003
Substituting this into the first equation:
12v2a−30(v2a+4003)=1400
12v2a−30v2a−4000=1400
−18v2a=5400
v2a=300
va=√300=10√3m/s
Final Answer
The speed of the stone at the highest point of the circle is:
va=10√3m/s
At the highest point of the circular path, the forces acting on the stone are:
- The tension in the string (T_a) acting downward.
- The weight of the stone (mg) acting downward.
Ta+mg=mv2aL
where:
- m=1kg (mass of the stone)
- g=10m/s2 (acceleration due to gravity)
- L=103m (length of the string, which is the radius of the circular path)
- va is the speed at the highest point.
At the lowest point of the circular path, the forces acting on the stone are:
- The tension in the string (T_b) acting upward.
- The weight of the stone (mg) acting downward.
Tb−mg=mv2bL
where vb is the speed at the lowest point.
From the equations derived in Steps 1 and 2, we can express the tensions:
1. From the highest point:
Ta=mv2aL−mg
Ta=1⋅v2a103−1⋅10
Ta=3v2a10−10
Tb=mv2bL+mg
Tb=1⋅v2b103+1⋅10
Tb=3v2b10+10
We are given that the ratio of maximum tension to minimum tension is 4:
TbTa=4
3v2b10+103v2a10−10=4
Cross-multiplying gives:
10(3v2b+100)=4(3v2a−100)
Expanding both sides:
30v2b+1000=12v2a−400
Rearranging gives:
12v2a−30v2b=1400
Using conservation of energy between the highest and lowest points:
12mv2b=12mv2a+mg(2L)
Substituting values:
12v2b=12v2a+10⋅(2⋅103)
12v2b=12v2a+2003
Now we have two equations:
1. 12v2a−30v2b=1400
2. 12v2b=12v2a+2003
v2b=v2a+4003
12v2a−30(v2a+4003)=1400
12v2a−30v2a−4000=1400
−18v2a=5400
v2a=300
va=√300=10√3m/s
The speed of the stone at the highest point of the circle is:
va=10√3m/s
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
If a stone of mass 2 kg is tied to a inextensible string of length 2 m is whirling in a circular path of radius L in vertical plane at uniform speed. If the ratio of maximum tension to minimum tension in the string is 3. Then, the speed of stone at highest point of circle is ...... m/s
View SolutionA stone of mass m tied to a light inextensible sting of length L(=103m) is whirling in a circular path of radius L in a verticle plane. If the ratio of the maximum to the minimum tension is four, find the speed of the stone at the highest point of the circle.
View Solution
Knowledge Check
A stone of mass 1kg tied to a light inextensible sstring of length L=10m is whirling in a circular path of radius L in vertical plane. If the ratio of the maximum tension in the string to the minimmum tension in the string is 4 and if g is taken to be 10ms−2 , the speed of the stone at the highest point of the circle is.
A10ms−1B5√2ms−1C10√3DNone of theseA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
A20m/sB10√3m/sC5√2m/sD10m/sA stone of mass 1 kg tied to a light inextensible string of length L=53m, is whirling in a vertical circle of radius L. If the ratio of the maximum and minimum tension in the string is 4 and g=10m/s2, the speed of stone at the highest point of the circle is
A5m/sB5√3m/sC5√2m/sD10m/s
Consider a stone of mass 1 kg tied to a light inextensible string and whirling in a vertical circular path. The length of the string is fount to be 104 m. It is also fount that theratio of the maximum to minimum tension is 3. The find the speed of the stone at the highest point of the circle in ms−1. (Take g=10ms−2)
View SolutionA stone of 1 kg tied up with 10/3 m long string rotated in a vertical circle. If the ratio of maximum and minimum tension in string is 4 then speed of stone at highest point of circular path will be ( g=10ms2)
View SolutionA stone of mass 0.5 kg tied with a string of length 1 metre is moving in a circular path with a speed of 4 m/sec. The tension acting on the string in Newton is-
View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
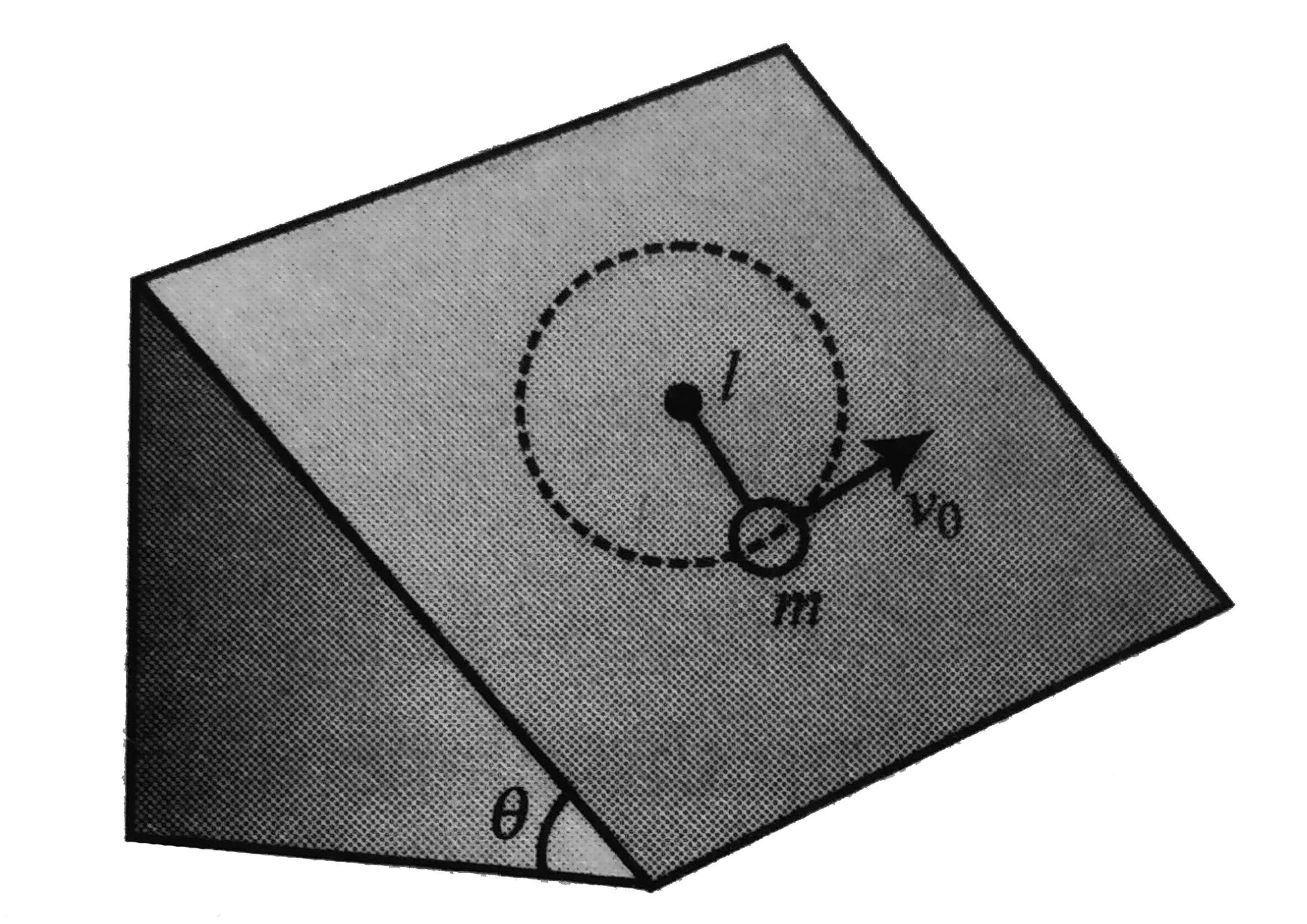
The speed of the bob at the highest point on the circle is
View SolutionStone of mass 1 kg tied to the end of a string of length 1m , is whirled in horizontal circle with a uniform angular velocity 2rads−1. The tension of the string is (in newton)
View Solution
