A stone of mass m is tied to one end of a wire of length L. The diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle θ with the vertical. If Young's modulus of the wire is Y, then the increase in the length of the wire is
4mglπD2Y
4mglπD2Ysinθ
4mglπD2Ycosθ
4mglπD2Ytanθ
The correct Answer is:C
The situation is as shown in the figure. For vertical equilibrium of stone
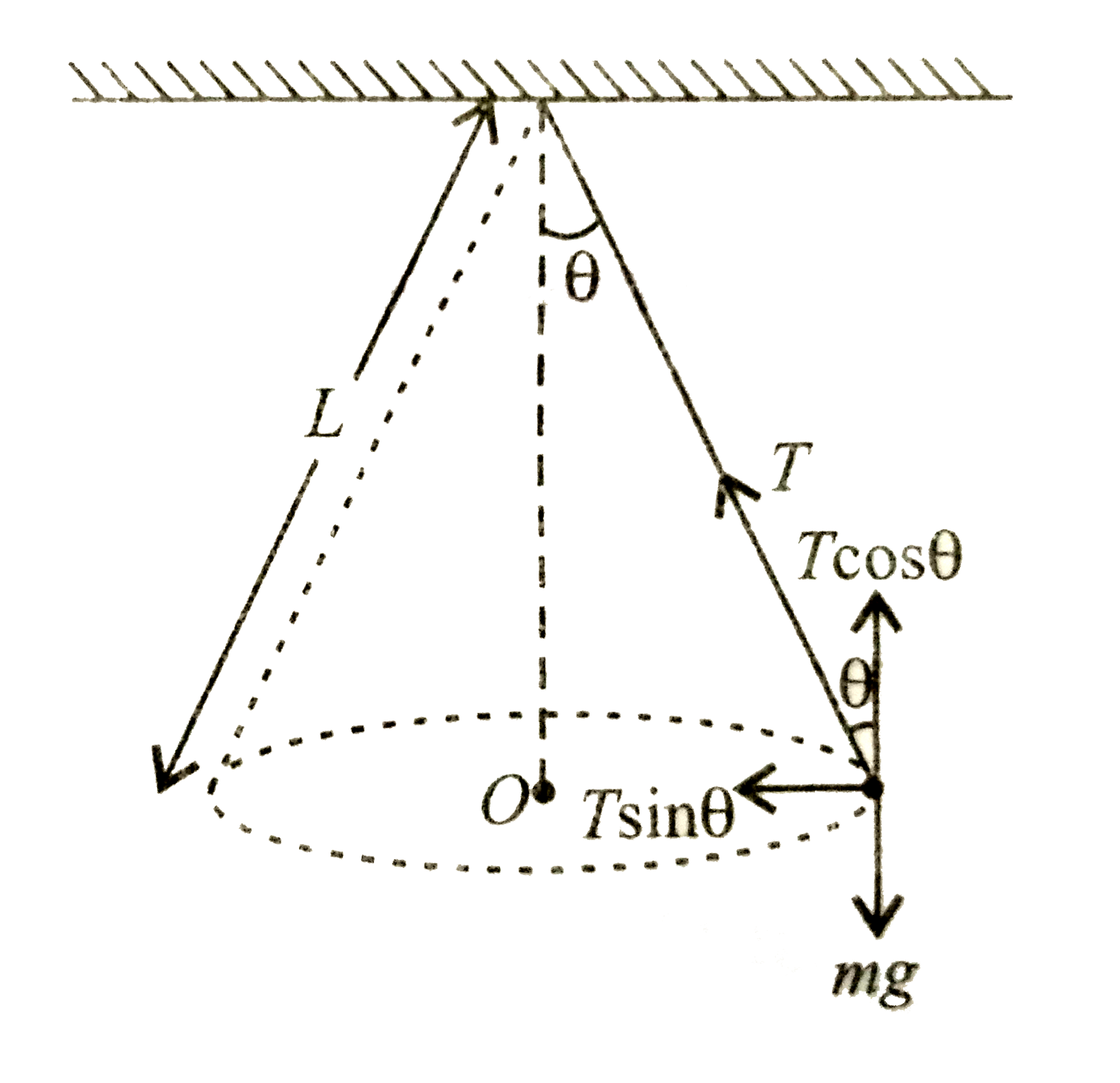
Tcosθ=mgorT=mgcosθ .....(i)
As Y=TALΔL
∴ΔL=TLAY (Using (i))
=mgLcosθ(πD2/4)Y=4mglπD2Ycosθ
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Applications Of Elastic Behaviour Of Materials
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Higher Order Thinking Skills
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Stress-Strain Curve
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A stone of 0.5 kg mass is attached to one end of a 0.8 m long aluminium wire of 0.7 mm diameter and suspended vertically . The stone is now rotated in a horizontal plane at a rate such that the wire makes an angle of 85∘ with the vertical . find the increase in the length of the wire . The Young's modulus of aluminium = 7×1010Nm−2,sin85∘=0.9962,cos85∘=0.0872
View SolutionA stone of mass m is attached to one end of a wire of cross-sectional area A and Young's modulus Y. The stone is revolved in a horizontal circle at a speed such that the wire makes an angle θ with the vertical. The strain produced in the wire will be
View Solution
Knowledge Check
A stone of mass m tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is Y, Then the increase in the length of the wire is
A4mgLπD2YB4mgLπD2YsinθC4mgLπD2YcosθD4mgLπD2YtanθAn iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is
A0.2 mmB0.5 mmC2 mmD1 mmA uniform wire of radius r and length L hanging vertically and fixed at its upper ends, is attached to a weight at its lower end. If Young's modulus for the material of the wire is Y, the extension is
Ainversely proportional to Y.Binversely proportional to r2.Cdirectly proportional to L.Dinversely proportional to r.
A stone of mass 1kg is attached to one end of a 1.4m long aluminimum wire 0.4mm in diameter and stone is rotated in a horizontal plane at a rate such that the wire makes an angle of 60∘ with the vertcal. Take Young's modulus of aluminium =7×1010N/m2. If increase in length of the wire is 2Δlπmm then value of Δl is :
View SolutionWhen a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L+l). The elastic potential energy stored in the extended wire is
View SolutionA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
View SolutionA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
View SolutionA wire of mass m and length l is suspended from a ceiling. Due to its own wieght it elongates, consider cross-section are of wire as A ans Young's modulus of material of wire as Y. Th eelongation in the wire is
View Solution
