A stone tied to a string of length L is whirled in a vertical circle with the other end of the string at the centre. At a certain instant of time the stone is at lowest position and has a speed u . Find the magnitude of the change in its velocity as it reaches a position, where the string is horizontal.
√2(u2−gl)
√u2−gl
u−√u2−2gl
√2gl
The correct Answer is:A
Using conservation of mechanical energy at initial and final position.
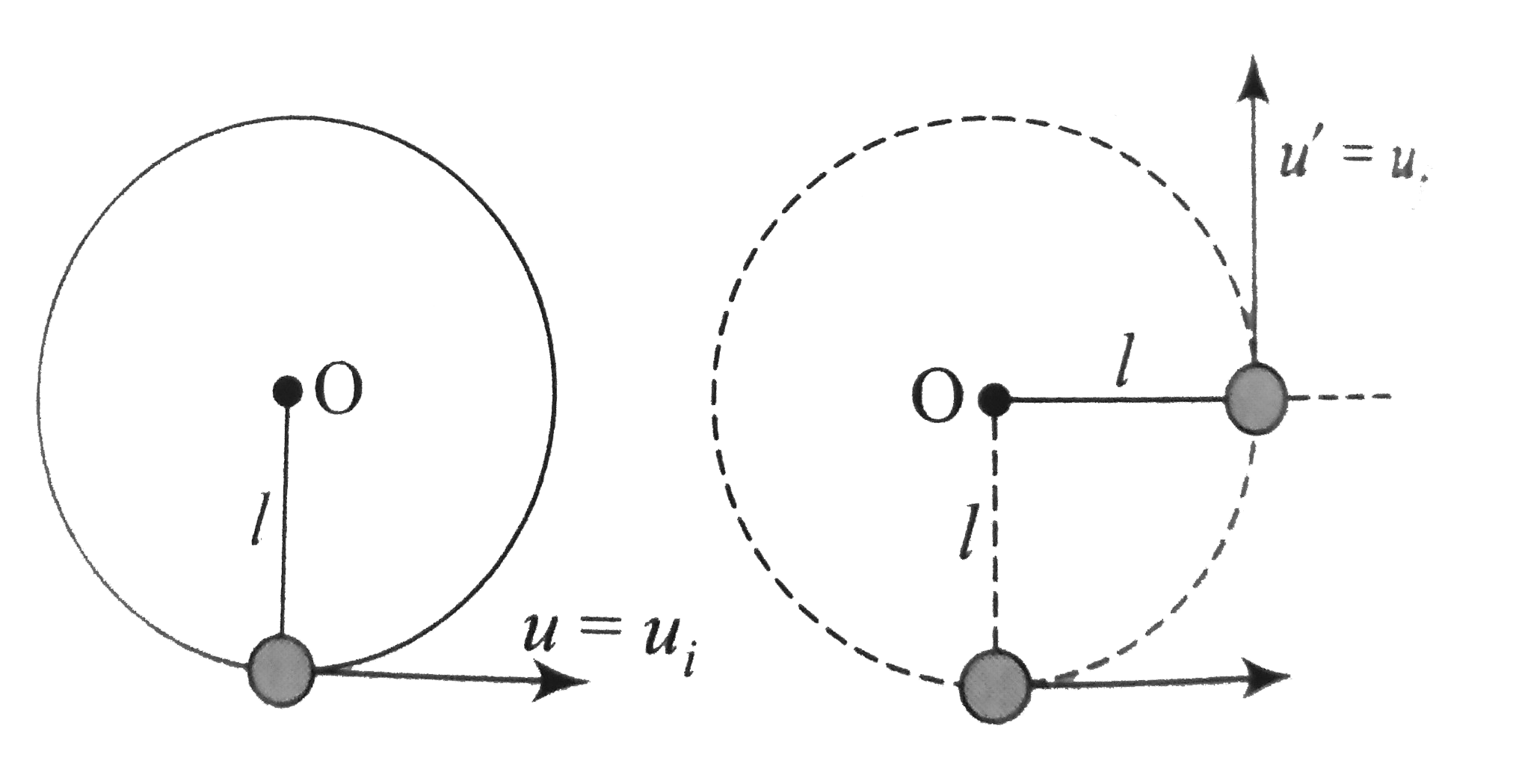
Δk+ΔU=0
(12μ'2−12μ2)+(mgl)=0
or u'2=u2−2gl
or u'=√u2−2gl (i)
So, the magnitude of change in velocity
Δ→u=→uf−→ui=→uf+(→ui)
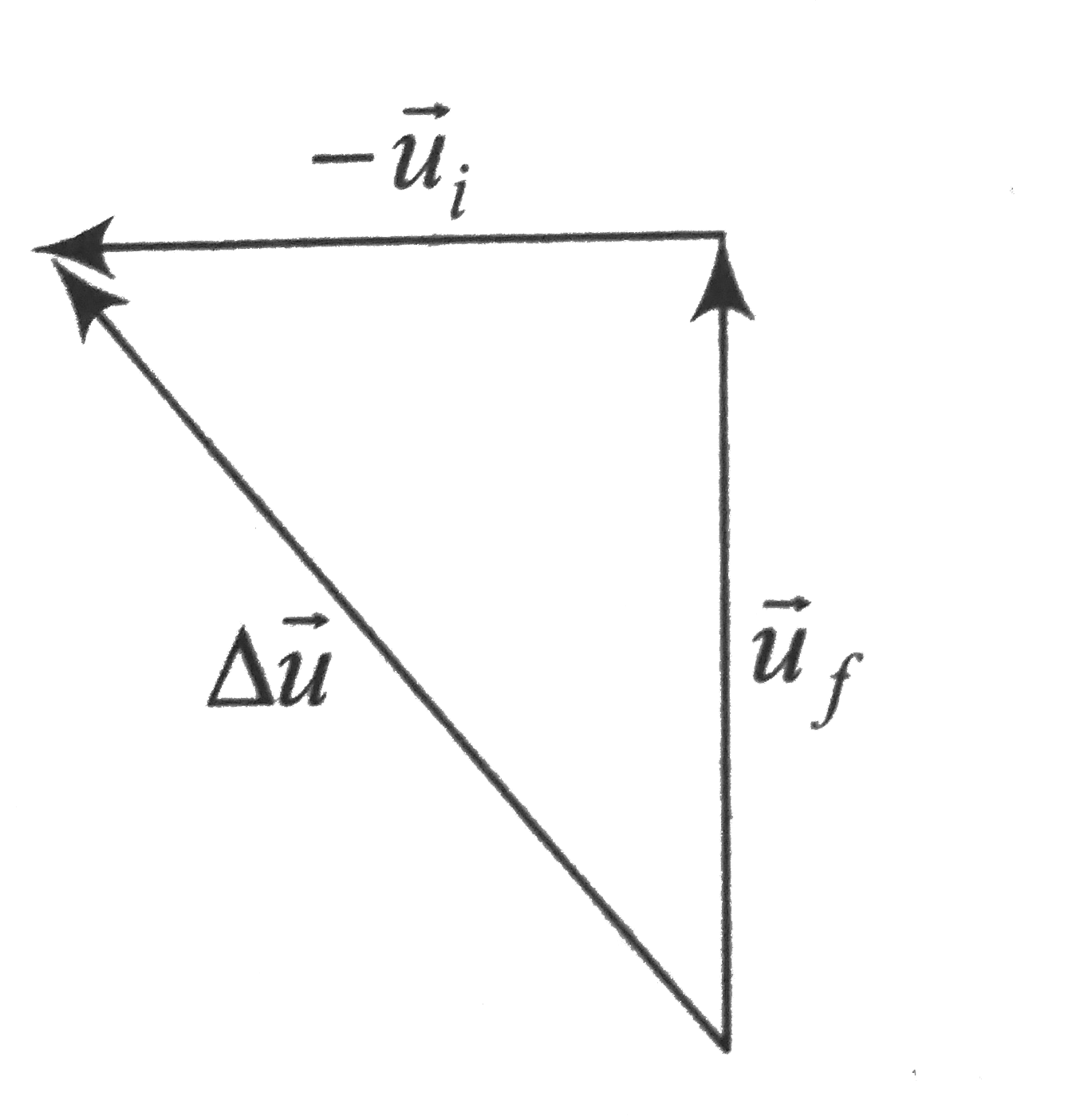
|Δ→u|=√u'2+u2=√(u2−2gh)+u2
=√2(u2−gl).
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - AIIMS Questions
20 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
A stone tied to a string of length L is whirled in a vertical circle with the ofter end of the string at the centre . At a certin instant of time , the stone is at its lowest position , and has a speed is , the magintube of the change in its velocity as it reached a positive when the string is horizontal is
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View Solution
Knowledge Check
A stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
A√u2−2gLB√2gLC√u2−gLD√2(u2−gL)A stone tied to a string of length L is whirled in a vertical circle, with the other end of the string at the centre. At a certain instant of time, the stone is at its lowest position, and has a speed u. The magnitude of change in its velocity as it reaches a position, where the string is horizontal is
A√u2−2gLB√2gLC√u2−gLD√2(u2−gL)A stone is tied to a string of length l and is whirled in a vertical circle with the other end of the string as the centre. At a certain instant of time, the stone is at its lowest position and has a speed u. The magnitude of the change in velocity as it reaches a position where the string is horizontal (g being acceleration due to gravity) is
A√2(u2−gl)B√u2=glCu−√u2=2glD√2gl
A stone of a mass m tied to a string of length /is rotated in a circle with the other end of the string as the centre. The speed of the stone is V. If the string breaks, the stone will
View SolutionA stone is tied to the end of a string of length 1 and whirled in a horizental circle. When the string breaks then stone
View SolutionIf a bodyy is tied to a string and whirled in vertical circle, then the tension in the string at the highest position is
View SolutionA pendulum bob is rotated in a vertical circle with one end of string of length l fixed at a position . At a certain instant bob is at its lowest position and is moving with speed u . Calculate the magnitude of change in velocity when string becomes horizontal for a moment .
View SolutionA stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
View Solution