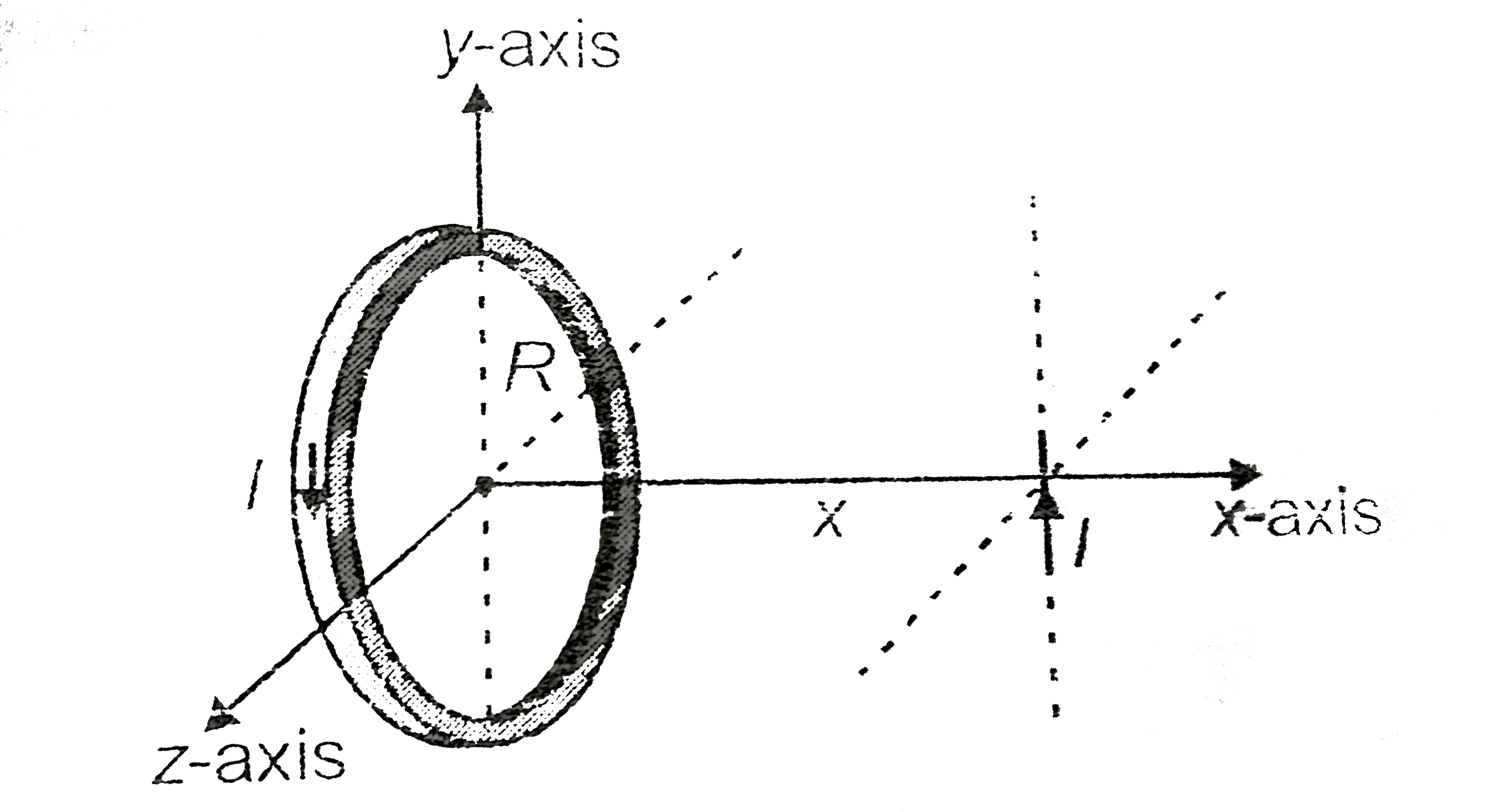
A straight current carrying conductor is kept along the axis of circular loop carrying current. The force exerted by the straight conductor on the loop is
Perpendicular to the plane of the loop
In the plane of the loop, away from the center
In the plane of the loop, towards the center
Zero.
To solve the problem of the force exerted by a straight current-carrying conductor on a circular loop carrying current, we can follow these steps:
1. Understand the Configuration:
- We have a straight current-carrying conductor placed along the axis of a circular loop. The axis of the circular loop is perpendicular to the plane of the loop.
2. Determine the Magnetic Field:
- A straight current-carrying conductor generates a magnetic field around it. For a straight conductor, the magnetic field (B) at a distance (r) from it is given by the formula:
B=μ0I12πr
where I1 is the current in the straight conductor and μ0 is the permeability of free space.
3. Analyze the Circular Loop:
- The circular loop carries its own current (let's denote it as I2). The magnetic field produced by the straight conductor will affect the current in the loop.
4. Force on the Loop:
- The force on a current-carrying conductor in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
where I is the current in the loop, L is the length of the conductor in the magnetic field, B is the magnetic field strength, and θ is the angle between the direction of the current and the magnetic field.
5. Evaluate the Angle:
- In this case, the magnetic field generated by the straight conductor is parallel to the plane of the circular loop. Therefore, for any small element of the loop (dL), the angle θ between the magnetic field and the current element is 0 degrees.
6. Calculate the Force:
- Since sin(0)=0, the force exerted on the loop by the straight conductor becomes:
F=I2⋅dL⋅B⋅sin(0)=0
- Thus, the total force exerted by the straight conductor on the loop is zero.
7. Conclusion:
- Therefore, the force exerted by the straight conductor on the circular loop is zero.
Final Answer:
The force exerted by the straight conductor on the loop is zero.
- We have a straight current-carrying conductor placed along the axis of a circular loop. The axis of the circular loop is perpendicular to the plane of the loop.
- A straight current-carrying conductor generates a magnetic field around it. For a straight conductor, the magnetic field (B) at a distance (r) from it is given by the formula:
B=μ0I12πr
where I1 is the current in the straight conductor and μ0 is the permeability of free space.
- The circular loop carries its own current (let's denote it as I2). The magnetic field produced by the straight conductor will affect the current in the loop.
- The force on a current-carrying conductor in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
where I is the current in the loop, L is the length of the conductor in the magnetic field, B is the magnetic field strength, and θ is the angle between the direction of the current and the magnetic field.
- In this case, the magnetic field generated by the straight conductor is parallel to the plane of the circular loop. Therefore, for any small element of the loop (dL), the angle θ between the magnetic field and the current element is 0 degrees.
- Since sin(0)=0, the force exerted on the loop by the straight conductor becomes:
F=I2⋅dL⋅B⋅sin(0)=0
- Thus, the total force exerted by the straight conductor on the loop is zero.
- Therefore, the force exerted by the straight conductor on the circular loop is zero.
The force exerted by the straight conductor on the loop is zero.
Topper's Solved these Questions
Similar Questions
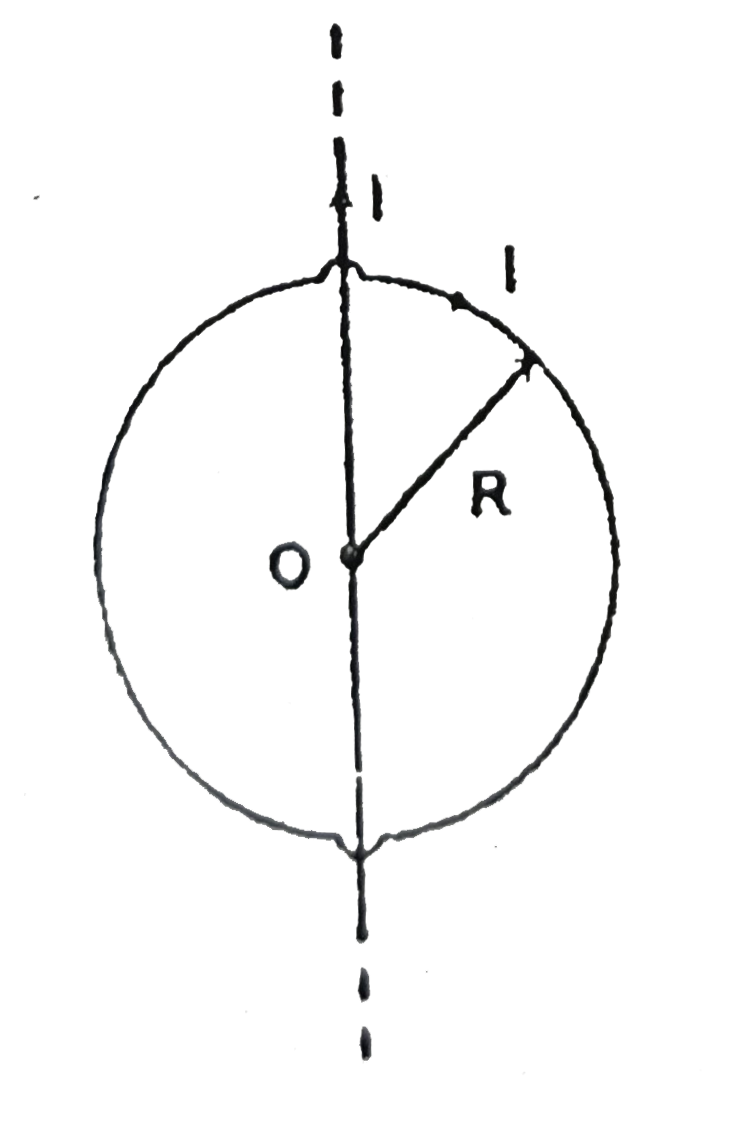
A short current carrying conductor is placed perpendicular to the axis of a current carrying ring as shown. The direction of force acting of the conductor is
View SolutionA circular conducting loop of radius R carries a current I. Another straight infinite conductor carrying current I passes through the diameter of this loop as shown in the figure. The magnitude of force exerted by the straight conductor on the loop is
View Solution
Knowledge Check
A straight current carrying conductor is kept along the axis of circular loop canying current. The force exerted by the straight conductor on the loop is
Aperpendicular to the plane of the loopBin the plane of the loop, away from the centerCin the plane of the loop, towards the centerDzeroA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
Awill exert an inward force on the circular loopBwill exert an outward force on the circular loopCwill not exert any force on the circular loopDwill exert a force on the circular loop parallel to itself.A current-carrying, straight wire is kept along the axis of a square loop carrying a current.The straight wire
Awill exert an inward force on the square loopBwill exert an outward force on the square loopCwill not exert any force on the square loopDwill exert a force on the square loop parallel to itself.
A long, straight conductor lies along the axis of a ring. Both carry current I. The force on the ring is proportional to
View SolutionAssertion (A): Magnetic field due to a straight current carrying conductor is in the form of circular loops around it.
Reason (R): The magnetic field due to a current carrying conductor is weak at near points from the conductor.
View SolutionCurrent carrying circular loop acts as
View SolutionA straight wire carrying a current i1 amp runs along the axis of a circular current i2 amp. Then the force of interaction between the two current carrying conductors is
View SolutionAn electron is projected along the axis of a circular conductor carrying some current. Electron will experience force
View Solution
