A straight rigid rod of mass M and length L lies on a smooth horizontal table. Taking the co-ordinate axes as shown in the figure and assuming an average force <F> acting for a small time interval (△t), at the end A, making an angle 30∘ with the X-axis, Based on the above passege, answer the following questions.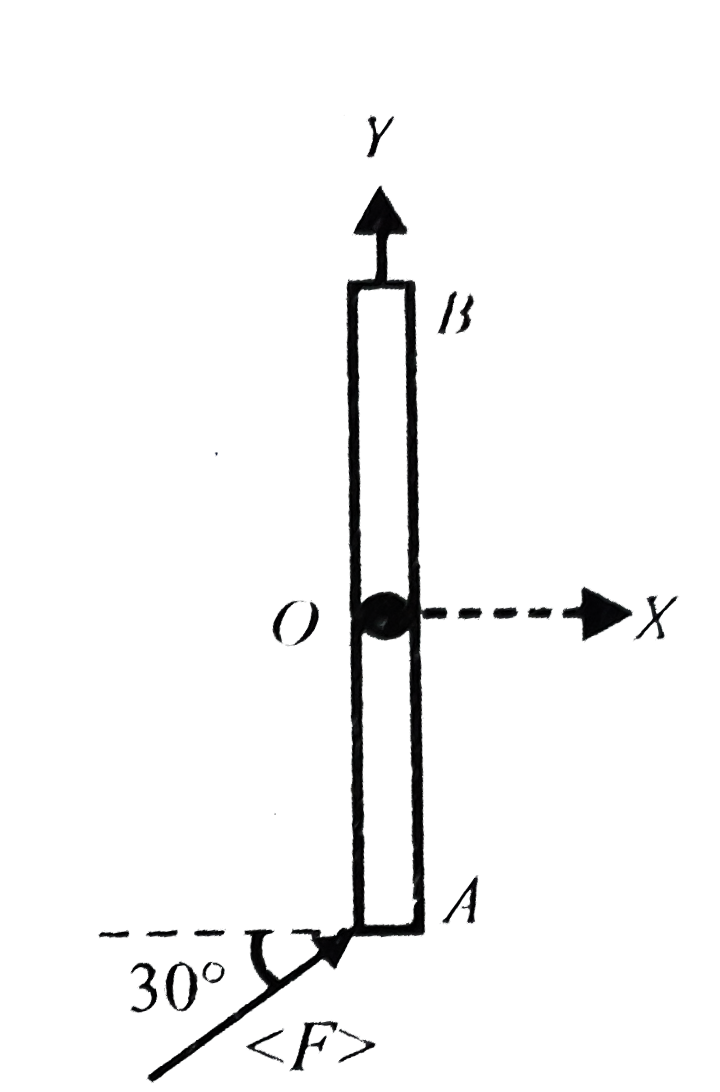
Linear velocity of the CM of rod is
<F>(△t)2m/(2m)(√3ˆi+ˆj)
<F>(△t)2m/(2m)(√5ˆi+2ˆj)
<F>(△t)2m/m(√3ˆi+ˆj)
<F>(△t)2m/m(√5ˆi+ˆj)
The correct Answer is:A
Jx=MVξmpliesVx=Jcos30∘M
Jy=MVy⇒Vy=Jcos30∘M
Hence →v=vxˆi=vyˆj
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
A straight rigid rod of mass M and length L lies on a smooth horizontal table. Taking the co-ordinate axes as shown in the figure and assuming an average force <F> acting for a small time interval (△t), at the end A, making an angle 30∘ with the X-axis, Based on the above passege, answer the following questions.
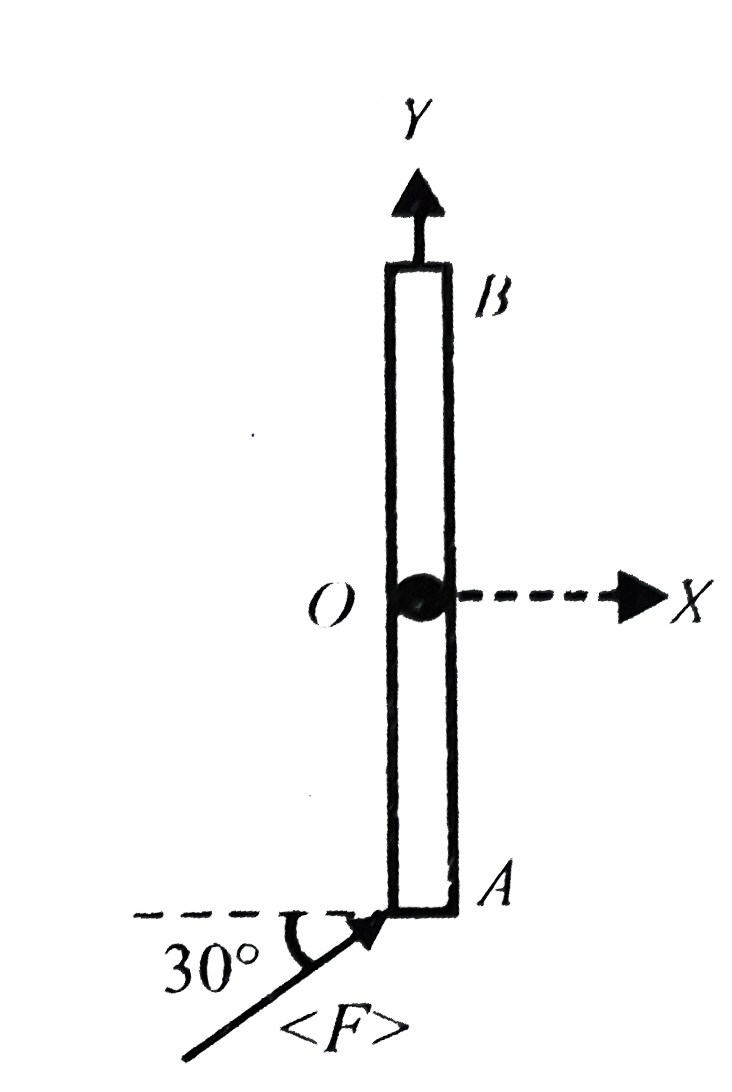
Angular velocity of rod about O is
View SolutionA straight rigid rod of mass M and length L lies on a smooth horizontal table. Taking the co-ordinate axes as shown in the figure and assuming an average force <F> acting for a small time interval (△t), at the end A, making an angle 30∘ with the X-axis, Based on the above passege, answer the following questions.
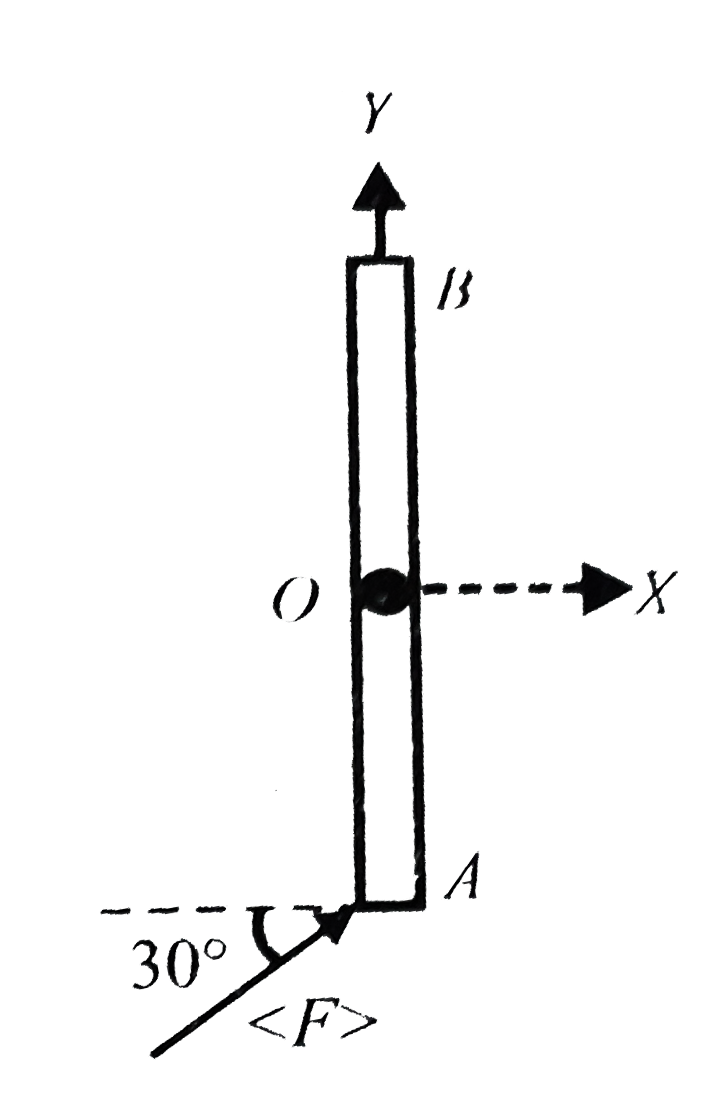
The angular impulse, due to the force about O, is
View SolutionA uniform rod of mass m, length l is placed over a smooth horizontal surface along y -axis and is at rest as shown in figure. An impulsive force F is applied for a small time Δt along x-direction at point A. The x-coordinte of end A of the rod when the rod becomes parallel to x-axis for the first is (in itially the coordinates opf centre of mass of the rod is (0,0).

View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionTwo blocks of masses 'M' and 'm' are placed on one another on a smooth horizontal surface as shown in the figure. The force 'F' is acting on the mass 'M' horizontally during time interval 't'. Assumings no relative sliding between the blocks, The work done by friction on the blocks is
View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA rod of length 10 meter has one end on smooth floor and the other end on smooth wall is released from the rest the position shown in figure. When the rod makes an angle of 37∘ with the horizontal, answer the following:

The velocity of centre of mass of rod is :
View SolutionA thin uniform copper rod length l and mass m rotates unifomly with an angular velocity ω about a vertical axis passing through one of its ends as shown in the figure. Young's modulus of copper is Y. Breaking stress is σmax, cross sectional area of rod is A and density of rod is uniform. Based on above information, answer the following questions
The maximum angular velocity with which the rod can rotate so that is won't break, is

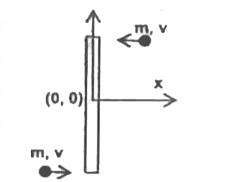
View SolutionA rigid uniform rod of mass M and length L is placed along the Y-axis on a smooth horizontal surface with its centre at the origin. Two particles , each of mas m(=M/12) hits simultaneously , at the two ends with equal speed v as shown in the figure. The collision is completely inelastic.
(i) Find the angular velocity of the system after the collision.
(ii) Two particles of mass 2m and m are placed respectively at ( L/2,0) and (−L/2,0). Calculate the time when the rod hits these particles.
View Solution
