A straight rod AB of mass and length is placed on a frictionless horizontal surface. A force having constant magnitude F and a fixed direction start acting at the end A. The rod is initially prependicular to the force. The initial acceleration of end B is
zero
None of these

(downward)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2 Subjective
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A straight rod AB of mass M and length L is placed on a frictionless horizontal surface. A horizontal force having contstant magnitude F and fixed direction starts acting at the end A. The rod is initially perpendicular to the force. Find the initial acceleration of end B.
View SolutionA rod of mass M and length L is placed on a smooth horizontal surface. It is hinged at one end so that it can rotate freely in a horizontal circle about this end. There exists a uniform magnetic field →B perpendicular, into the horizontal surface everywhere. The strength of magnetic field starts varying as B=B0t.
(i) Find the torque acting on the rod about its hinged end.
(ii) Find the reaction produced at hinge at t = 0.
(A charge Q is distributed uniformaly on the rod)
View Solution
Knowledge Check
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
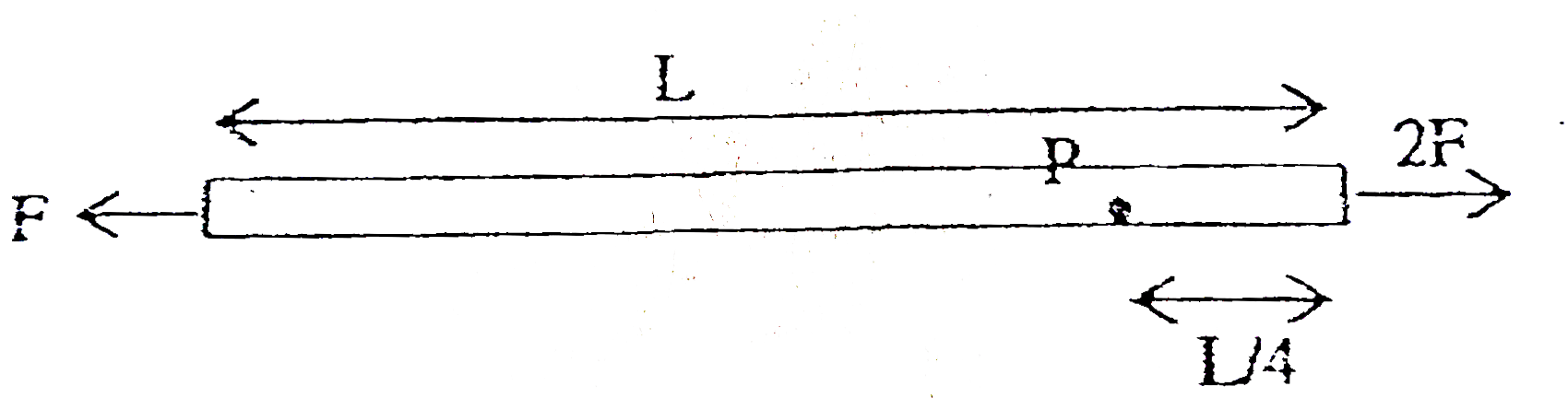 AFB3FC5F4D7F4
AFB3FC5F4D7F4A straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'l' from that end is
AFlBLFlC(1−lL)FD(1+lL)FA uniform rod of mass M and length L, area of cross section A is placed on a smooth horizontal surface. Forces acting on the rod are shown in the digram

Total elastic potential energy stored in the rod is :A7F2L6AYB11F2L6AYC5F2L6AYD3F2L2AY
A thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.
View SolutionA uniform rod of length L rests on a frictionless horizontal surface. The rod is pivoted about a fixed frictionless axis at one end. The rod is initially at rest. A bulled travelling parallel to the horizontal surface and perpendicular to the rod with speed v strikes the rod at its centre and becomes embedded in it. the mass of the bullet is one-sixth the mass of the rod.
(a). What is the final angular velocity of the rod?
(b). What is the ratio of the kinetic energy of the system after the collision to the kinetic energy of te bullet the o collision?
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'I from that end is 9
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View Solution