A stress of 1 kg mm−2 is applied to a wire of which Young's modulus is 1011Nm−2 and 1.1×1011Nm−2. Find the percentage increase in length.
The correct Answer is:0.0098%
To solve the problem of finding the percentage increase in length of a wire when a stress of 1 kg/mm² is applied, and given that the Young's modulus is 1011N/m2, we can follow these steps:
Step 1: Convert Stress to SI Units
The given stress is 1kg/mm2. We need to convert this to N/m2 (Pascals) for consistency with the Young's modulus units.
1 kg = 9.8 N (approximately, due to gravity), and 1mm2=10−6m2.
Thus,
Stress=1kg/mm2=1×9.8N/(1×10−6m2)=9.8×106N/m2.
Step 2: Use Young's Modulus to Find Strain
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain.
Rearranging this gives:
Strain=StressY.
Substituting the values:
Strain=9.8×106N/m21011N/m2=9.8×10−5.
Step 3: Relate Strain to Change in Length
Strain is also defined as the change in length (ΔL) divided by the original length (L):
Strain=ΔLL.
Step 4: Calculate Percentage Increase in Length
To find the percentage increase in length, we multiply the strain by 100:
Percentage Increase=Strain×100=9.8×10−5×100=9.8×10−3or0.0098(in percentage).
Final Answer
The percentage increase in length of the wire is approximately 0.0098%.
---
The given stress is 1kg/mm2. We need to convert this to N/m2 (Pascals) for consistency with the Young's modulus units.
Stress=1kg/mm2=1×9.8N/(1×10−6m2)=9.8×106N/m2.
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain.
Rearranging this gives:
Strain=StressY.
Strain=9.8×106N/m21011N/m2=9.8×10−5.
Strain is also defined as the change in length (ΔL) divided by the original length (L):
Strain=ΔLL.
To find the percentage increase in length, we multiply the strain by 100:
Percentage Increase=Strain×100=9.8×10−5×100=9.8×10−3or0.0098(in percentage).
The percentage increase in length of the wire is approximately 0.0098%.
Topper's Solved these Questions
Similar Questions
A stress of 1kg/mm2 is applied on a wire. If the modulus of elasticity of the wire is 1010dyne/cm2, then the percentage increase in the length of the wire will be
View SolutionA steel rod of length l1=30cm and two identical brass rod of length l2=20cm each support a light horizontal platform as shown in Fig. Cross-sectional area of each of the three rods is A=1cm2. A vertically downward force F=5000N is applied on the platform. Young's modulus of elasticity for steel Ys=2×1011Nm−2 and brass Yb=1×1011Nm−2. Find stress (in MPa) developed in a. Steel rod b. Brass rod
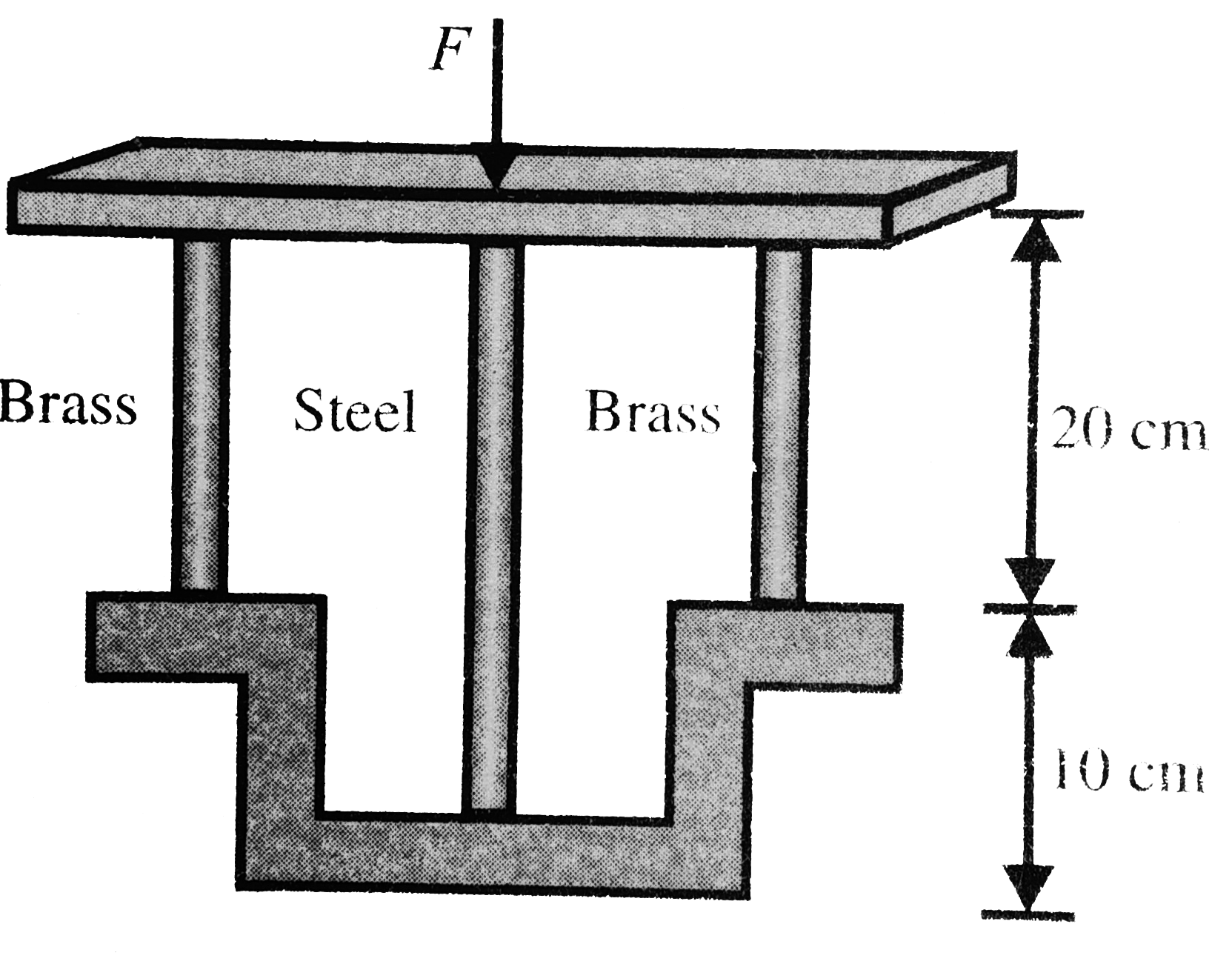
View Solution
Knowledge Check
A stress of 1 kg wt/mm2 is applied to a wire whose Young's modulus is 1012dyne/cm2. The percentage increase in its length is
A0.98B98×10−4C9.8×10−6D9.8×10−5A stress of 3.18×108Nm−2 is applied to a steel rod of length 1m along its length, its Young's modulus is 2×1011Nm−2. Then the elongation produced in the rod (in mm) is
A3.18B6.36C5.18D1.59A stress of 3.18×108 Nm−2 is applied to a steel rod of length 1 m along its length, its Young's modulus is 2×1011Nm−2. Then the elongation in mm produced in the rod, is
A3.18B6.36C5.18D1.59
Longitudinal stress of 1kg/mm2 is applied on a wire. The percentage increase in length is (Y=1011N/m2)
View SolutionSteel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are 2×1011Nm2 and 1.2×1011Nm2. The ratio of increase in length is
View SolutionThe area of cross-section of a wire of length 1.1 meter is 1mm2. It is loaded with 1 kg. if young's modulus of copper is 1.1×1011N/m2 then the increase in length will be (if g=10m/s2)-
View SolutionAn iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is
View SolutionA 4m long copper wire of cross sectional are a1.2cm2 is strechted by a force of 4.8×103N.
if Young's modulus for copper is Y=1.2×1011M/m2 , the increases in length of wire and strain energy per unit volume are
View Solution
