A string fastened at both ends has successive resonances with wavelengths of 0.1 m for mth harmonic and 0.08 m for (m+1)th harmonic.
The value of m is
3
4
5
6
The correct Answer is:B
To solve the problem, we need to find the value of m given the wavelengths for the m-th and (m+1)-th harmonics of a string fixed at both ends.
1. Understand the relationship between wavelength and harmonic number:
For a string fixed at both ends, the wavelength λ of the n-th harmonic is given by:
λn=2Ln
where L is the length of the string and n is the harmonic number.
2. Set up the equations for the given wavelengths:
For the m-th harmonic, we have:
λm=0.1m
For the (m+1)-th harmonic, we have:
λm+1=0.08m
3. Express the wavelengths in terms of L:
Using the formula for wavelength:
λm=2Lm(1)
λm+1=2Lm+1(2)
4. Substitute the given wavelengths into the equations:
From equation (1):
0.1=2Lm⟹2L=0.1m⟹L=0.1m2=0.05m(3)
From equation (2):
0.08=2Lm+1⟹2L=0.08(m+1)⟹L=0.08(m+1)2=0.04(m+1)(4)
5. Equate the two expressions for L:
From (3) and (4):
0.05m=0.04(m+1)
6. Solve for m:
Expanding the right side:
0.05m=0.04m+0.04
Rearranging gives:
0.05m−0.04m=0.04⟹0.01m=0.04⟹m=0.040.01=4
7. Conclusion:
The value of m is 4.
For a string fixed at both ends, the wavelength λ of the n-th harmonic is given by:
λn=2Ln
where L is the length of the string and n is the harmonic number.
For the m-th harmonic, we have:
λm=0.1m
For the (m+1)-th harmonic, we have:
λm+1=0.08m
Using the formula for wavelength:
λm=2Lm(1)
λm+1=2Lm+1(2)
From equation (1):
0.1=2Lm⟹2L=0.1m⟹L=0.1m2=0.05m(3)
From equation (2):
0.08=2Lm+1⟹2L=0.08(m+1)⟹L=0.08(m+1)2=0.04(m+1)(4)
From (3) and (4):
0.05m=0.04(m+1)
Expanding the right side:
0.05m=0.04m+0.04
Rearranging gives:
0.05m−0.04m=0.04⟹0.01m=0.04⟹m=0.040.01=4
The value of m is 4.
Topper's Solved these Questions
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Matrix Matching
16 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - More Than One Option is Correct
23 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
Similar Questions
A string fastened at both ends has successive resonances with wavelengths of 0.1 m for mth harmonic and 0.08 m for (m+1)th harmonic.
the length of the string is
View SolutionA string fastened at both ends has successive resonances with wavelengths of 0.54 m for nth harmonic and 0.48 m for the (n+1) th harmonic and 0.48 m for the (n+1) th harmonic.
(a) Which harmonics are these?
(b) What is the length of the stirng?
(c) What is the wavelength of the fundamental frequency?
View SolutionA string of length 2m is fixed at two ends. It is in resonance with a tuning fork of frequency 240 Hz in its third harmonic. Then speed of wave sound in string and its fundamental frequency is:
View Solutionm2−m+1=0 find the value of m
View SolutionIf a=1a=manda≠0, find in terms of 'm', the value of :
a−1a
View SolutionIn a GP if the (m+n)th term is p and (m−n)th term is q then mth term is
View SolutionA string 2.0 m long and fixed at its ends is driven by a 240 Hz vibrator. The string vibrates in its third harmonic mode. The speed of the wave and its fundamental frequency is
View Solutionfigure. Shows a student setting up wave wave on a long stretched string. The student's hand makes one complete up and down movement in 0.4s and in each up and down movement the hand moves by a height of 0.3m. The wavelength of the waves on the string is 0.8m.
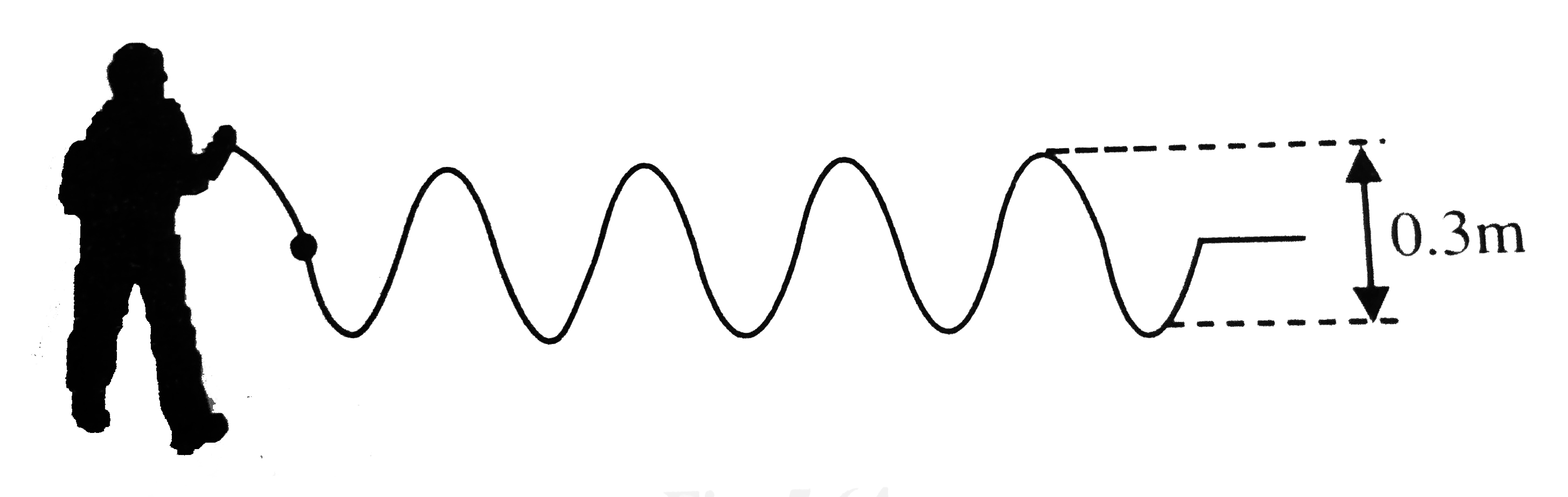
The amplitude of the wave is
View SolutionIn the experinment for the determinnation of the speed of sound in air using the resonance column method, the length of the air column that resonates in the fu ndamental mode , with a tuning fork is 0.1m . When this length is changed to 0.35m , the same tuning fork resonates with the first overtone. Calculate the end correction.
(a) 0.012m
(b) 0.0025m
(c) 0.05m
(d) 0.024m
View SolutionThe equation for the vibration of a string fixed at both ends vibrating in its second harmonic is given by y=2sin(0.3cm−1)xcos((500πs−1)t)cm. The length of the string is :
View Solution
