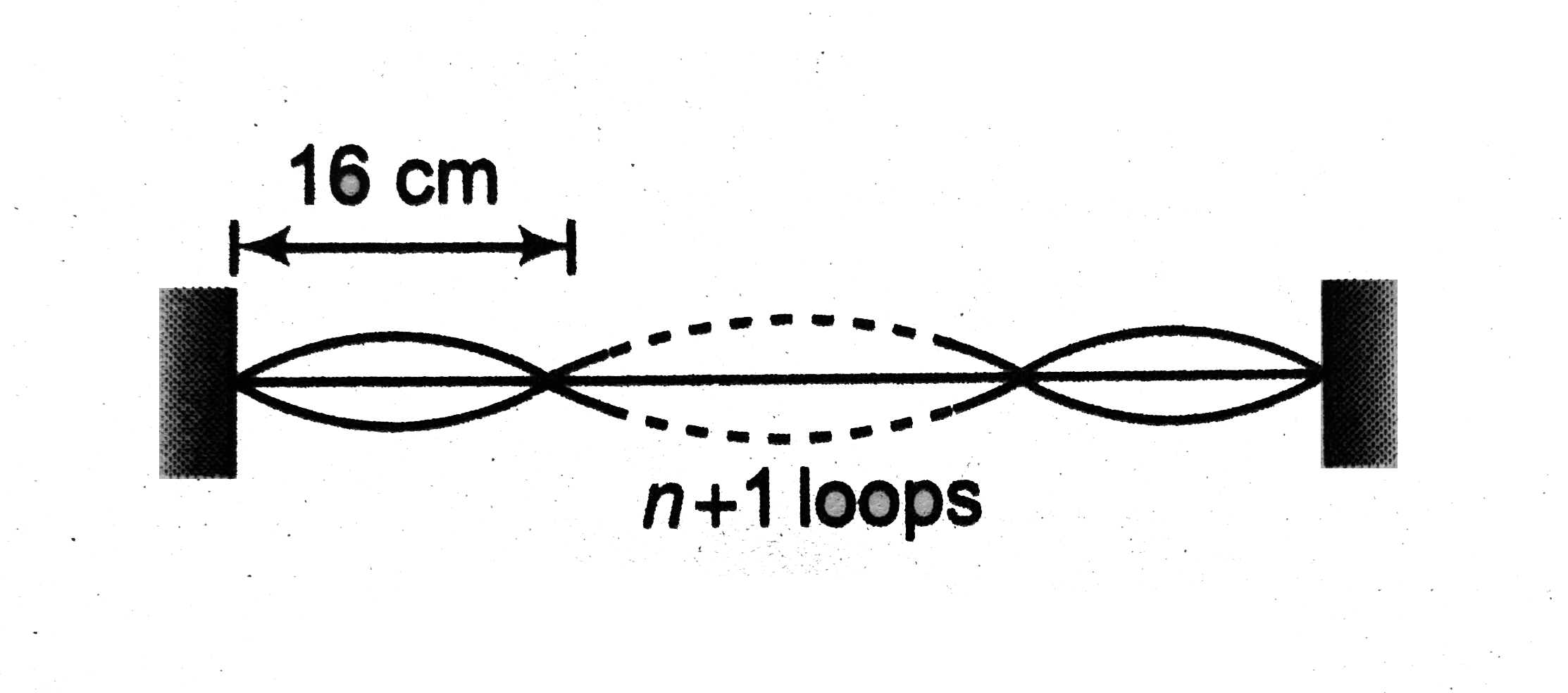
A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm, respectively.
(a) What is the minimum possible length of the string?
(b) If the tension is 10 N and the linear mass density is 4 g/m, what is the fundamental frequency?
The correct Answer is:A, B, C, D
(a) 
Let l be the length of the string. Then,
18n=l ………………(i)
16(n+1)=l…………..(ii)
From Eqs. (i) and (ii), we get
n=8
and l=144 cm
Therefore, the minimum possible length of the string can be 144 cm.
(b) For fundamental frequency, l=λ2
or λ=2l=288cm
=288 m
Speed of wave on the string,
v=√Tμ
=√104×(10−3)=50ms
∴Fundamentalequency,
f=vλ=502.88
=17.36 Hz

Similar Questions
What is maximum possible wavelength of standing waves in 1m long string if it is fixed at both ends
View SolutionA string fixed at both ends vibrates in a resonant mode with a separation of 2.0cm between the consecutive nodes. For the next higher resonants frequecy this separation to 1.6cm. The length of the string is
View Solution
Knowledge Check
A string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm respectively. The minimum possible length of the string (in cm) is:
A144B152C176D200A string fixed at both ends has consecutive standing wave modes for which the distance between adjacent nodes are 18 cm and 16 cm respectively. The length of the string is -
A144 cmB152 cmC176 cmD200 cmThe string fixed at both ends has standing wave nodes for which distance between adjacent nodes is x1. The same string has another standing wave nodes for which distance between adjacent nodes is x2. If l is the length of the string then x2/x1=l(l+2x1). What is the difference in numbers of the loops in the two cases?
A1B2C3D4
A string 1 m long with mass 0.1 g cm−1 is under a tension of 400 N.Find is fundamental frequency of vibration.
View SolutionA string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string.
View SolutionA string fixed at both ends is 8.40m long and has a mass of 0.120kg. It is subjected to a tension of 96.0N and set oscillating. (a) What is the speed of the waves on the string? (b) What is the longest possible wavelength for a standing wave ? (c) Give the frequency of the wave.
View SolutionA uniform string fixed at both ends vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For next higher resonant frequency, this separation is reduced to 1.6 cm. The length of the string is
View SolutionA string fixed at both the ends forms standing waves with node separation of 5 cm. If the velocity of waves travelling in the string is 4 m/s, then the frequency of vibration of the string will be
View Solution
