A string fixed at its both ends vibrates in 5 loops as shown in the figure. The number of nodes and antinodes respectively

5,6
6,5
7,4
4,7
The correct Answer is:B
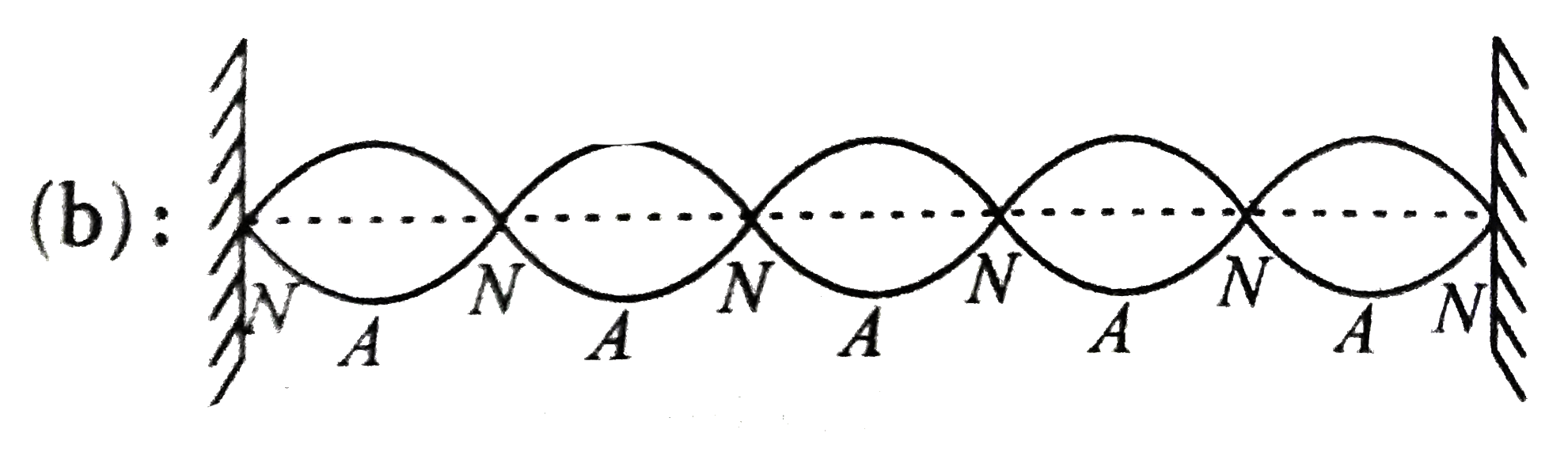
From figure
Total nodes=6
Total antonodes=5
Topper's Solved these Questions
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - Beats
12 Videos
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - Doppler Effect
10 Videos
- WAVESBOOK - NCERT FINGERTIPSCHAPTER - WAVESEXERCISE - The Principle Of Superposition Of Waves
2 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTIPSCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason
15 Videos
Similar Questions
Show that when a string fixed at its two ends vibrates in 1 loops, 2 loops , 3 loops and 4 loops , the frequencies are in the ration 1:2:3:4.
View SolutionA string fixed at both ends vibrates in a resonant mode with a separation of 2.0cm between the consecutive nodes. For the next higher resonants frequecy this separation to 1.6cm. The length of the string is
View Solution
Knowledge Check
A string is vibrating in n loops. The numbers of nodes and anitnodes respectively are
An,nB(n+1),nCn,(n−1)D(n−1),nIn the third normal mode of vibrationn of a closed organ pipe, the number of nodes and antinodes respectively are
A4,3B3,4C3,3D4,4If a string fixed at both ends vibrates in four loops. The wavelength is 10 cm. The length of string is
A5 cmB15 cmC30 cmDNone
When a string fixed at its both ends vibrates in 1 loop, 2 loops, 3 loops and 4 loops, the frequencies are in the ratio
View SolutionIn the fundamental mode of vibration on a stretched string, the number of antinodes are
View SolutionA string fixed at both the ends is vibrating in two segments. The wavelength of the corresponding wave is
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionA taut string at both ends vibrates in its nth overtone. The distance between adjacent node and antinode is found to be 'd'. If the length of the string is L, then
View Solution
